主要是我自己刷题的一些记录过程。如果有错可以指出哦，大家一起进步。
转载代码随想录
原文链接：
代码随想录
leetcode链接：236. 二叉树的最近公共祖先

题目：

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例：

示例 1：

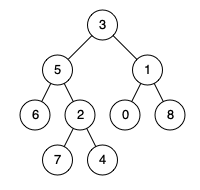
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

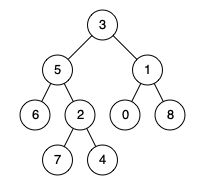
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -10⁹ <= Node.val <= 10⁹
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

思路：

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？

回溯啊，二叉树回溯的过程就是从低到上。

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。

接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。 即情况一：
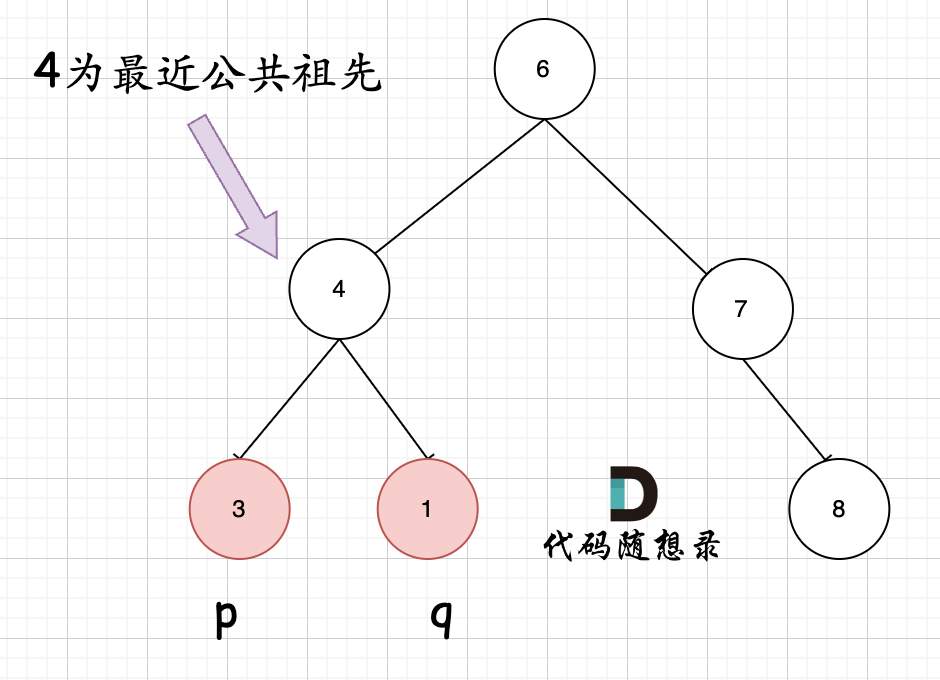判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。

那么有录友可能疑惑，会不会左子树 遇到q 返回，右子树也遇到q返回，这样并没有找到 q 和p的最近祖先。

这么想的录友，要审题了，题目强调：二叉树节点数值是不重复的，而且一定存在 q 和 p。

但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q§。 情况二：
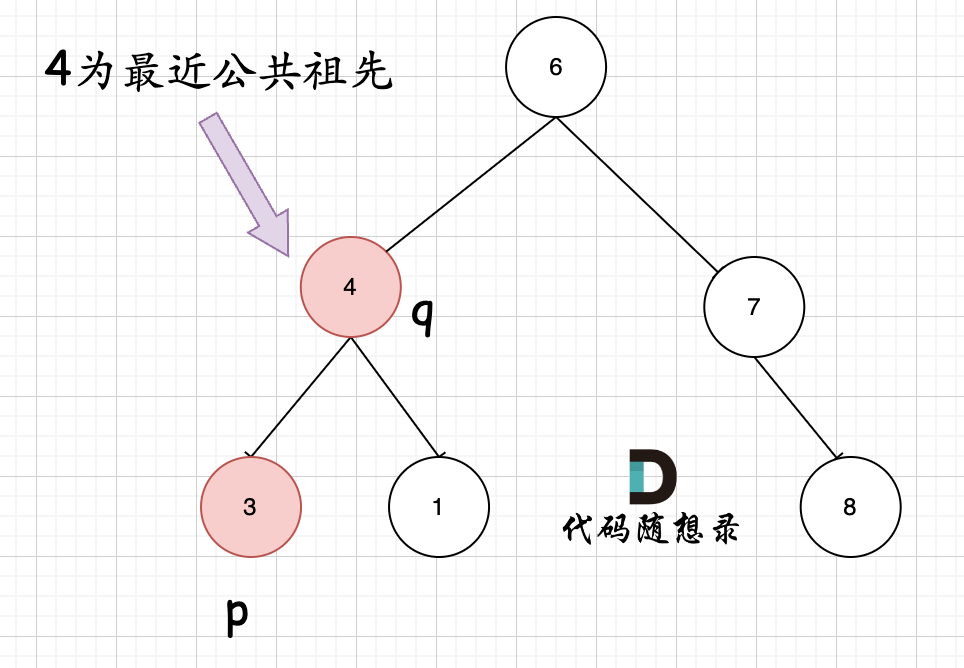其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。

因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。

这一点是很多录友容易忽略的，在下面的代码讲解中，可以再去体会。

递归三部曲：

1.确定递归函数返回值以及参数

需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。

但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

代码如下：

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)

2.确定终止条件

遇到空的话，因为树都是空了，所以返回空。

那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点的处理逻辑，下面讲解。

代码如下：

if (root == q || root == p || root == NULL) return root;

3.确定单层递归逻辑

值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？中说了 递归函数有返回值就是要遍历某一条边，但有返回值也要看如何处理返回值！

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

看出区别了没？

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

如图：
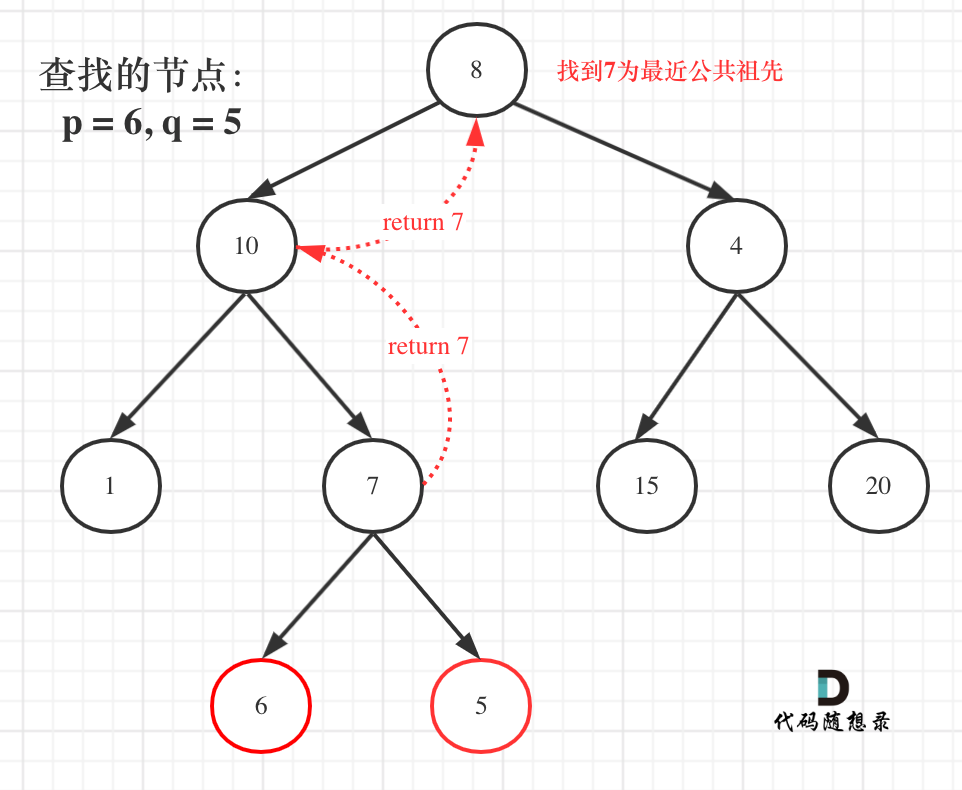就像图中一样直接返回7，多美滋滋。

但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

所以此时大家要知道我们要遍历整棵树。知道这一点，对本题就有一定深度的理解了。

那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解
如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？
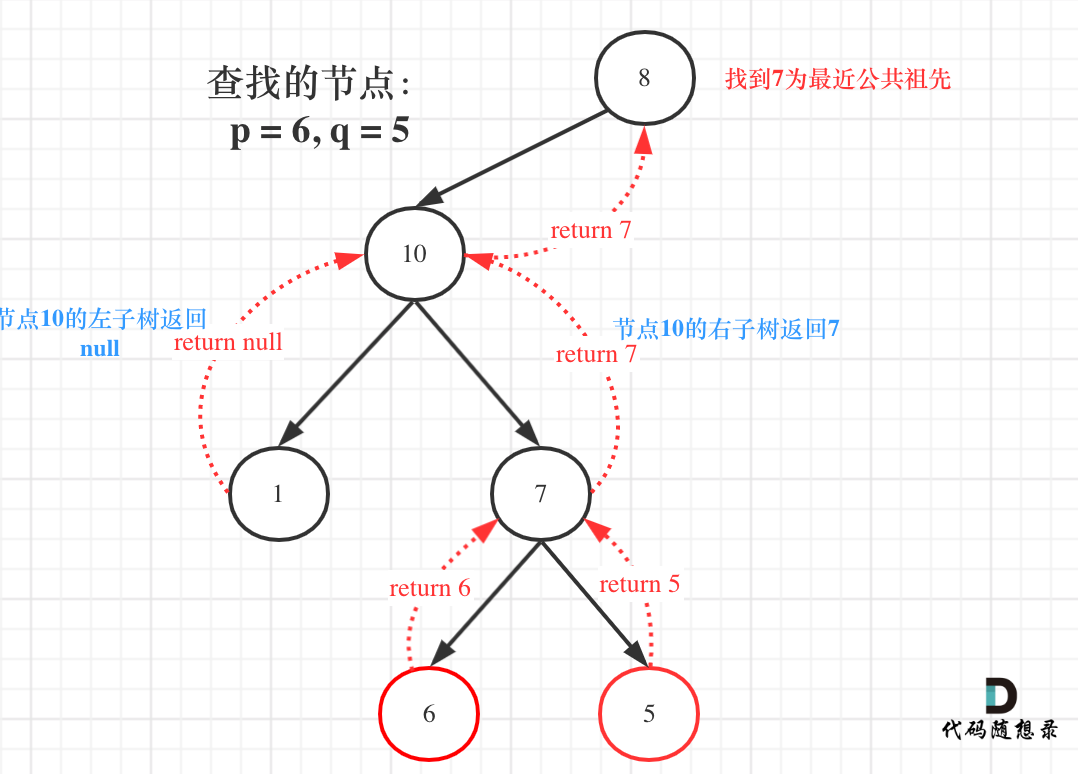图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

代码如下：

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else  { //  (left == NULL && right == NULL)
    return NULL;
}

那么寻找最小公共祖先，完整流程图如下
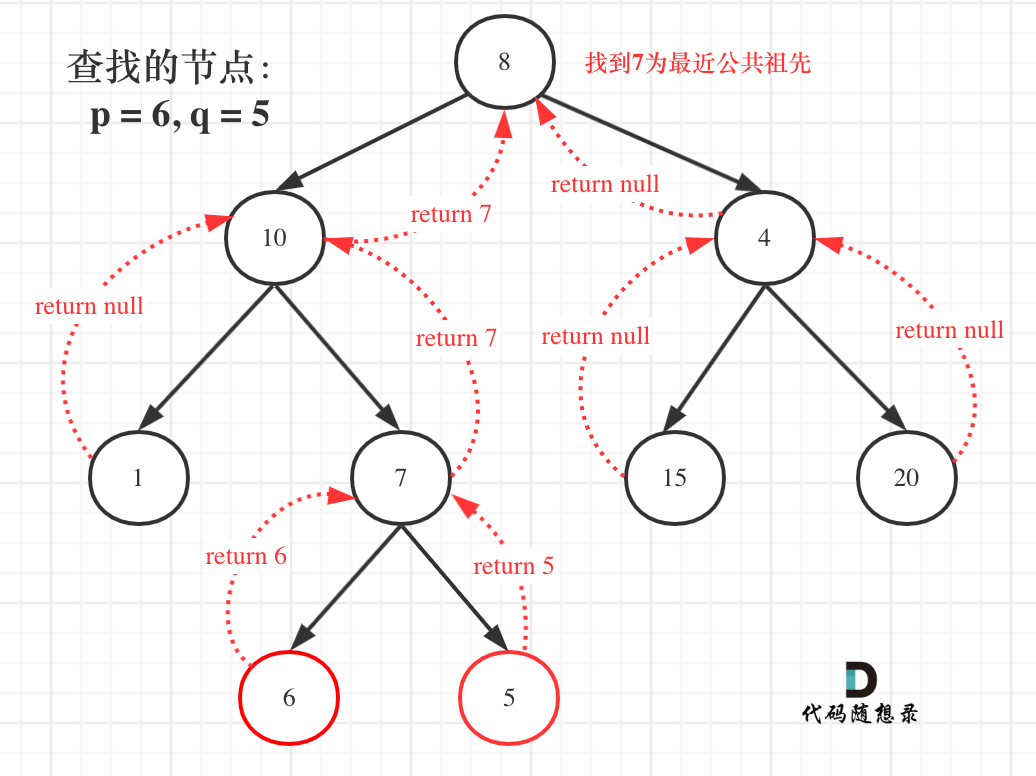从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！

整体代码如下：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == q || root == p || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) return root;

        if (left == NULL && right != NULL) return right;
        else if (left != NULL && right == NULL) return left;
        else  { //  (left == NULL && right == NULL)
            return NULL;
        }
    }
};

稍加精简，代码如下：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == q || root == p || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) return root;
        if (left == NULL) return right;
        return left;
    }
};

这道题目刷过的同学未必真正了解这里面回溯的过程，以及结果是如何一层一层传上去的。

那么我给大家归纳如下三点：

• 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
• 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
• 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。
本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。

自己的代码

我自己的想法就没他这么简单，我是使用了两个vector记录找到p和q的路径，在遍历这两个路径，直到路径不相等就退出从何得到结果。

class Solution {
	vector<vector<TreeNode*>> result1;
	vector<vector<TreeNode*>> result2;
	void searchTree(TreeNode* root, const TreeNode* p, const TreeNode* q, vector<TreeNode*>& path) {
		if (!root) return;	//前序遍历

		path.push_back(root);
		if (root == p) result1.push_back(path);
		if (root == q) result2.push_back(path);
		if (root->left) {
			searchTree(root->left, p, q, path);
			path.pop_back();
		}

		if (root->right) {
			searchTree(root->right, p, q, path);
			path.pop_back();
		}
	}

public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		vector<TreeNode*> path;
		searchTree(root, p, q, path);
		TreeNode* result=nullptr;
		int size = result1[0].size() < result2[0].size() ? result1[0].size() : result2[0].size();
		for (int i = 0; i < size; ++i) {
			if (result1[0][i] == result2[0][i]) result = result2[0][i];
			else break;
		}
		return result;
	}
};