通配符之设定类型通配符的上限-------什么时候需要设置上限????协变

还差一个Canvas类

这样定义行不行?不行!!!
测试一下:

注意上面的drawAll()方法的形参类型是List , 而List

那就可以改写一下:

将Canvas改为如上形式,就可以把List
List<? extends Shape>是受限制通配符的例子,此处的问号(?)代表一个未知的类型,就像前面看到的通配符一样。但是此处的这个未知类型一定是Shape的子类型(也可以是Shape本身),因此可以把Shape称为这个通配符的上限(upper bound)。
类似地,由于程序无法确定这个受限制的通配符的具体类型,所以不能把Shape对象或其子类的对象加入这个泛型集合中。例如,下面代码就是错误的。

与使用普通通配符相似的是,shapes.add()的第二个参数类型是?extends Shape,它表示Shape未知的子类,程序无法确定这个类型是什么,所以无法将任何对象添加到这种集合中。
简而言之,这种指定通配符上限的集合,只能从集合中取元素 (取出的元素总是上限的类型或其子类),不能向集合中添加元素(因为编译器没法确定集合元素实际是哪种子类型)。
对于更广泛的泛型类来说,指定通配符上限就是为了支持类型型变。比如Foo是Bar的子类,这样A就相当于A<? extends Bar>的 子类,可以将A赋值给A<? extends Bar>类型的变量,这种型变方式被称为协变。
对于协变的泛型而言,它只能调用泛型类型作为返回值类型的方法(编译器会将该方法返回值当成通配符上限的类型);而不能调用泛型类型作为参数的方法。口诀是:协变只出不进!
提示:
没有指定通配符上限的泛型类,相当于通配符上限是Object。
那么反过来讲,有下限?有!!!
通配符之设定类型通配符的下限-------什么时候需要设置下限????逆变
通配符的下限用<? super类型>的方式来指定,通配符下限的作用与通配符上限的作用恰好相反。指定通配符的下限就是为了支持类型型变。比如Foo是Bar的子类,当程序需要一个A<? super Foo>变量时,程序可以将A、A赋值给A<? super Foo>类型的变量,这种型变方式被称为逆变。
对于逆变的泛型集合来说,编译器只知道集合元素是下限的父类型,但具体是哪种父类型则不确定。因此,这种逆变的泛型集合能向其中添加元素(因为实际赋值的集合元素总是逆变声明的父类),从集合中取元素时只能被当成Object类型处理(编译器无法确定取出的到底是哪个父类的对象)。
对于逆变的泛型而言,它只能调用泛型类型作为参数的方法;而不能调用泛型类型作为返回值类型的方法。口诀是:逆变只进不出!
假设自己实现一个工具方法:
实现将src集合中的元素复制到dest集合的功能,因为dest集合可以保存src集合中的所有元素,所以dest集合元素的类型应该是src集合元素类型的父类。对于复制方法,可以这样理解两个集合参数之间的依赖关系:不管src集合元素的类型是什么,只要dest集合元素的类型与前者相同或者是前者的父类即可,此时通配符的下限就有了用武之地。下面程序采用通配符下限的方式来实现该copy()方法。

使用这种语句,就可以保证程序的①处调用后推断出最后一个被复制的元素类型是Integer,而不是笼统的Number类型。
引申:
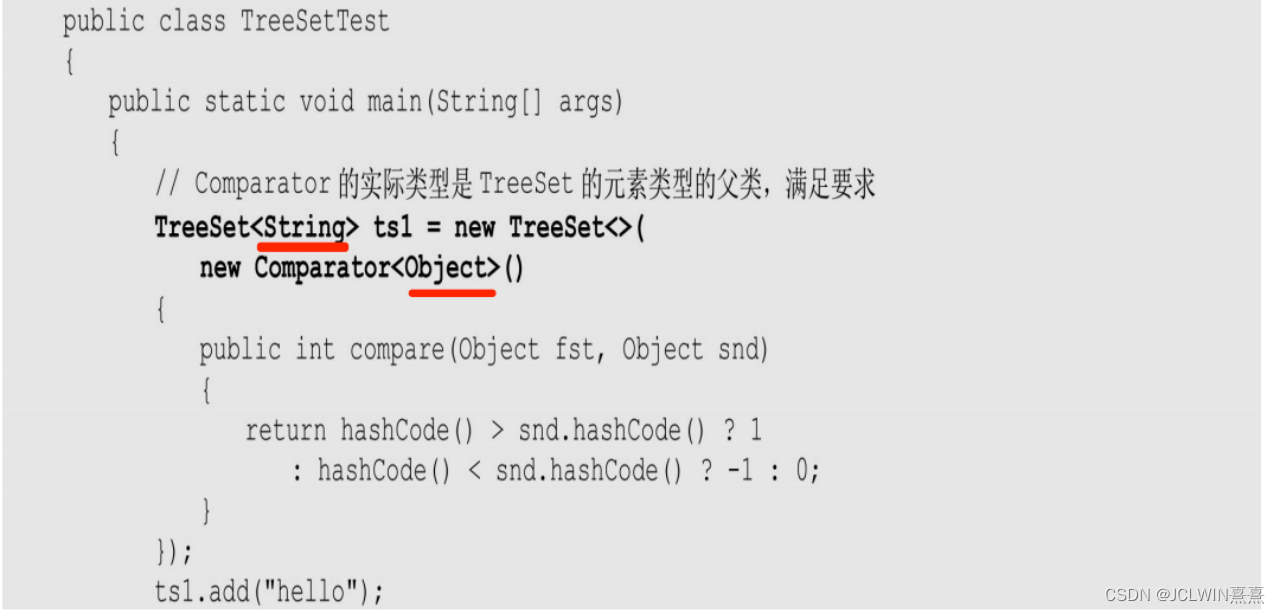
Java集合框架中的TreeSet有一个构造器也用到了这种设定通配符下限的语法。

TreeSet会对集合中的元素按自然顺序或定制顺序进行排序。如果需要TreeSet对集合中的所有元素进行定制排序,则要求TreeSet对象有一个与之关联的Comparator对象。上面构造器中的参数c就是进行定制排序的Comparator对象。
同时其实Comparator接口也是一个带泛型声明的接口:

通过这种带下限的通配符的语法,可以在创建TreeSet对象时灵活地选择合适的Comparator。假定需要创建一个TreeSet集合,并传入一个可以比较String大小的Comparator,这个Comparator既可以是Comparator,也可以是Comparator—只要尖括号里传入的类型是String的父类型(或它本身)即可。