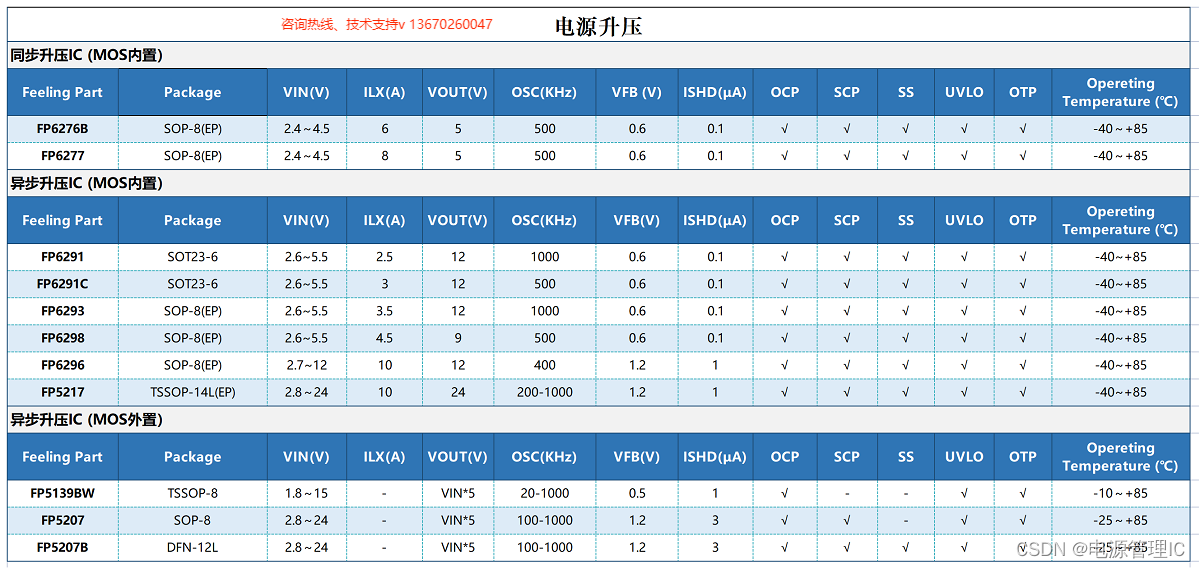
目录
详细布置:
1. 309. 买卖股票的最佳时机含冷冻期
2. 714. 买卖股票的最佳时机含手续费
详细布置:
1. 309. 买卖股票的最佳时机含冷冻期
给定一个整数数组
prices,其中第prices[i]表示第i天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
其实本题很多同学搞的比较懵,是因为出现冷冻期之后,状态其实是比较复杂度,例如今天买入股票、今天卖出股票、今天是冷冻期,都是不能操作股票的。
具体可以区分出如下四个状态:
- 状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
- 不持有股票状态,这里就有两种卖出股票状态
- 状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
- 状态三:今天卖出股票
- 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
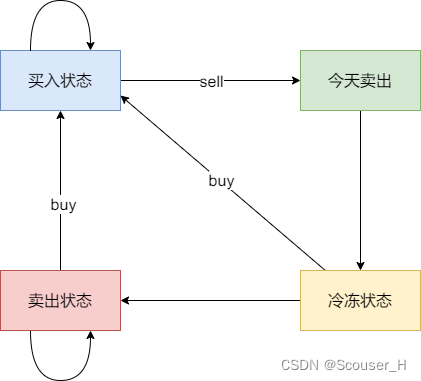
很多题解为什么讲的比较模糊,是因为把这四个状态合并成三个状态了,其实就是把状态二和状态四合并在一起了。
从代码上来看确实可以合并,但从逻辑上分析合并之后就很难理解了
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n == 0:
return 0
dp = [[0] * 4 for _ in range(n)] # 创建动态规划数组,4个状态分别表示持有股票、不持有股票且处于冷冻期、不持有股票且不处于冷冻期、不持有股票且当天卖出后处于冷冻期
dp[0][0] = -prices[0] # 初始状态:第一天持有股票的最大利润为买入股票的价格
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i]) # 当前持有股票的最大利润等于前一天持有股票的最大利润或者前一天不持有股票且不处于冷冻期的最大利润减去当前股票的价格
dp[i][1] = max(dp[i-1][1], dp[i-1][3]) # 当前不持有股票且处于冷冻期的最大利润等于前一天持有股票的最大利润加上当前股票的价格
dp[i][2] = dp[i-1][0] + prices[i] # 当前不持有股票且不处于冷冻期的最大利润等于前一天不持有股票的最大利润或者前一天处于冷冻期的最大利润
dp[i][3] = dp[i-1][2] # 当前不持有股票且当天卖出后处于冷冻期的最大利润等于前一天不持有股票且不处于冷冻期的最大利润
return max(dp[n-1][3], dp[n-1][1], dp[n-1][2]) # 返回最后一天不持有股票的最大利润
2. 714. 买卖股票的最佳时机含手续费
给定一个整数数组
prices,其中prices[i]表示第i天的股票价格 ;整数fee代表了交易股票的手续费用。你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
相对于动态规划:122.买卖股票的最佳时机II (opens new window),本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
唯一差别在于递推公式部分,所以本篇也就不按照动规五部曲详细讲解了,主要讲解一下递推公式部分。
这里重申一下dp数组的含义:
dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
所以:dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金,注意这里需要有手续费了即:dp[i - 1][0] + prices[i] - fee
所以:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
本题和动态规划:122.买卖股票的最佳时机II (opens new window)的区别就是这里需要多一个减去手续费的操作。
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n)]
dp[0][0] = -prices[0] #持股票
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)
return max(dp[-1][0], dp[-1][1])