重温被Mamba带火的SSM：HiPPO的一些遗留问题

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

书接上文，在上一篇文章《重温被Mamba带火的SSM：线性系统和HiPPO矩阵》中，我们详细讨论了 HiPPO 逼近框架其 HiPPO 矩阵的推导，其原理是通过正交函数基来动态地逼近一个实时更新的函数，其投影系数的动力学正好是一个线性系统，而如果以正交多项式为基，那么线性系统的核心矩阵我们可以解析地求解出来，该矩阵就称为 HiPPO 矩阵。

当然，上一篇文章侧重于 HiPPO 矩阵的推导，并没有对它的性质做进一步分析，此外诸如“如何离散化以应用于实际数据”、“除了多项式基外其他基是否也可以解析求解”等问题也没有详细讨论到。接下来我们将补充探讨相关问题。

离散格式

假设读者已经阅读并理解上一篇文章的内容，那么这里我们就不再进行过多的铺垫。在上一篇文章中，我们推导出了两类线性 ODE 系统，分别是：

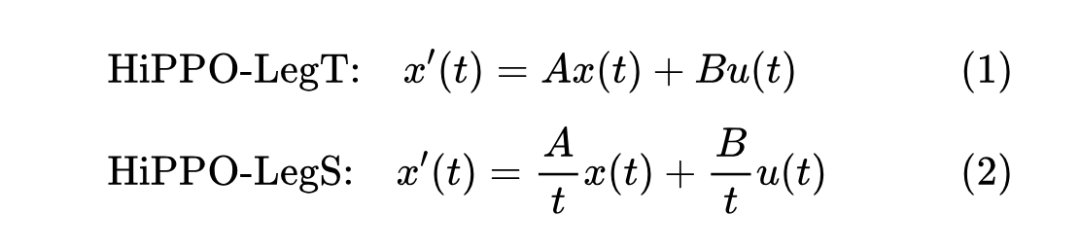
其中是与时间无关的常数矩阵，HiPPO 矩阵主要指矩阵。在这一节中，我们讨论这两个 ODE 的离散化。

输入转换

在实际场景中，输入的数据点是离散的序列，比如流式输入的音频信号、文本向量等，我们希望用如上的 ODE 系统来实时记忆这些离散点。为此，我们先定义

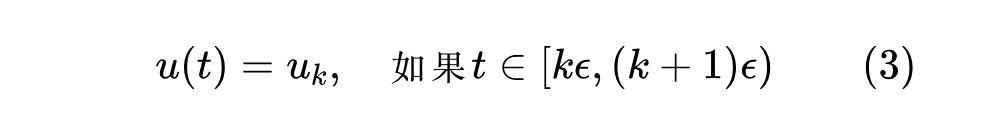
其中就是离散化的步长。该定义也就是说在区间内，是一个常数函数，其值等于。很明显这样定义出来的无损原本序列的信息，因此记忆就相当于记忆序列。

从变换到，可以使得输入信号重新变回连续区间上的函数，方便后面进行积分等运算，此外在离散化的区间内保持为常数，也能够简化离散化后的格式。

LegT版本

我们先以 LegT 型 ODE（1）为例，将它两端积分

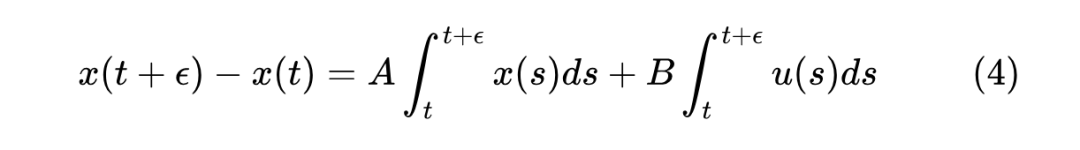
其中。根据的定义，它在区间内恒为，于是的积分可以直接算出来：

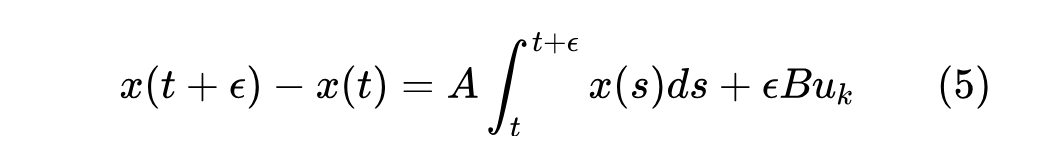
接下来的结果，就取决于我们如何近似的积分了。假如我们认为在区间内近似恒等于，那么就得到前向欧拉格式

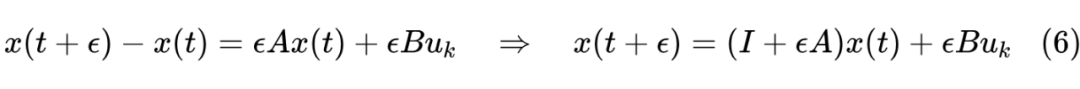
我们认为在区间内近似恒等于，那么就得到后向欧拉格式

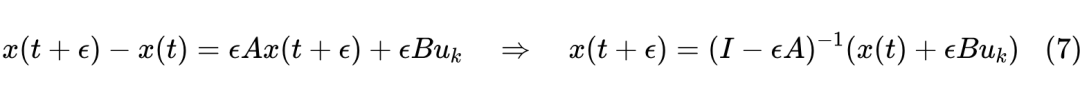
前后向欧拉都具有相同的理论精度，但后向通常会有更好的数值稳定性。如果要更准确一些，那么认为在区间内近似恒等于，那么得到双线性形式：

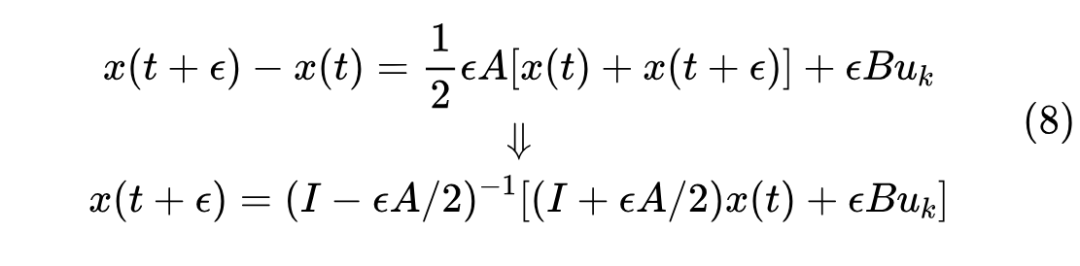
这也等价于先用前向欧拉走半步，再用后向欧拉走半步。更一般地，我们还可以认为在区间内近似恒等于，其中，这就不进一步展开了。事实上，我们也可以完全不做近似，因为结合式（1）以及在区间中是常数，我们完全可以用“常数变易法” [1] 来精确求解出来，结果是

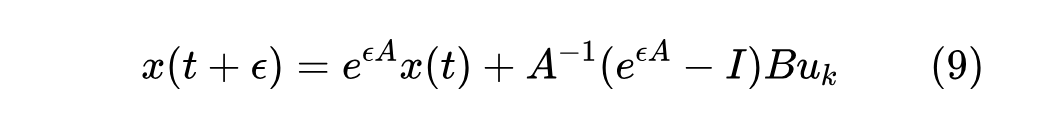
这里的矩阵指数按照级数来定义，可以参考《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》[2]。

LegS版本

现在轮到 LegS 型 ODE 了，它的思路跟 LegT 型基本一致，结果也大同小异。首先将式（2）两端积分得到

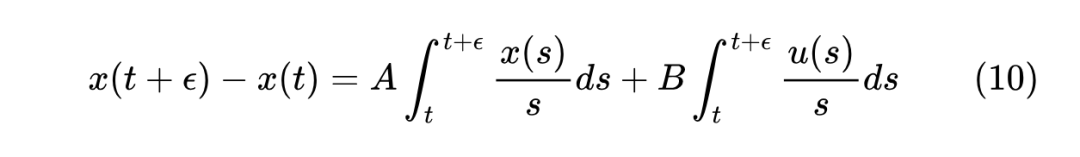
根据定义，第二项积分的在恒为，所以它相当于的积分，可以直接积分出来得，当然直接换为一阶近似也无妨，因为本身到的变换有很大自由度，这点误差无所谓。至于第一项积分，我们直接采用精度更高的中点近似，得到

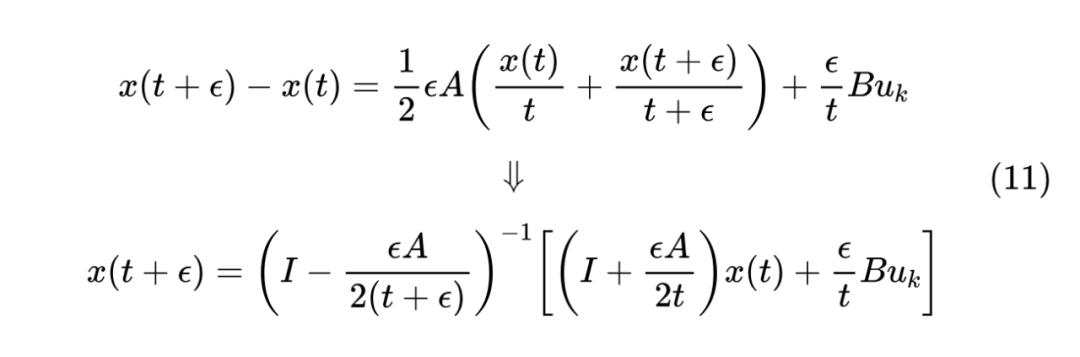
事实上，式（2）也可以精确求解，只需要留意到它等价于

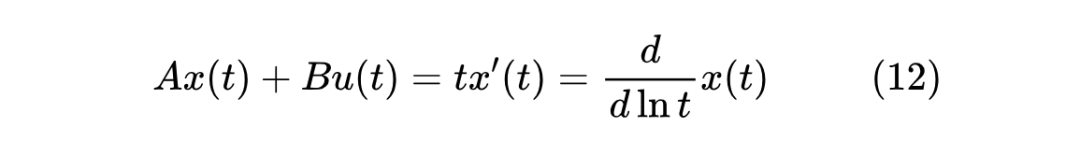
这意味着只需要做变量代换，那么 LegS 型 ODE 就可以转化为 LegT 型 ODE：

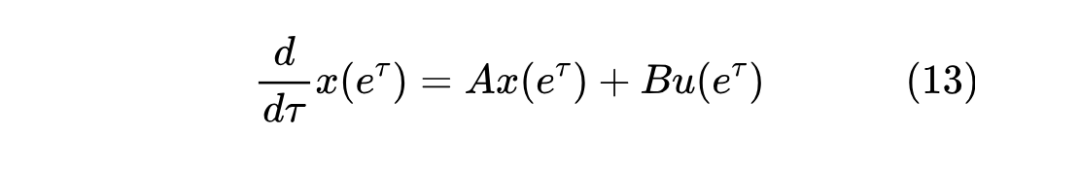
利用式（9）得到（由于变量代换，时间间隔由变成）

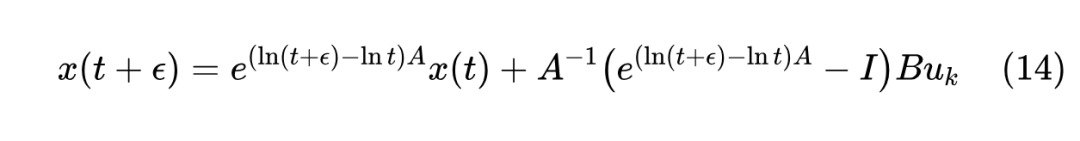
然而，上式虽然是精确解，但不如同为精确解的式（9）好用，因为式（9）的指数矩阵部分是，跟时间无关，所以一次性计算完就可以了。但上式中在矩阵指数里边，意味着在迭代过程中需要反复计算矩阵指数，对计算并不友好，所以 LegS 型 ODE 我们一般只会用式（11）来离散化。

优良性质

接下来，LegS 是我们的重点关注对象。重点关注 LegS 的原因并不难猜，因为从推导的假设来看，它是目前求解出来的唯一一个能够记忆整个历史的 ODE 系统，这对于很多场景如多轮对话来说至关重要。此外，它还有其他的一些比较良好且实用的性质。

尺度不变

比如，LegS 的离散化格式（11）是步长无关的，我们只需要将代入里边，并记，就可以发现

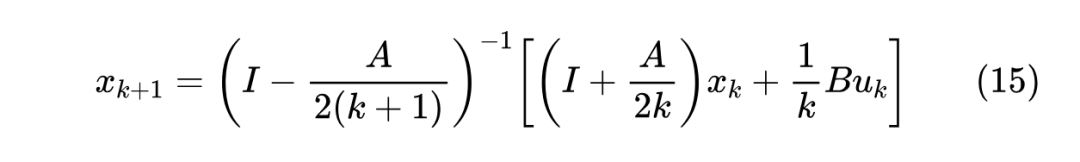
步长被自动地消去了，从而自然地减少了一个需要调的超参数，这对于炼丹人士显然是一个好消息。注意步长无关是 LegS 型 ODE 的一个固有性质，它跟具体的离散化方式并无直接关系，比如精确解（14）同样是步长无关的：

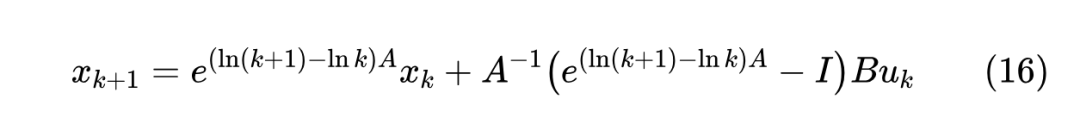
其背后的原因，在于 LegS 型 ODE 满足“时间尺度不变性（Timescale equivariance）”——如果我们设代入 LegS 型 ODE，将得到

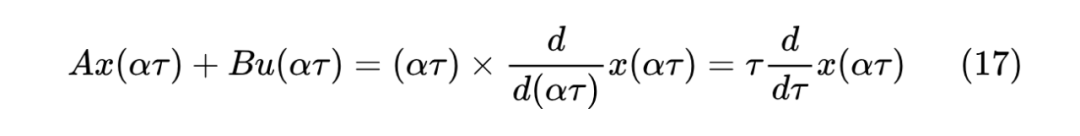
这意味着，当我们将换成时，LegS 的 ODE 形式并没有变化，而对应的解则是换成了。这个性质的直接后果就是：当我们选择更大的步长时，递归格式不需要发生变化，因为结果的步长也会自动放大，这就是 LegS 型 ODE 离散化与步长无关的本质原因。

长尾衰减

LegS 型 ODE 的另一个优良性质是，它关于历史信号的记忆是多项式衰减（Polynomial decay）的，这比常规 RNN 的指数衰减更缓慢，从而理论上能记忆更长的历史，更不容易梯度消失。为了理解这一点，我们可以从精确解（16）出发，从式（16）可以看到，每递归一步，历史信息的衰减效应可以用矩阵指数来描述，那么从第步递归到第步，总的衰减效应是

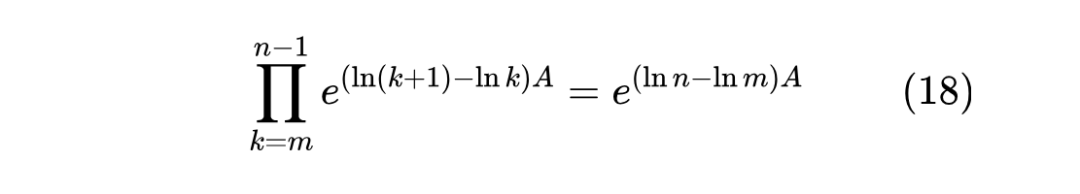
回顾 HiPPO-LegS 中的形式：

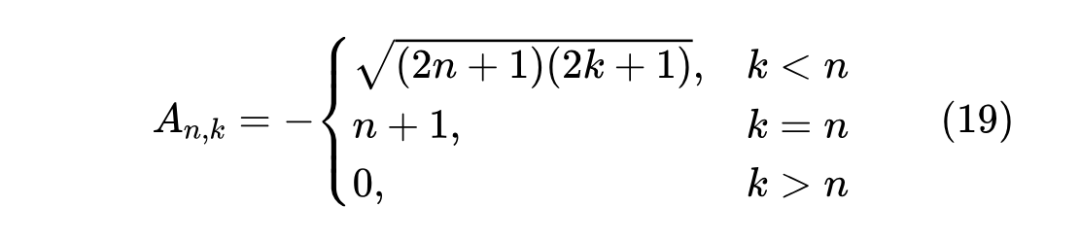
从定义可以看出，是一个下三角阵，其对角线元素为。我们知道，三角阵的对角线元素正好是它的特征值（参考 Triangular matrix [3]），由此可以看到一个大小的矩阵，有个不同的特征值，这说明矩阵是可对角化的，即存在可逆矩阵，使得，其中，于是我们有

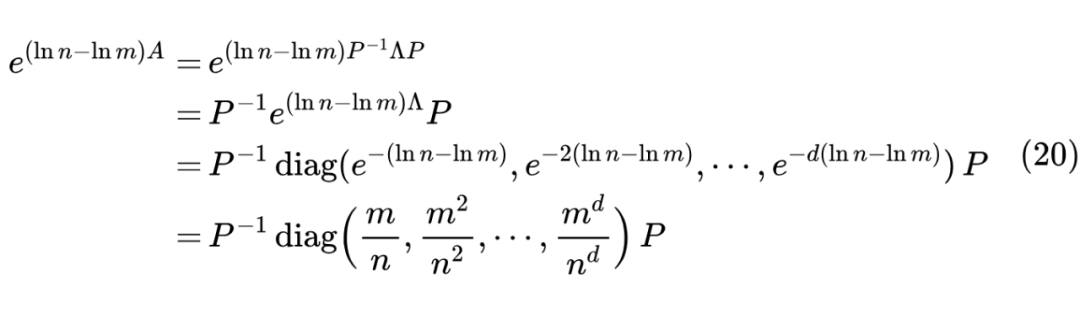
可见，最终的衰减函数是的次函数的线性组合，所以 LegS 型 ODE 关于历史记忆至多是多项式衰减的，比指数衰减更加长尾，因此理论上有更好的记忆力。

计算高效

最后，我们指出 HiPPO-LegS 的矩阵是计算高效（Computational efficiency）的。具体来说，直接按照矩阵乘法的朴素实现的话，一个的矩阵乘以的列向量，需要做次乘法，但 LegS 的矩阵与向量相乘则可以降低到次，更进一步地，我们还可以证明离散化后的（11）也可以在完成。

为了理解这一点，我们首先将 HiPPO-LegS 的 A 矩阵等价地改写成

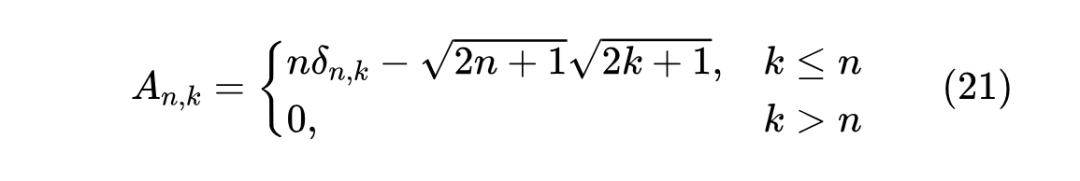
对于向量，我们有

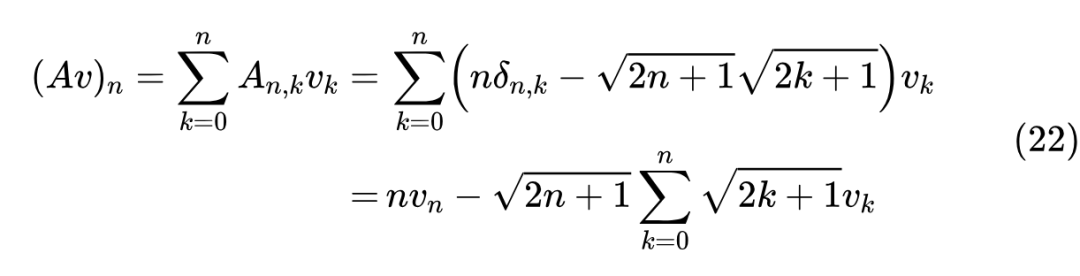
这包含三种运算，第一项的是向量与做逐位相乘运算，第二项的则是向量与做逐位相乘，然后就是运算，最后乘以就是再逐位相乘向量，每一步都可以在内完成，因此总的复杂度是的。

我们再来看（11），它包含两步“矩阵-向量”乘法运算，一是，是任意实数，刚才我们已经证明了是计算高效的，自然也是；二是，接下来我们将证明它也是计算高效的。这只需要留意到求等价于解方程，利用上面给出的表达式，我们可以得到

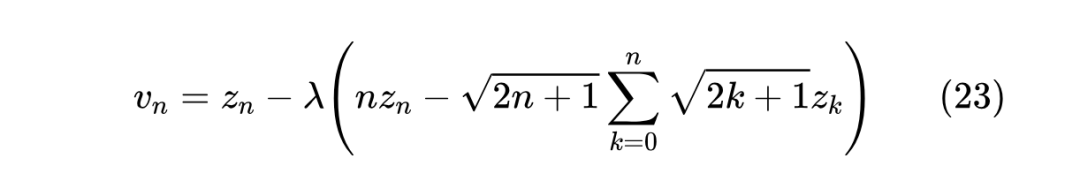
记，那么，代入上式得

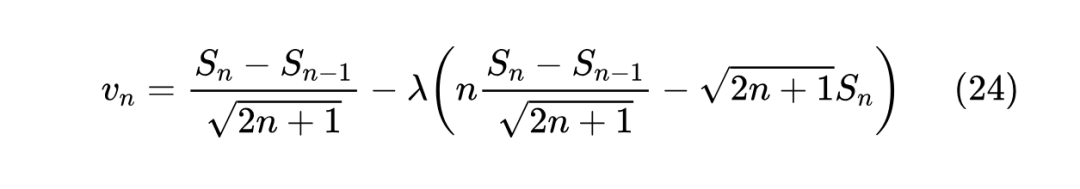
整理得

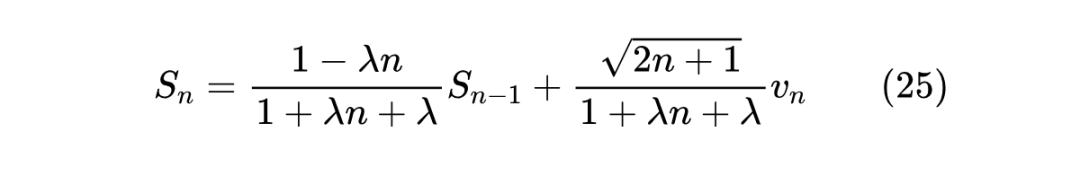
这是一个标量的递归式，可以完全串行地计算，也可以利用 Prefix Sum 的相关算法并行计算（参考这里），计算复杂度为或者，总之相比都会更加高效。

傅立叶基

最后，我们以傅立叶基的一个推导收尾。在上一篇文章中，我们以傅立叶级数来引出了线性系统，但只推导了邻近窗口形式的结果，而后面的勒让德多项式基我们则推导了邻近窗口和完整区间两个版本（即 LegT 和 LegS）。那么傅立叶基究竟能不能推导一个跟 LegS 相当的版本呢？其中会面临什么困难呢？下面我们对此进行探讨。

同样地，相关铺垫我们不再重复，按照上一节的记号，傅立叶基的系数为

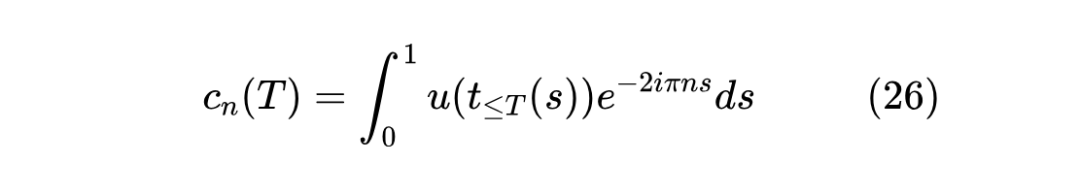
跟 LegS 一样，为了记忆整个区间的信号，我们需要一个的映射，为此选取最简单的，代入后两边求导得到

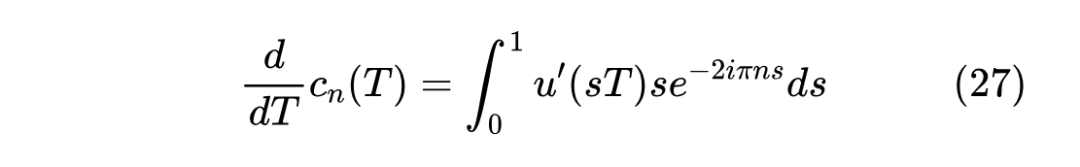
分部积分得到

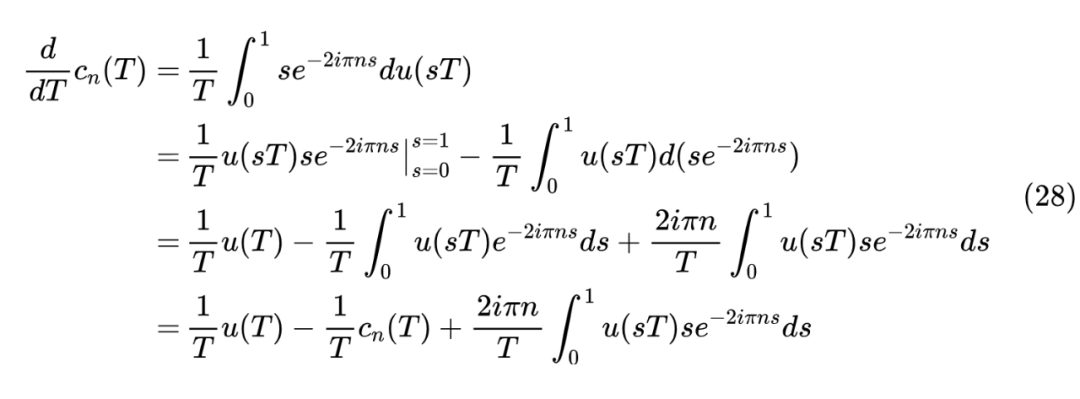
上一篇文章我们提到，HiPPO 选取勒让德多项式为基的重要原因之一是可以分解为的线性组合，而傅里叶基的则不能做到这一点。但事实上，如果允许误差的话，这个断论是不成立的，因为我们同样可以将分解为傅里叶级数：

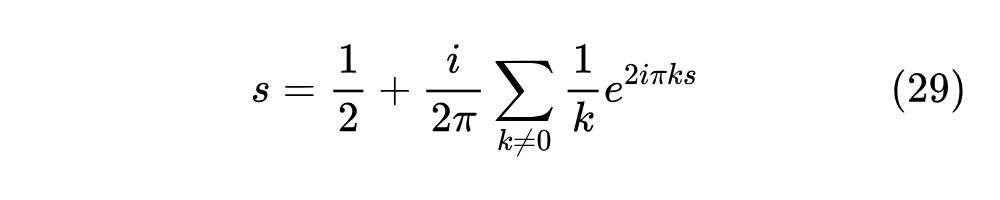
这里的求和有无限项，如果要截断为有限项的话，就会产生误差，但我们可以先不纠结这一点，直接往上代入得到

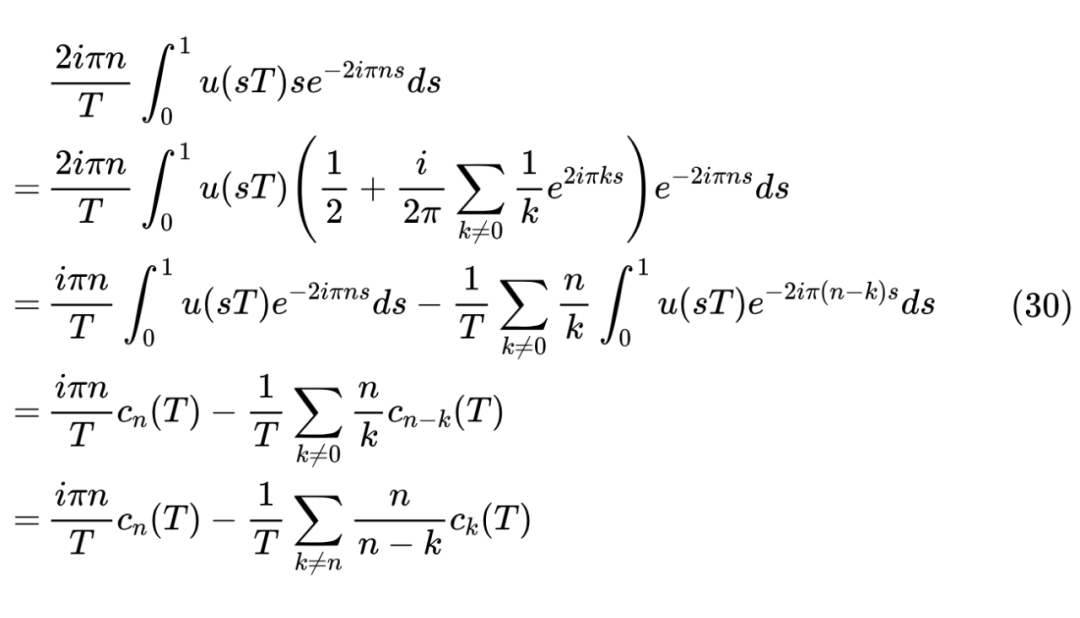
这样一来

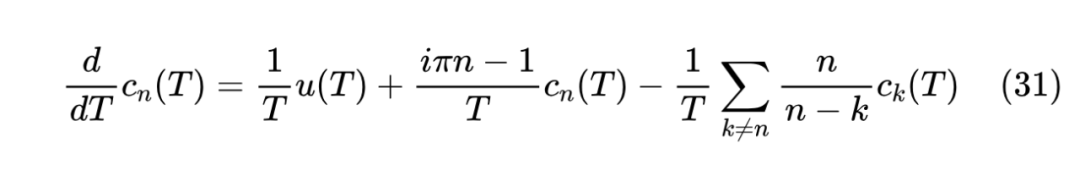
所以可以写出

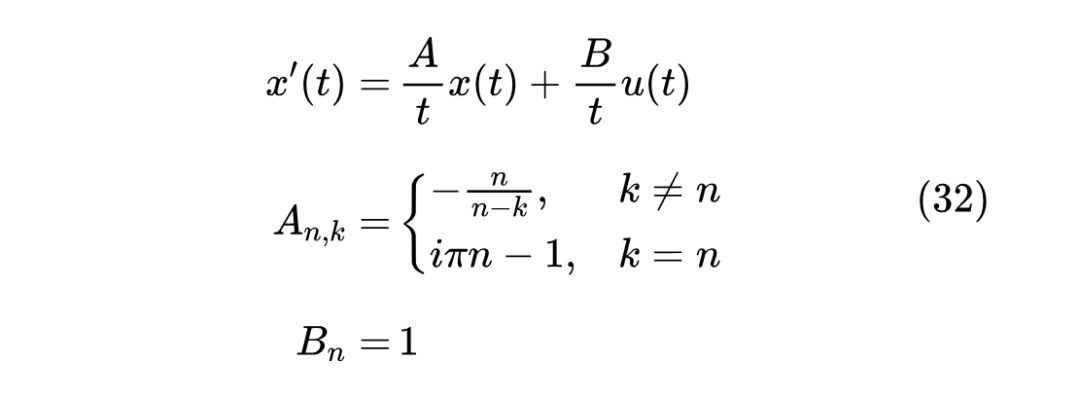
实际使用的时候，我们只需要截断，就可以得到一个的矩阵。截断带来的误差其实是无所谓的，因为我们在推导 HiPPO-LegT 的时候同样引入了有限级数近似，那会我们同样也没考虑误差，或者反过来讲，对于特定的任务，我们会选择适当的规模（即 N 的大小），而这个“适当”的含义之一，就是截断带来误差对于该任务是可以忽略的。

对大多数人来说，傅立叶基的这个推导可能还更容易理解一些，因为勒让德多项式对很多读者来说都比较陌生，尤其是 LegT、LegS 推导过程中用到的几个恒等式，而对于傅立叶级数大多数读者应该或多或少都有所了解。

不过，从结果上来看，傅立叶基的这个结果可能不如 LegS 实用，一来它引入了复数，这增加了实现的复杂度，二来它推导出的 A 矩阵不像 LegS 那样是个相对较淡的下三角阵，因此理论分析起来也更为复杂。所以，大家权当它是一道深化对 HiPPO 的理解的练习题就好。