模型评估*

数据集的切割

训练-测试数据的方式、交叉验证的方式

我们通常会把数据集切割为训练数据集或者测试数据集，训练数据集用来训练模型用，测试数据集我们一般用来测试模式的实际效能怎么样。

我们在将数据分为训练和测试数据集的时候我们会使用分层抽样的方法来进行。

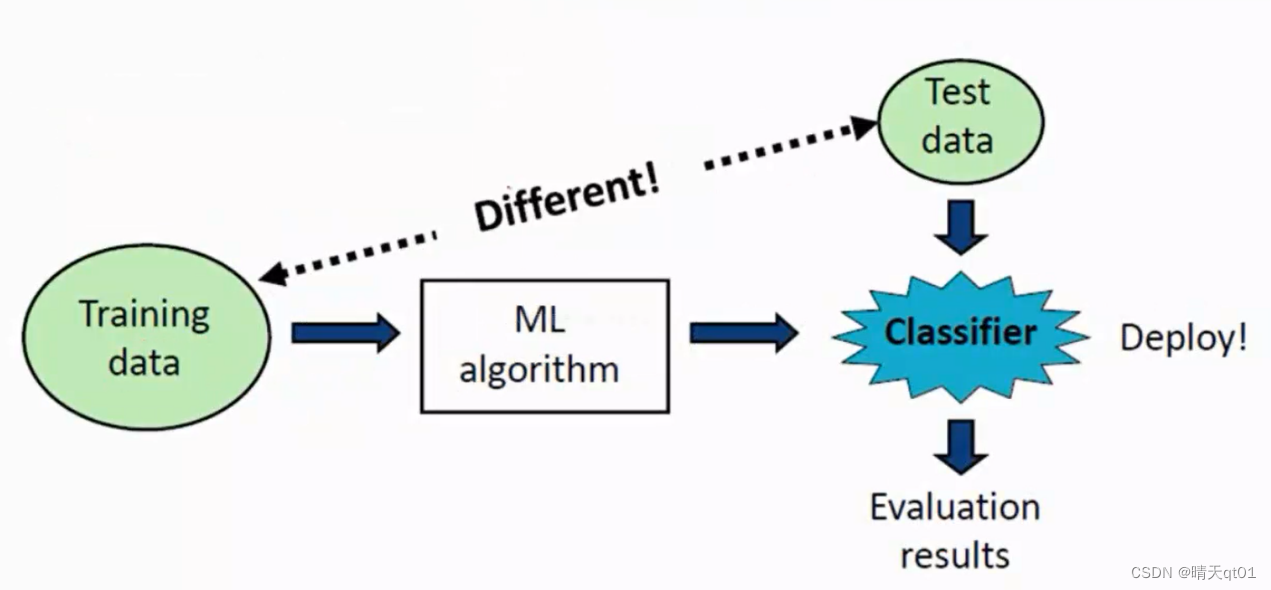
通常我们会拿训练数据通过机器学习的算法，产生我们的分类器，模型，然后我们再利用另外一笔数据来测试模型来得到我们的评估结果，如果这个结果还不错，我们就可以将这个模型实际上线使用，如果结果不好，我们要对数据进行修正，或者对数据集进行新的处理。

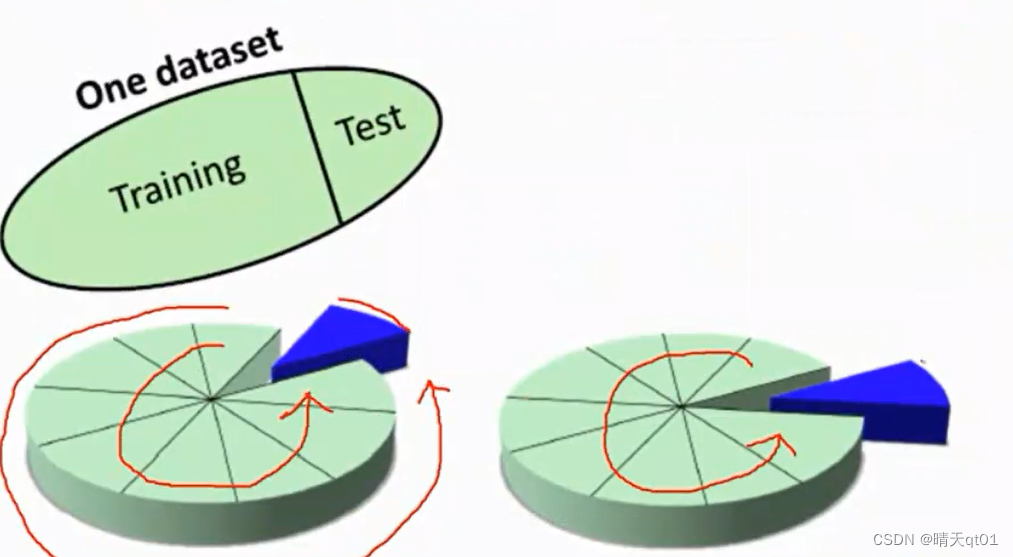
测试数据和训练数据必须是不同的，但是我们平时都是只有一个数据集，这时我们应该怎么办，我们就需要对数据进行切割为训练和测试两个部分。这两个部分就不会有重叠。所以这边我们就要使用不可取回式的随机样方法得到二者。

怎么样将数据随机抽样为训练数据集和测试数据集。假设我们选择有1000笔数据，我个人的习惯会把其中的百分之80当做训练数据，百分之20当做测试数据，其他比例当然也可以

训练数据：可以做任何的分析处理。

测试数据：不能做任何的分析处理。

测试数据是要表示为原始数据。不过我们很多做数据挖掘竞赛的，参赛者经常都会拿测试数据集去做分析，其实这样不好，但是有时候，我们会去看看测试数据集的分布，借用我们从测试数据集看到的现象来调整我们的训练数据集，

我们举个简单的例子。比如我们发现测试数据中性别全部都是女生这时我们的训练数据集就可以把男生全部筛除掉，我们就把女生进行建模，最后得出结果的效果就会比较好。

这个我认为是比较投机取巧的方法，因为我们建模的目的不是为了比赛，我们需要的是能力，名次比较高的一些同学一部分同学就是有这种投机取巧的手段，这样实际套用到企业时，是没有办法得到比较好的训练数据。

去比赛其实是不是冠军，名次高不是很重要，他们是不是按照标准的步骤来，其实很难说。如果要用这种投机取巧的方式来做，一定要意识到实际到企业中，是不能有帮助的。这是题外话。

比如我们现在训练数据集有1000笔数据，有违约客户的比例是（yes，no）300：700。

第一种分割方式：

就是我们从这1000笔数据以不可取回的方式随机挑选800笔数据，剩下的200笔数据作为测试数据

第一种分割方式的缺点：

就是我们从这1000笔数据抽取出来的测试数据和训练数据违约客户的比例一般都不会满足3：7。与母体数据不合。

如果不计较这个缺点，也不失为一个好方法。

第二种分割方式：

这边是建议使用第二种分割方法，那么其他人的争议会少一点。

该方法就是分别从700笔数据和300笔数据中各自抽出百分之80作为训练数据集合。也就是把数据分为2层，一层为非违约客户，一层为违约客户，

700笔数据中我们挑选560笔作为训练数据集，300笔我们挑选出240笔作为训练数据集，剩下的140笔和60笔则加入测试数据集。

我们这样就会让数据抽出来的比例与母体相同，不管是测试集还是训练集都满足违约客户比例为3:7。

数据集：

训练集：就是为了训练模型M而创造出来的数据集

测试集，就是为了测试模型M而创造出来的数据集，

验证集：有些模型算法，为了降低模型过拟合的情况，会将测试集的一部分拿出来用来修正模型

一般训练集占用的数据数比较多

训练集占比百分之60

测试集占比百分之20

验证集占比百分之20

这里面的验证集不是每个模型都有的，很多模型比如朴素贝叶斯就没有验证集，这时就只有训练集和测试集。

但是决策树cart的算法就是需要验证集，这时就要把训练集的一部分当验证集。很多模块内部会自动做这个分离的的过程，所以就看到时候的应用来决定你把数据分为几类。

这种做法有一个缺点，就是每次取训练集和验证集，之后效能的产生都是不一样的。10次有10次效能不同，那么那个才是这个模型的小效能，这个就会有争议了

交叉验证

交叉验证就是会把数据分10笔数据，这里我们也会用可以按照分层抽样的方法来验证，保证分割结果与母体的分布相同。

交叉验证的原理就是我们每次都会抽取其中的9笔数据来测试其中一笔数据训练出的结果。这样的操作我们会重复10次。其中每一笔数据都会被测试一次。

然后我们就会根据这些数据结果去产生混淆矩阵，来评估模型，这个方法就比较没有争议的检验方式的检验方式

这和我们那1000笔资料直接去训练直接去测试是完全不一样的结果，后者的评估会很好。

这里的交叉验证分几个fold，fold数目越多，对模型的评估越好，但是比较耗时，交叉验证的极致就是（leave one out crossbvalidation）他是会把1000笔数据分为1000个交叉验证。效果自然最好但是结果最耗时，一般没人使用，10则交叉验证基本上就可以了。

建立模型的时候我们一般会建立一个基础模型（机械模型）baseline Model 作为比较的基准

机械模型建立如下：

分类问题：用众数建模，目标字段哪一类最多，就猜那一类，（根据实际情况而定）

回归问题：用均值或中位数建模

分类模型的评估

模型在一个决策点的评估：混淆矩阵、正确率（Accurracy）、查准率（Precision）、查全率（Recall）、F-指标（F-Measure）

首先是混淆矩阵（Confusion Matrix）：

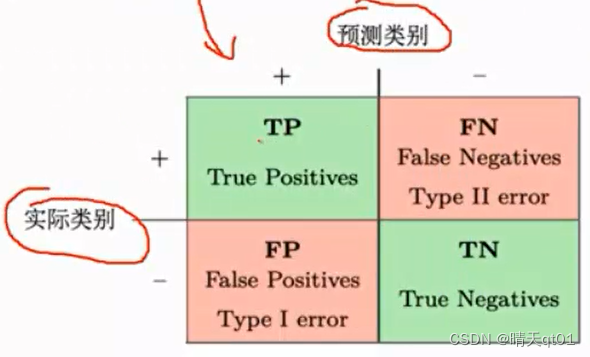
这里tp前面的T或者F代表是否预测正确，后面P（positives）和N（Negatives）代表预测的类型，TP代表预测p而且是正确的，

得到了这个混淆矩阵后，我们要如何计算我们的正确率，Accuracy

正确率accuracy那就是TP加上TN除以总笔数（tp+tn+fp+fn ）

查准率Precision代表的就是预测为P的实际对的比率。结果就是tp除以预测为p的笔数（tp+fp）

查全率recall代表的就是真实为P的，能够捕捉正确的P的个数。结果就是tp除以真实值为p的笔数（tp+tn）

F指标就是把查准率和查全率合并起来：因为如果光注重recall，不注重precision，会有缺点，光注重precision不注意recall也会有缺点。因为二者是可以根据内部的概率进行修改变化的。比如我希望precision的值高，那么我就把只要概率大于百分之99的值取为P，那么这时PRECISION的预测正确率就全对，但是可能就预测到一个是P。查全率就非常低。

如果我们预测全体人都是P，那么查全率就会非常高，查准率就会变为最低。

所以我们要同时考虑这两个指标。于是就产生了F1指标。

F1指标比较特别，比如我们现在precision值为0.1，recall的值为0.9，F1值会0.18，现在precision的值为0.5 recall的值为0.5，F1的值会是0.5。我们就会发现，如果二者不同的时候，F1值会偏小值小的。相同的时候，F1的值就是二者的值。

所以F1的指标就是为了让我们注重查全率和查准率二者。而不是注重其中一个。只有二者同时高，才能使它值高。

举个案例：

这个表的第一个字段为编号，第二个字段代表的是预测结果，第三个字段代表的是真实结果。

如果预测结果和真实预测结果不同就代表预测错误。

于是我们就可以画出我们的混淆矩阵，我们发现我们预测yes结果也为yes的数目为5，其他的以此类推。准确率就是5+2除以10，查准率就是 5/6差全率就是5/7 F1就是0.77

至于为什么我们要叫F指标为F1，是因为这个指标原本叫做F贝塔，因为我们把贝塔指标设为1，所以叫F1.

贝塔值是为了控制最后的F指标是要更偏向查全率还是查准率，当贝塔值设为大于1的时候，recall会重要与precision，如果设置为0.5就说明你比较重视precision查准率。

多分类模型的评估

多模型的评估

我们可以对每一类都进行建立混淆矩阵

这里我们每个类别我们都可以产生一个混淆矩阵，比如for a就可以产生一个混淆矩阵，这里面就可以发现，预测为A实际为A的为2笔，预测为A实际不为A的个数为0笔，预测不是A实际为A的也为2笔。因为右下角的数据没什么意义，所以我们就不去计算。其实可以计算出来，实际数值为5笔。查全率就是1.0查准率就是0.5，F1的数值就是0.667偏向小的。

同样的forB也是一样，我们也能得到他的混淆矩阵。并根据混淆矩阵求得查准率和查全率。

然后我们还有得到一个micro-F1，也就是把这些矩阵每个位置累加起来。这个3个表加起来的总混淆矩阵，我们也可以求得查全率和查准率，然后求出F1值。

而指标microF1就是将总混淆矩阵求出的数值除以3，把这个平均作为指标。这时是不看ABC3个类别的多少，而是单纯的考虑3个类别同等重要。进行求出的指标。

还有一个指标weightedF1，这个时候我们会把每个类别的数量作为评估的权重。然后得到最终的整体指标的评估。

今天我们讲了数据集的切割和分类模型在一个决策点的评估。

上次我们讲了分类模型在一个决策点上的评估，我们一般以模型预测出来的概率值，如果概率大于0.5我们就预测为第一类，否则就预测为第二类，

如果是分多类模型，比如分3类问题，3类问题的概率之和就会等于1，然后其中概率最大的那类就会变为我们的预测模型。

当然我们也可以选择，大于等于0.6才预测为1，否则就预测为0，大于0.7也可以，我们可以选择各种概率来进行分类，那么就变成了多个决策点问题，我们也需要对模型进行一个整体的评估，在各种门槛值之下，进行一个决策点的评估，这时模型的好坏就和门槛值有关系，可能门槛值由0.6变为0.7就会导致前者的模型比后者不好。

整体性的评估的话，它就只会有一个值，它会考虑各个门槛值。所以今天就考虑分类模型的整体评估。

分类模型的整体评估：

当我们做模型的整体性评估的话，我们就不需要你的预测结果，我们需要的是预测结果的概率值。

第一笔是预测它的概率为0.9，第二笔预测概率为0.8，这里的概率是已经排序过了，概率越大，说明模型越有把握它是1。

排序之后，我们就会发现1大部分分布在上面，0大部分分布在下面，如果我们能清楚的做出这种0和1的分布，说明这个模型是还不错的模型。结果用传统的0.5为门槛值来做分类，这样就可以产生旁边的混淆矩阵，这里左上角代表有7个预测结果为0真实结果也为0，以此类推。然后我们就可以根据混淆矩阵来计算查全率率。查准率，F值。

这里面我们可能会遇见比较特别的sensitivity和true positive rate，其实代表的也是recall也就是查准率。

Specificity代表的就是查准率相反的概念，也就是预测为0且预测正确的比率。

1-specificity就是false positive rate，这边有一些名词是会在文献里出现，可能来对照一下。

如果我们把门槛值调整为0.375

也就是说我们把预测1的比例变多了有13笔。其中有3笔是预测错误，预测0的剩下7笔，预测错误的为1.

我们就可以吧正确率这时正确率就是百分之20，也就是6+10除以总数20

F值就是0.83，放宽之后虽然查全率变低了，但是查准率高了很多，所以F值增加了。

最终评估标准如果是F1，那么就是一个最优化的问题，要如何修改我们的门槛值，让我们的F1值最高。如果掌握单一决策点也是一个技术。模型其实没有变，但是门槛值的变化让效果更好了。

有些比赛要对模型的整体进行评估。它是不会由于模型的门槛值变化而改变模型的评估指标的值，它会考虑所有门槛值。

下面介绍第一个总体评估指标KS图

KS图（KS Chart）

KS值是一个介于0-100的值，这个值越大越好，怎么计算呢：

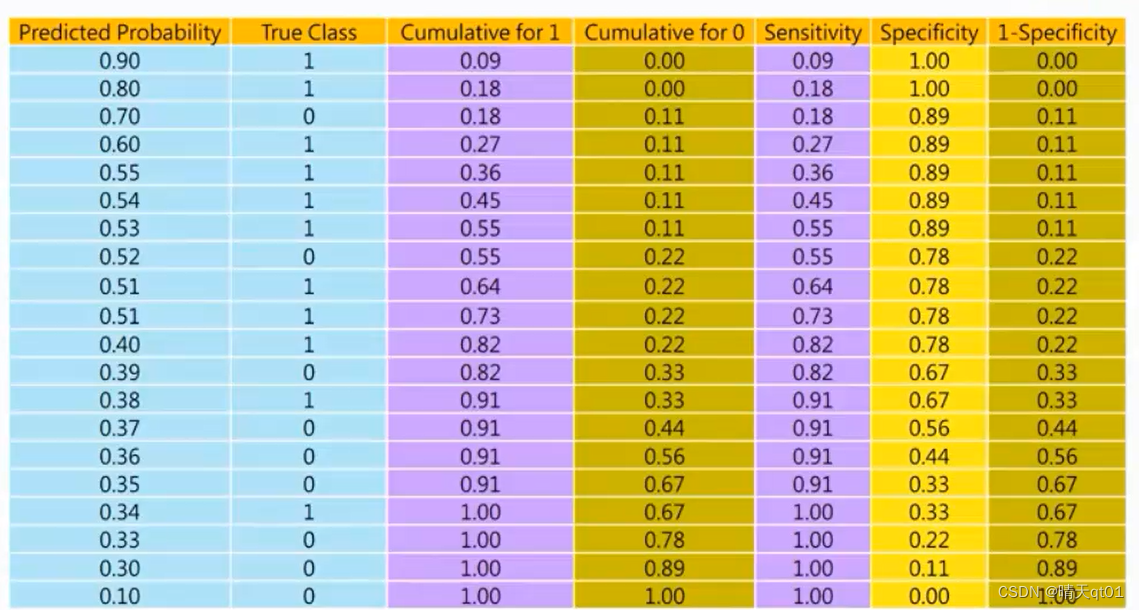
就是我们还是把概率值从大到小排序，第二个字段是真实值。第三个字段我们去对真实值，累积1的频率，第4个字段我们去累计真实值0的频率。

因为我们好的分类模型，会让1集中在上方，0集中在下方，所以累积1的频率会比较快，累积0的百分比会很慢，但是到后面累积0的百分比会越来越快，累积0的百分之百就会越来越慢。

KS值是我们就采用字段3累积1的百分比减去字段4累积0的百分比，产生值参与100，放入字段5，然后我们就会得到各种ks值，我们去寻找ks值的最大值，因为此时就是它们被分的最开的地方。累积1和累积0的频率差距最大的地方，这个值就是模型的KS值作为整体评估模型。作为模型好不好的评分，

我们可以查看KS的可视化散点图：

我们可以发现刚开始的1的点累计的速度非常快，0累计的速度很慢，后面0累计的速度就非常快了，中间差异最大的就是ks值为60。所以ks值就是60

那么ks值为60究竟是高还是低呢，我们一会有一个表格，可以用来查看该模型的好坏。

如果ks值都是100代表一开始都在累计1,0完全没有累计，也就是所有的1都在前面，0都在后面，这时的ks值才能是100,。

最差的时候就是0分。。

风险评估的时候会有一个参考值。

比较特别的是，大于75的时候可能说明模型有问题。可能是我们把目标字段当做输入字段，把果做因，所以要检查一下，可能哪里有问题。

之前有一些人做客户流失的模型，定义就是一年之内和我们没有外来，其中一个字段是客户有多久没和我们往来了。那客户多久没和我们往来的数值越大就说明客户流失的概率越大，那么这么建立的ks值就非常高，75左右，但是这个肯定是有问题，我们都把客户12个月未和我们往来就是流失，你字段里又用客户多久与我们往来作为判断依据，那这个就是用果做因，这两个很接近。

如果ks值非常高，有可能就是模型出了一些问题，模型值为51~60其实就很好了，企业的模型其实没那么好做。

另外我们可以把利润算出来，也就是判断成功，我们会赚多少钱，预测失败会亏损多少钱。这种情况要得到利润最高的模型，我们可以吧利润profit累积作为模型评估指标。

正确时就会得到100的利润，预测错误时就是-200的利润

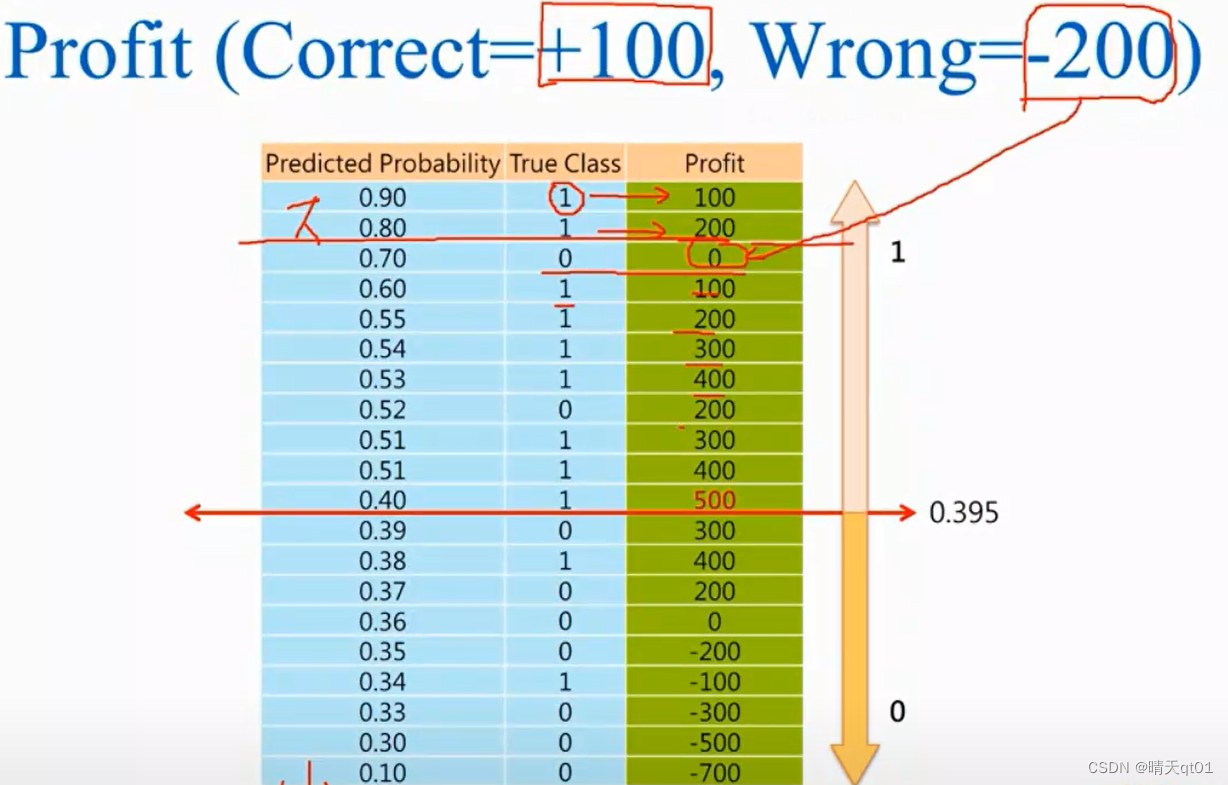
同样，我们把预测为1的概率从大到小排序，进行累积理论的求职这个时候，我们看看我们的利润什么时候是最大值，预测为1的概率门槛值为0.395，就可以得到最高的利润500，这个也是模型的评估指标，我们决定一个最大的理论，决定为我们的整体指标。

它和ks值的差别就是角度不同，这个是从利润进行，而ks值是根据累计1和累积0的差异最大化的角度作为指标。

主要是看公司要以哪个为角度

ROC图（ROC chart）

这也是一个比较有名的方法，这个将它曲线围成的面积当做整体模型的评估指标，auc

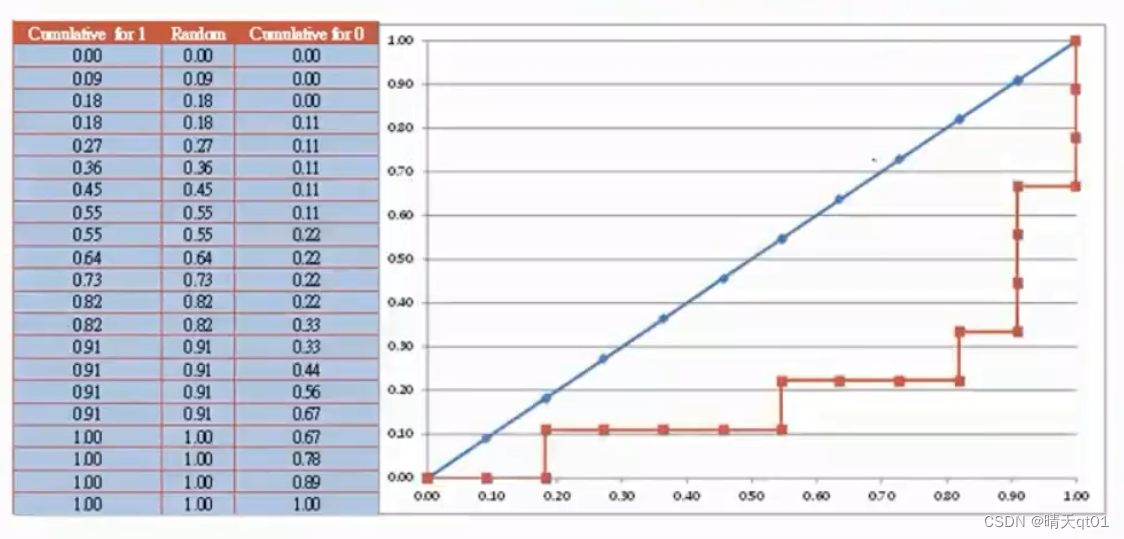
它也是将模型预测为1的概率从大到小进行排序。需要产生的字段分别是累积1的百分比，累积0的百分比，，我们直接根据这两个字段的值作为坐标，去画点，画出来的roc

我们将这图的3，4的两个字段画出的坐标图如下。

累积1的百分比当做x，累积0的百分比当做y，对应画出来的直线是图中蓝色的图线，这条线由于累积1的值会一直往上冲到后面累积0的百分比才会开始懂，就会导致出现图中的情况。Roc coffee围出来的的面积就是下图

这个面积最大是百分之百（1*1）越大越好。45度的线代表的就是我们随机乱猜的预测结果。，其中45角的这条线围成的面积为0.5模型通常的roc曲线大于0.5如果低于这条曲线，那么代表比随机乱猜还低的正确率，这样是不太可能

AUC值在0.5-1之间

教科书中课本喜欢叫y轴（事实就是累积1的百分比）sensitivity，x轴就是累积0的百分比。都要了解，不然可能人家写的你看不懂，

模型的评估会按照这个模型围成的面积来

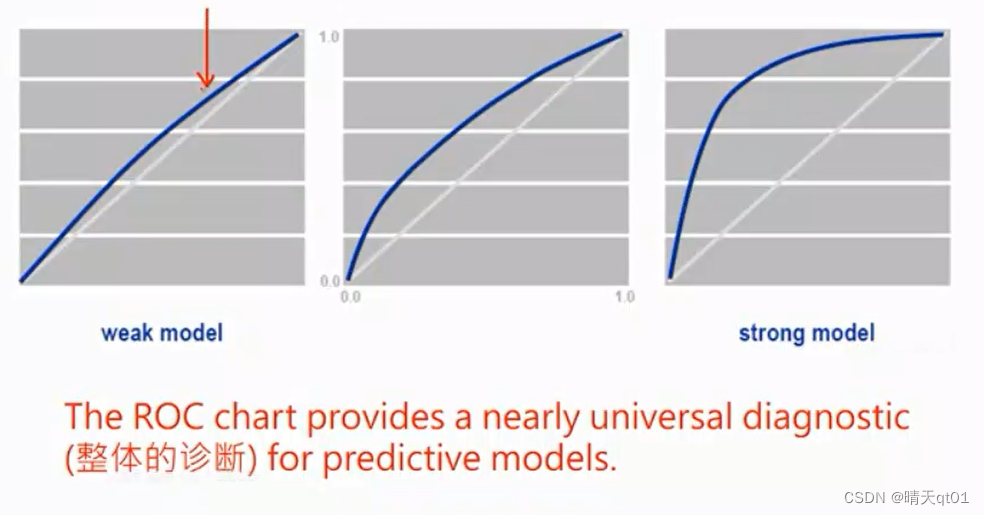
相当于每个门槛值都一起考虑了，我们这个面积一般叫做AUC或者roc index，这里的auc值通常会大于0.5小于1.0这个值如果

如果AUC只是比大一点那么这个模型就是比较弱的模型，如果大于0.7那么该模型就是比较强的模型。

另外这里出一道题给大家，如果阈值很大，然后逐渐减小阈值，那么各位认为ROC曲线应该如何移动。

应该是从00-11移动

AUC也是具有一个极限，一会和gini指标一起说了

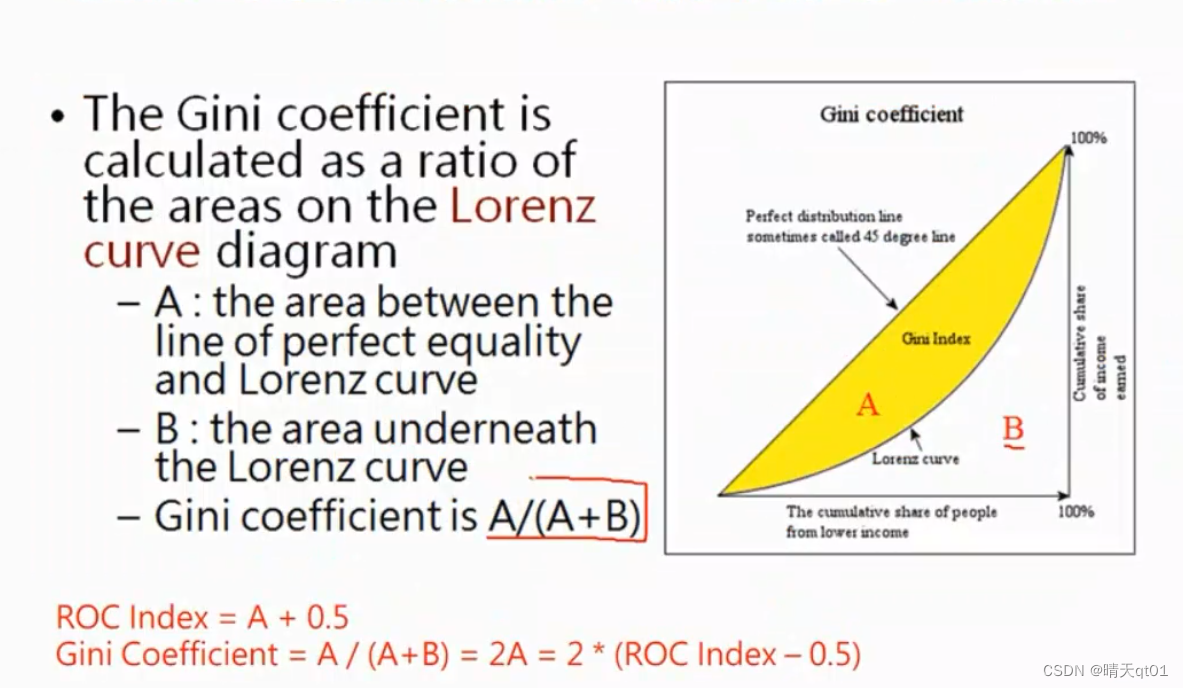
GINI图（GINI Chart）

Gini图的指标其实和roc图非常相似，roc图是将累计0作为x值，累计1作为y值，而gini图则是将二者颠倒，人累计0作为y值累计1作为x值，所以它画出来的图就会是下面这样，

刚开始都是累计1很快，然后累计0很快，其实根据y=x对称过来就是Roc图，gini index的值就是就是A+A/B或者A/（A+B），比较好的情况就是B很小，A很大的情况。这代表B的面积越小越好，

这个就是gini index又因为 A+B就是等于0.5，所以公式的值其实就是2A，，AUC的值又是A+0.8所以A会等于什么，

A=ROC idex -0.5=

所以giniindex=2roc index-1

Gini值也是有固定指标：

这里一个评分参考不同的应用其实不一定是这样，这时一般做信用卡评分模型的时候用这个指标

比如阿里巴巴没有得到银行的授权数据做的一个顾客评分表，数值就是很低，只有0~0.4，但也不能说它辨识能力就极差，所以我们要知道这个图只是一个参考而已。

回应图，（Response Chart）

其实最重要的chart和指标我们都已经介绍完毕，response chart，其实就是在计算模型它的precision，这里是在计算营销的回应率，一样是吧概率从大到小排列，然后模型的指标是按照预测一的精度来计算，刚开始如果预测1正确就是百分比，第二次也是预测1还是百分百，第3个因为预测为1，但是预测结果是0所以精确度变为0.67，回应率会随着概率的减少而越变越小，因为一般1都集中在前面，因为这些就是模型比较有把握的人，然后你去做营销，回应率比较高的地方肯定在前面。

如何画出这个图呢，我们会把横坐标设定为以人数，或者营销一个人的频率，比如这里有20个数据，那么频率就会设定为0.05

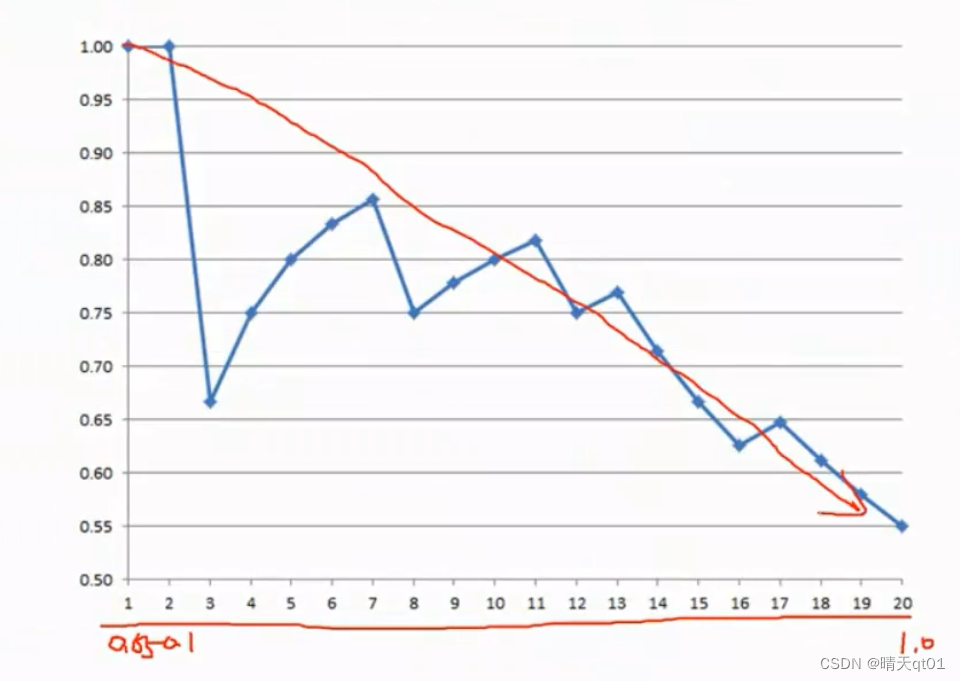
按理所回应率是随着人数的增加逐渐减少的，但是这里有高有低，这是因为人数比较少，所以会出现这种情况，营销的人数越多，回应率也就会越来越差。

增益图（Gain Chart）

另外还有一个Gain Chart的表格，它的y轴就是累积1的百分比，当累积1的时候就会增加比率，前面累积1比较快，后面累积0比较快，营销的人越多，之前回应图的precision会越来越低，该图的recall会越来越多。

如果把二者的图像画在一起就会出现下图的情况，相交的点很可能就是F1指标最好的情况。因为F1追求的就是recall和precision都很高的情况。

也可以再画一个F1值的预测：

它的值大概率是介于二者之间，也可以找到最佳的F1值。

提升图（Lift Chart）

提升图也是先把概率由大到小排列，1有11个，字段3是如果随机乱猜的情况，累积1的百分比提升情况

也就是45度角那条线，而第4个字段对应的是实际累积1概率的值，最后一个字段lift就是提升程度，是累积1的值除以随机乱猜的值得到的数值，也就是我的模型在每个点比模型要好多少，第一个点，我的模型要比随机乱猜好1.8倍，第二个点，我的模型要比随机乱猜好1.8倍，以此类推。就是在算比随机乱猜好的倍数，

画图就是将以人数123为x轴，好的倍数为y轴画到坐标轴上，

也就是营销的人越来越多的时候，提升度也会越来越低，因为到后面没有把握的时候就会降低。整体很类似precision，营销的人越多的时候，lift的值，模型比随机乱猜好的倍数通常会越来越少。最极端的情况就是，我认为所有人都合格，都不违约，那么有没有模型都一样。

回归模型的评估：

平均绝对误差（Mean Absolute Error）

真实值减去预测值，误差有正有负，N笔资料的预测，就是将误差取绝对值进行累加除以n笔数据。

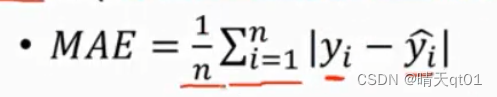
这时平均绝对误差

平均平方误差（Mean Squared Error）

真实值减去预测值，这时将误差值取平方，进行累加然后除以N笔数据。

但是有些人认为你既然加平方了，那么就应该加个根号才能让你这个值显的不那么大，于是就出现了均方根误差

均方根误差（Root Mean Squared Error）

就是把MSE算出来的值开一个根号。

上面的MSE MAE RMSE都是计算机喜欢使用的评估指标，但是MAE和MSE的差别在哪里，这边我们举一个例子，在逻辑上有一定的差别，这里我们有2个模型A和B，两个模型有相同的MAE都是10，那例如说我们的第一个模型，A有两笔数据，第一笔数据的误差为0，第二步误差为10。B这个模型第一笔资料的误差是5，第二步资料的误差也是5，

MAE把A模型误差相加就是10，值为5，B模型也是5，认为两个模型一样好。

我们通常会比较喜欢B这个模型，因为A这个模型会出现一种情况，有时候预测非常准，有时候又误差很大，模型很不稳定，B这种模型虽然有误差，但是预测一直比较稳定，不会忽大忽小，我们的MAE不能评估这个现象，我们如果用平方误差，第一个模型平方误差为50 第二个模型是25，如果以平方误差的角度来看，那么B这个模型比较好，所以平方误差其实是有在惩罚误差特别大，不稳定的模型，这个就是MAE和MSE的差别，所以MAE会一视同仁，MSE会把误差特别大的放的更大，中间是有逻辑上的不同。

R2以及Adjusted R2

统计上不喜欢这种模型，上面的模型都是计算机的人建立出来的，得到的值25,50，这个值究竟是好还是不好，MAE值应该大于多少以上才算不会，MAE值应该小于多少才算好。你得定个指标出来。

我们就会说因为每个预测出来的数值都不一样，所以你不可能定一个通用值，那统计的学者就不会用这些指标，而是用R^2和调整R^2，它有一个好处就是，R^2和调整R2是一定介于0-1之间的，无论是预测年薪还是库存量，算出来的结果一定在0-1之间，越靠近1越好，靠近0越不好，这样我们就可以确定一个指标，0.8,0.6之类的值，只要大于该值，就说明该模型很好。小于0.8就是不好。或者分级，0.2,0.4,0.6，0.8来定这个模型的等级，好，一丢丢好，一般好，非常好。

这里面有几个指标