Vision Transformer图像分类
Vision Transformer(ViT)简介
近些年,随着基于自注意(Self-Attention)结构的模型的发展,特别是Transformer模型的提出,极大地促进了自然语言处理模型的发展。由于Transformers的计算效率和可扩展性,它已经能够训练具有超过100B参数的空前规模的模型。
ViT则是自然语言处理和计算机视觉两个领域的融合结晶。在不依赖卷积操作的情况下,依然可以在图像分类任务上达到很好的效果。
模型结构
ViT模型的主体结构是基于Transformer模型的Encoder部分(部分结构顺序有调整,如:Normalization的位置与标准Transformer不同),其结构图[1]如下:
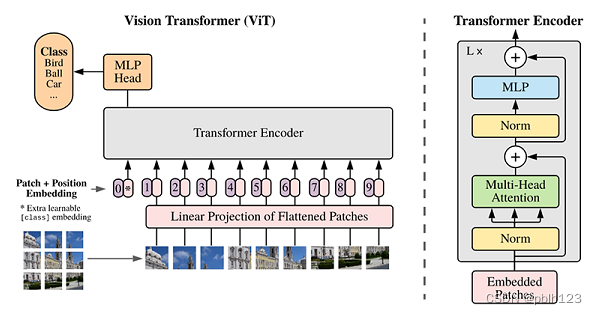
模型特点
ViT模型主要应用于图像分类领域。因此,其模型结构相较于传统的Transformer有以下几个特点:
- 数据集的原图像被划分为多个patch(图像块)后,将二维patch(不考虑channel)转换为一维向量,再加上类别向量与位置向量作为模型输入。
- 模型主体的Block结构是基于Transformer的Encoder结构,但是调整了Normalization的位置,其中,最主要的结构依然是Multi-head Attention结构。
- 模型在Blocks堆叠后接全连接层,接受类别向量的输出作为输入并用于分类。通常情况下,我们将最后的全连接层称为Head,Transformer Encoder部分为backbone。
下面将通过代码实例来详细解释基于ViT实现ImageNet分类任务。
注意,本教程在CPU上运行时间过长,不建议使用CPU运行。
环境准备与数据读取¶
开始实验之前,请确保本地已经安装了Python环境并安装了MindSpore。
首先我们需要下载本案例的数据集,可通过http://image-net.org下载完整的ImageNet数据集,本案例应用的数据集是从ImageNet中筛选出来的子集。
运行第一段代码时会自动下载并解压,请确保你的数据集路径如以下结构。
.dataset/
├── ILSVRC2012_devkit_t12.tar.gz
├── train/
├── infer/
└── val/实践环境安装
Python环境为 3.9.19
pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore==2.2.14
# or
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple mindspore==2.2.14
数据准备
from download import download
dataset_url = "https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/datasets/vit_imagenet_dataset.zip"
path = "./"
path = download(dataset_url, path, kind="zip", replace=True)
import os
import mindspore as ms
from mindspore.dataset import ImageFolderDataset
import mindspore.dataset.vision as transforms
data_path = './dataset/'
mean = [0.485 * 255, 0.456 * 255, 0.406 * 255]
std = [0.229 * 255, 0.224 * 255, 0.225 * 255]
dataset_train = ImageFolderDataset(os.path.join(data_path, "train"), shuffle=True)
trans_train = [
transforms.RandomCropDecodeResize(size=224,
scale=(0.08, 1.0),
ratio=(0.75, 1.333)),
transforms.RandomHorizontalFlip(prob=0.5),
transforms.Normalize(mean=mean, std=std),
transforms.HWC2CHW()
]
dataset_train = dataset_train.map(operations=trans_train, input_columns=["image"])
dataset_train = dataset_train.batch(batch_size=16, drop_remainder=True)模型解析
下面将通过代码来细致剖析ViT模型的内部结构。
Transformer基本原理
Transformer模型源于2017年的一篇文章[2]。在这篇文章中提出的基于Attention机制的编码器-解码器型结构在自然语言处理领域获得了巨大的成功。模型结构如下图所示:
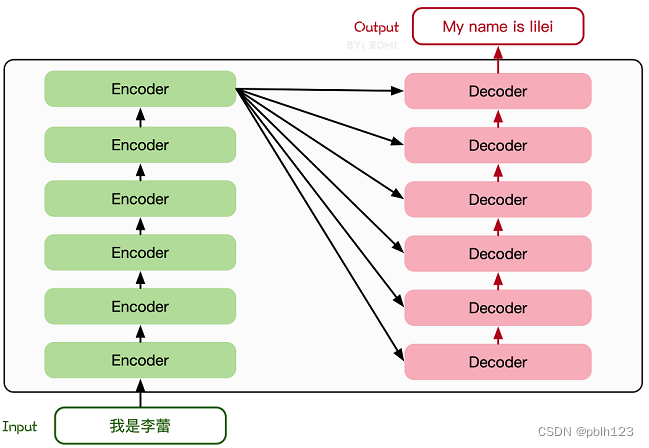
其主要结构为多个Encoder和Decoder模块所组成,其中Encoder和Decoder的详细结构如下图[2]所示:
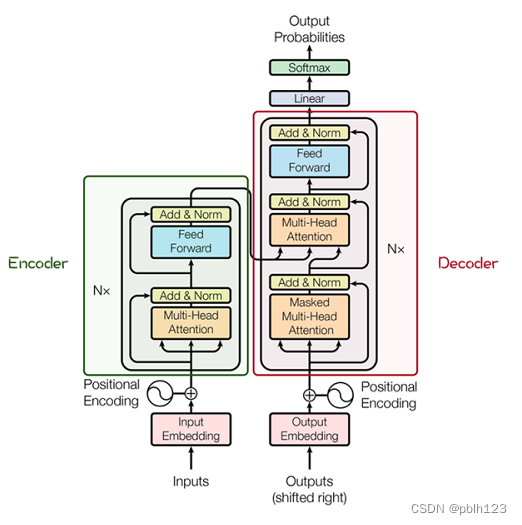
Encoder与Decoder由许多结构组成,如:多头注意力(Multi-Head Attention)层,Feed Forward层,Normaliztion层,甚至残差连接(Residual Connection,图中的“Add”)。不过,其中最重要的结构是多头注意力(Multi-Head Attention)结构,该结构基于自注意力(Self-Attention)机制,是多个Self-Attention的并行组成。
所以,理解了Self-Attention就抓住了Transformer的核心。
Attention模块
以下是Self-Attention的解释,其核心内容是为输入向量的每个单词学习一个权重。通过给定一个任务相关的查询向量Query向量,计算Query和各个Key的相似性或者相关性得到注意力分布,即得到每个Key对应Value的权重系数,然后对Value进行加权求和得到最终的Attention数值。
在Self-Attention中:
1. 最初的输入向量首先会经过Embedding层映射成Q(Query),K(Key),V(Value)三个向量,由于是并行操作,所以代码中是映射成为dim x 3的向量然后进行分割,换言之,如果你的输入向量为一个向量序列(𝑥1,𝑥2,𝑥3),其中的𝑥1,𝑥2,𝑥3都是一维向量,那么每一个一维向量都会经过Embedding层映射出Q,K,V三个向量,只是Embedding矩阵不同,矩阵参数也是通过学习得到的。这里大家可以认为,Q,K,V三个矩阵是发现向量之间关联信息的一种手段,需要经过学习得到,至于为什么是Q,K,V三个,主要是因为需要两个向量点乘以获得权重,又需要另一个向量来承载权重向加的结果,所以,最少需要3个矩阵。
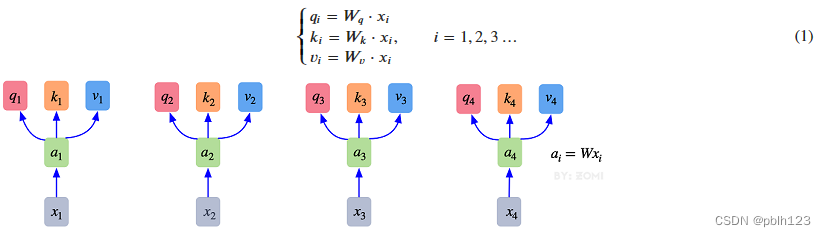
2. 自注意力机制的自注意主要体现在它的Q,K,V都来源于其自身,也就是该过程是在提取输入的不同顺序的向量的联系与特征,最终通过不同顺序向量之间的联系紧密性(Q与K乘积经过Softmax的结果)来表现出来。Q,K,V得到后就需要获取向量间权重,需要对Q和K进行点乘并除以维度的平方根,对所有向量的结果进行Softmax处理,通过公式(2)的操作,我们获得了向量之间的关系权重。
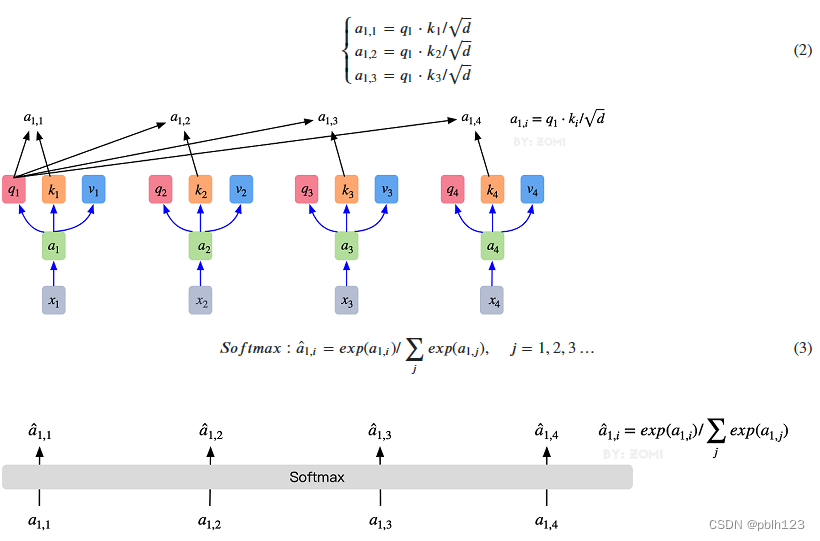
3. 其最终输出则是通过V这个映射后的向量与Q,K经过Softmax结果进行weight sum获得,这个过程可以理解为在全局上进行自注意表示。每一组Q,K,V最后都有一个V输出,这是Self-Attention得到的最终结果,是当前向量在结合了它与其他向量关联权重后得到的结果。
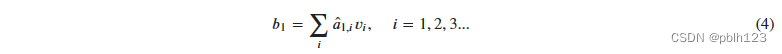
Self-Attention的全部过程

![[SIEMENS/S7-300] 接线图分析](https://img-blog.csdnimg.cn/img_convert/f882d5b8e9eaf764a56e7fb02f3a7a96.jpeg)