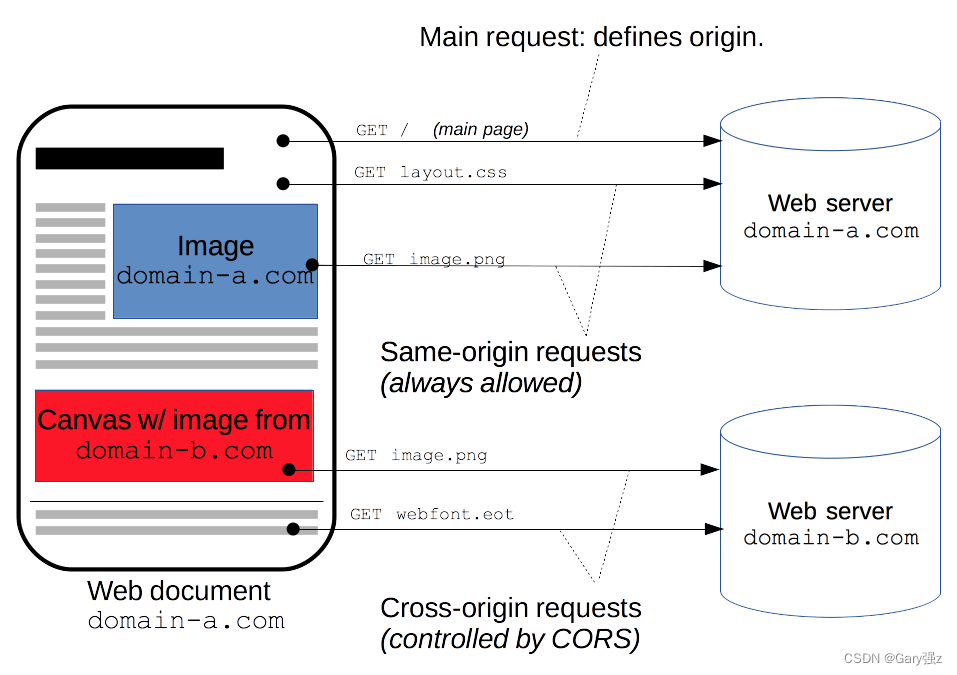
并联机构运动学
对于并联机构的位置正解、位置逆解和对应于位置解的速度、加速度进行分析是并联机构运动学分析主要内容。与串联机构不同,一般并联机构的位置逆解相对要简单,而位置正解则求解比较复杂些。并联机构的位置正解的求解过程中,大多需要对多元非线性方程组进行求解。
目前对于求解位置逆解的方法可分为两类:
- 闭环矢量解析法:即根据并联机器人的运动学闭环特性,通过矢量运算即可求得;
- 螺旋理论法:利用对并联机构各关节进行旋量表示,再利用螺旋理论即可求得运动学模型.
求解位置正解的方法主要有:1、数值法;2、解析法
详细建模过程
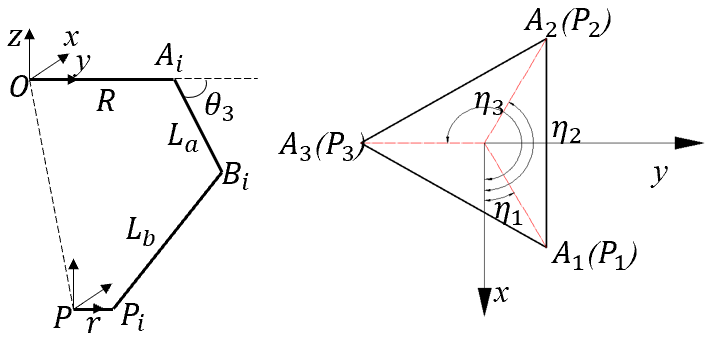
- 建立如右图所示的坐标系,其结构参数如图所示。
- 根据建立的坐标系和各参数的假设,可以得出以下点在基坐标下的坐标:
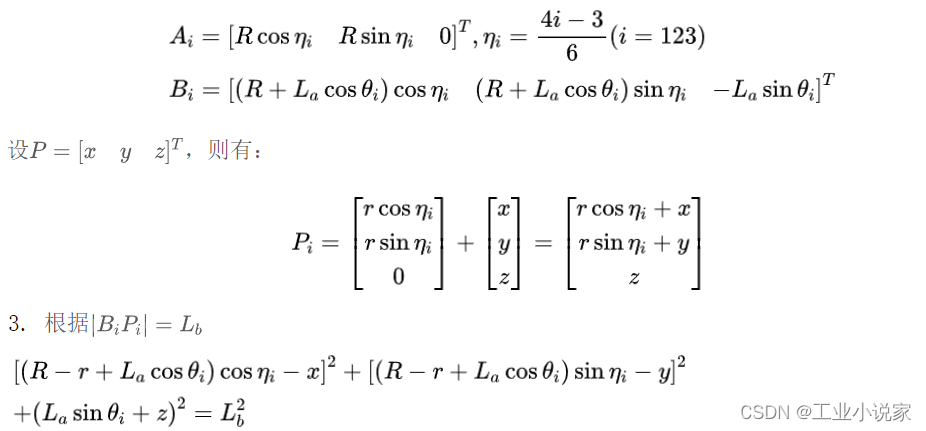
运用三角函数万能公式:
sin θ i = 2 t 1 + t 2 cos θ i = 1 − t 2 1 + t 2 \sin {\theta _i} = {{2t} \over {1 + {t^2}}}\cos {\theta _i} = {{1 - {t^2}} \over {1 + {t^2}}} sinθi=1+t22tcosθi=1+t21−t2
对上式进行整理并化简为:
M i t i 2 + N i t i + Q i = 0 , i = 123 {M_i}t_i^2 + {N_i}{t_i} + {Q_i} = 0,i = 123 Miti2+Niti+Qi=0,i=123
根据求解公式,求解得:
t i = − N i ± N i 2 − 4 M i Q i 2 M i {t_i} = {{ - {N_i} \pm \sqrt {N_i^2 - 4{M_i}{Q_i}} } \over {2{M_i}}} ti=2Mi−Ni±Ni2−4MiQi
分析该机器人的空间位置结构方程最终取得一个解为:
t i = − N i + N i 2 − 4 M i Q i 2 M i {t_i} = {{ - {N_i} + \sqrt {N_i^2 - 4{M_i}{Q_i}} } \over {2{M_i}}} ti=2Mi−Ni+Ni2−4MiQi
该机器人的驱动角为: θ i = 2 arctan ( t i ) {\theta _i} = 2\arctan ({t_i}) θi=2arctan(ti)
至此,Delta机器人运动学逆解推导完成,下一篇推文我们将详细讲解如何在MATLAB中进行该机器人的运动学仿真。
往期推荐