二叉树的销毁

分为三个部分的销毁：根节点，左子树和右子树

void TreeDestory(BTNode* root)
{
   if(root==NULL)
     return;
   TreeDestory(root->left);
   TreeDestory(root->right);
   free(root);
   root=NULL;
}

层序遍历（上一层带下一层）

typedef struct BinaryTreeNode* QDtaType;
void TreeLevelOrder(BTNode* root)
{
  Queue q;
  QueueInit(&q);
  if(root)
    QueuePush(&q,root);
  while(!QueuEmpty(&q))
  {
     BTNode* front=QueueFront(&q);
     QueuePop(&q);
     BTNode* front = QueueFront(&q);
     printf("%d ",front->data);
         if(front->left)
            QueuePush(&q,front->left); 
         if(front->right)
            QueuePush(&q,front->right);
    
  }
  QueueDestory(&q);
}

队列里面的指针指向树的节点，把节点释放掉，不会影响到树的节点。

判断二叉树是否为完全二叉树：

1、层序遍历走，空也进队列

2、遇到第一个空节点时，开始判断，后面全空就是完全二叉树，后面有非空就不是完全二叉树。 

bool TreeComplete(BTNode* root)
{
   Queue q;
   InitQueue(&q);
   if(root)
      QueuePush(&q,root);
   while(!QueueEmpty(&q))
   {
      BTNode*front=QueueFront(&q);
      QueuePop(&q);
     //遇到第一个空，就可以开始判断，如果队列中还有非空，就不是完全二叉树
      if(front==NULL)
   {
       break;
   }
   QueuePush(&q,front->left);
   QueuePush(&q,front->right);
  }
  

不可能出现，遇到空时，后面还有非空没进队列。

后面非空，一定是前面非空的孩子。

当层序出到空的时候，前面非空都出完了，那他的孩子一定进队列了。

那么这时候就不需要担心。

二叉树的性质

1.规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个节点，

2.若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h-1，

3.对任何一棵二叉树，如果度为0，其叶子结点的个数为n0，度为2的分支结点个数为n2，则有n0=n2+1，（增加一个度为1，减少一个度为0）

4.若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log2（n+1）

5.对于具有n个节点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的节点有：

题目：具有2n个节点的完全二叉树中，叶子结点的个数是多少个

n0+n1+n2=2n

n0=n2+1 得 2n0+n1-1=2n，

完全二叉树中n1等于1或0

当n1等于0，左边不可能为偶数；当n1等于1，左边才可能为偶数，所以推导出来n0=n。

一棵完全二叉树的节点数为531，那么这棵树的高度为多少？

由前面我们可以知道，一棵完全二叉树的节点数是2^h-1个节点。那么此时，我们可以看最少有多少个节点，也就是h-1层。也就是2^(h-1)-1。（本题算范围）

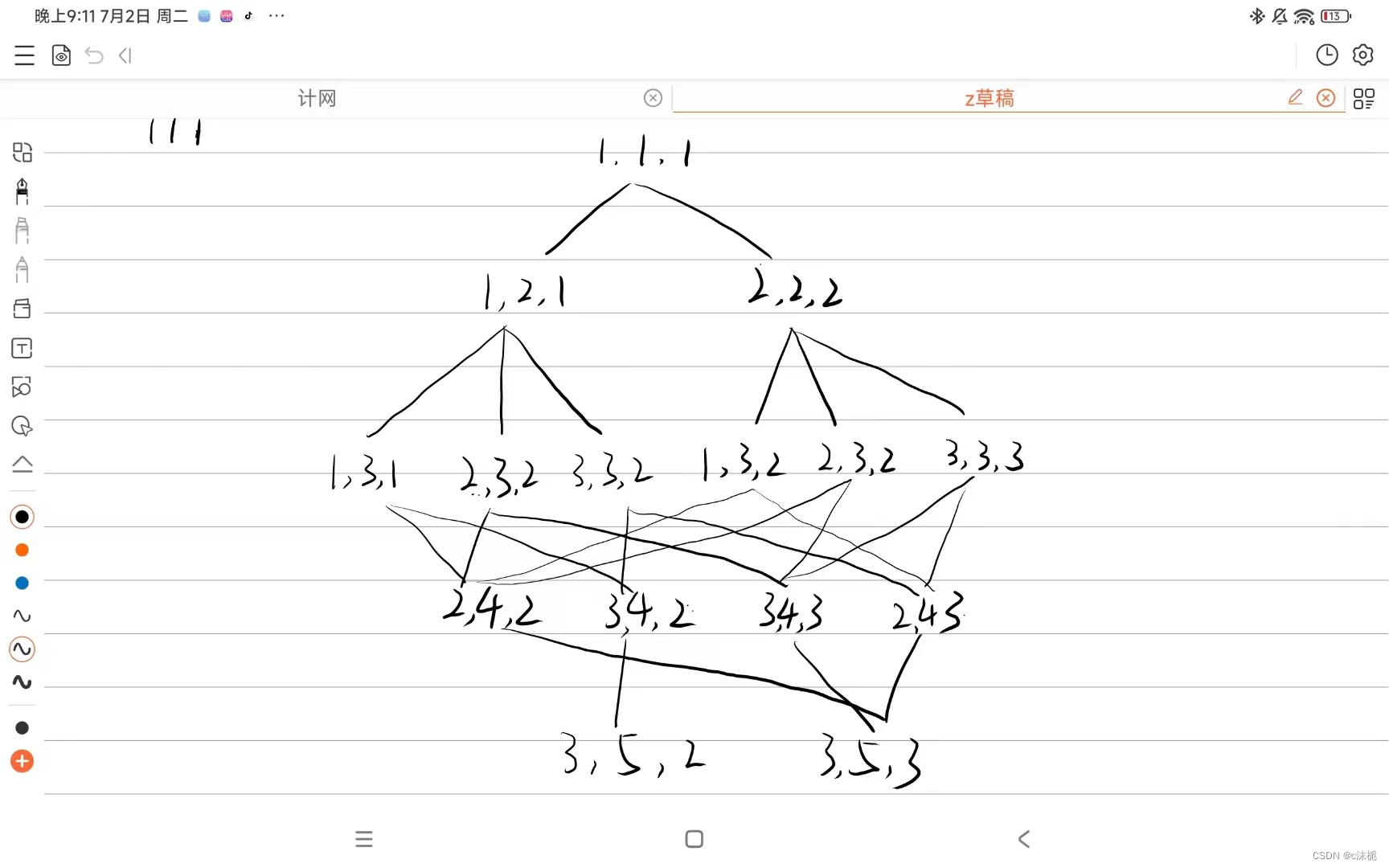
还原二叉树

前序确定根，中序分割左右子树。由前序可以知道，1一定是跟，那么就可以分为这两片：

进一步确定

然后又可以确定4为右子树的根：