目录

一、动态规划算法概念

 题一

1、算法解析

1）确定状态：

​2）状态转移方程：

​3）初始化：

4）填表顺序：

5）返回值：

2、代码

题二

1、算法解析

1、确定状态

2、状态转移方程

3、初始化

4、填表顺序

5、返回值

2、代码

3、空间优化版本

 题三

1、算法解析

1、确定状态：

2、状态转移方程：

3、初始化：

4、填表顺序：

5、返回值：

2、代码

  题四

1、算法解析

1、确定状态：

2、状态转移方程：

3、初始化：

4、填表顺序：

5、返回值：

2、代码

一、动态规划算法概念

首先，什么是动态规划？
很简单，就是动态的规划。呃.....
概念名不要紧，重要的是理解其算法思想，并且能够灵活的运用其思想和方法来处理和解决现实生活中的问题，即改造世界。
动态规划的思想，具有很强的抽象性，例如什么重复子结构、最优子结构等等，你一听就晕了，这什么玩意？
一般来说，学校的课程教学，很学院派。通常是直接灌输式的给你一个世界观和方法论，然后直接让你去屠龙。
这个是一个超越经验的东西，直接给你了。但是，我们并不能理解这个结论，因为太抽象。
算法是一个由很多具体问题，经过长期总结归纳而形成的一个经验过程。算法思想算法思想，为什么不是算法公式呢？这是因为无法统一，只能是思想。
需要结合很多具体的实际问题来进行，来体会，来联系，来加深理解。
因此，在我的算法栏目中，是不会直接给你丢一堆归纳性理论的，而是，先告诉你是什么
然后再告诉你要怎么做。多做题，在这个过程中，你需要自己领悟体会。
体会什么？通过许多例题的解决过程，慢慢形成经验的直觉，再去变通，举一反三，而后融会贯通。
同志，共勉之。

下面我们直接上手，我会给你一个固定的，过程性解决问题的套路模板。
然后你根据这个模板，去套题目，找出相关的变量和关键因素。
再根据此去写代码。
动态规划，一般分为5个步骤：

1、确定状态：
刚开始一般会先画一个dp表，再去填表，某一个位置的值就是解

这一步要做的就是：明确dp数组里面的值所表示的含义
就是 dp[i] 这个值，是什么意思？
那么，怎么定义状表示呢？
这个要根据题目要求具体分析
一般来说，一维数组的状态表示，有两种：
以i为结尾，如何如何；或者以i为起点，如何如何。

2、状态转移方程：
状态转移方程就是：dp[i] 等于什么 ？
一般来说，状态转移方程，就是根据 dp[ i ] 之前或者 dp[ i ] 之后，来推导出 dp[ i ] 的值
只要你能根据之前或或者之后的值来推导出 dp[ i ] 的值
那么，状态转移方程就出来了
但是，怎么推？
这个就要就题目而言
但是，大体的思路是这样的：根据最近的状态来划分问题
一般来说，dp[i] 的值，要么是前面的 dp[i-1] 或者后面的 dp[i+1]

3、初始化：
初始化就是保证，在我们进行填表的时候不越界
例如说，我要求 dp[0] / dp[1] 的值，需要前面的位置，但是此时明显已经越界
因此，这两个位置需要单独处理

4、填表顺序：
什么是填表顺序？
很好理解，例如说
i位置值得求解，需要前面两个位置的值已经存在才能求解
因此，也就是说在算i位置时，i-1 和 i-2 位置已经填了，已经有值了
所以，我们的填表顺序应该是从前往后，因为后面的值的求解需要前面的值
反之，就是从后往前。

5、返回值：
就是看你要dp数组的哪个位置的值，
题目要去要什么值，你就根据题目给他return就好。
这个很好理解吧？

6、代码书写
动态规划的代码书写过程是比较固定的，一般来说就分成四个步骤：
1）创建dp表
2）初始化
3）填表
4）确定返回值

7、空间优化：
空间优化就是不需要那么多空间，就可以实现目的。
怎么实现呢？
滚动数组：从左向右赋值还是从右向左赋值
这个在后面的题目中会提到。

ok，讲到这里，你懂了吗？
没听懂？那就对了。
下面跟着我来，很简单，放轻松。
我会带你把这些套路用上，去分析解决问题，跟着我的思路就好。
前面比较简单的题目我会给的非常细致，后面逐渐粗略。

 题一

746. 使用最小花费爬楼梯 - 力扣（LeetCode）

1、算法解析

1）确定状态：

确定状态是在干什么？
就是确定状态dp数组中的值代表什么含义。根据分析，我们发现：

状态表的dp[i]值是到达该位置的最小花费

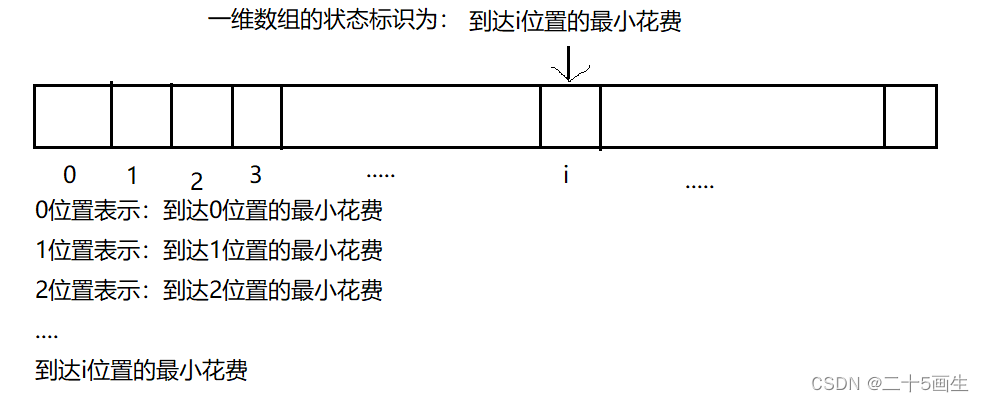
2）状态转移方程：

一般来说，状态转移方程，就是根据i位置之前或者i位置之后，来推导出i的值
只要你能根据之前或或者之后的值来推导出i的值
那么，状态转移方程就出来了
但是，怎么推？
这个就要就题目而言
但是，大体的思路是这样的：根据最近的状态来划分问题

在这个题目中，我们第 i 位置的值，需要前面两个位置的值来确定，其分析过程如下：

3）初始化：

初始化就是保证，在我们进行填表的时候不越界
例如说，我要求dp[0]/dp[1]位置的值，需要前面的位置，但是此时明显已经越界
因此，这两个位置需要单独处理

4）填表顺序：

什么是填表顺序？
很好理解，例如说本题
i位置值得求解，需要前面两个位置的值已经存在才能求解
因此，也就是说在算i位置时，i-1 和 i-2 位置已经填了，已经有值了
所以，在这个题中，我们的填表顺序应该是从前往后，因为后面的值的求解需要前面的值

5）返回值：

因为我们要的是跨过所有台阶，所以这里的返回值是一维数组第n个位置的值
因此，返回值即dp[n]

2、代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //创建dp表（我们要返回n位置，多创建一个位置）
        int n = cost.size();
        vector<int> dp(n+1);

        //初始化（走到0和走到1，是不需要花费的）
        dp[0] = 0;
        dp[1] = 0;
        
        //填表  
        for(int i = 2; i<=n; ++i)
        {
            dp[i] = min((dp[i-1] + cost[i-1]), (dp[i-2] + cost[ i-2 ]));
        }

        //确定返回值
        return dp[n];

    }
};

题二

1137. 第 N 个泰波那契数 - 力扣（LeetCode）

1、算法解析

你自己根据我第一题的过程，自己照着求解一般，然后写出代码。

1、确定状态

确定状态是在干什么？
就是确定状态dp数组中的值代表什么含义
dp表里某个位置值的状态就是题目的解

2、状态转移方程

dp[i] = dp[i-1] + dp[i-2] + ap[i-3];题目都直接给了

3、初始化

保证填表的时候越界
根据状态表示方程进行填表
状态方程是dp[i] = dp[i-1] + dp[i-2] + ap[i-3];
因此当i小于3的时候，越界
因此，初始化状态表，dp[0] = 0;dp[1] = ap[2] = 1;

4、填表顺序

从左往右填表，因为第n个位置的值，需要前面三个值已经计算好。

5、返回值

结果是第n个位置的值
所以，返回值就是dp[n]（因此需要多创建一个位置的空间）
 

2、代码

class Solution {
public:
    int tribonacci(int n) {

        if(n == 0) return 0;
        if(n == 1|| n == 2) return 1;

        //1、创建dp表
        vector<int> dp(n + 1);

        //2、初始化
        dp[0] = 0;
        dp[1] = dp[2] = 1;

        //3、填表
        for(int i = 3; i<=n; i++ )
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        
        //4、确定返回值
            return dp[n];        


    }
};

3、空间优化版本

//空间优化版本
class Solution {
public:
    int tribonacci(int n) {

        if(n == 0) return 0;
        if(n == 1|| n == 2) return 1;

        int a = 0, b = 1, c = 1, d = 0;
        
        for(int i = 3; i <=n;i++)
        {
            d = a+b+c;
            a = b;
            b = c;
            c = d;
            
        }

        return d;
        
    }
};

 题三

面试题 08.01. 三步问题 - 力扣（LeetCode）

1、算法解析

1、确定状态：

定义 dp[i] 数组中的值到底表示什么意思？
很简单，根据题目，就是到达该台阶一共有多少种走法。
我们的目标是求解 dp[n]，即上到第 n 阶台阶的方式数量。

2、状态转移方程：

考虑小孩每次可以走 1 阶、2 阶或 3 阶：

因此，状态转移方程为：
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]

3、初始化：

dp[0] = 1：上到第 0 阶只有一种方式，就是不走任何台阶。
dp[1] = 1：上到第 1 阶只有一种方式，就是从地面直接走一阶。
dp[2] = 2：上到第 2 阶有两种方式，可以走两次一阶或者一次两阶。
为什么初始化这三个位置？因为他们需要前面三个位置的值，如果不初始化，会越界。

4、填表顺序：

从 dp[3] 开始一直填充到 dp[n]。

5、返回值：

返回 dp[n]，因此要多创建一个位置的空间，同时由于结果可能很大，要对 dp[n] 模 1000000007 取余。

2、代码

class Solution {
public:
    int waysToStep(int n) {
        if(n == 1) return 1;
        if(n == 2) return 2;

        // 1、创建dp表
        vector<int> dp(n + 1);
        
        // 2、初始化
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;

        // 3、填表
        for(int i = 3; i<n+1; ++i)
            dp[i] = ((dp[i-1] + dp[i-2]) % 1000000007 + dp[i-3]) % 1000000007;

        // 4、确定返回值
        return dp[n];
        
    }
};

  题四

91. 解码方法 - 力扣（LeetCode）​

1、算法解析

1、确定状态：

定义 dp[i] 数组中的值到底表示什么意思：dp[i]的值，就是以i为结尾的编码串的最多解码方式

2、状态转移方程：

​

因此，状态转移方程为：
dp[i] = dp[i-1] + dp[i-2] 

3、初始化：

为什么初始化这几个位置？因为他们需要前面三个位置的值，如果不初始化，会越界。

4、填表顺序：

从 dp[3] 开始一直填充到 dp[n]。

5、返回值：

返回 dp[n]

2、代码

class Solution {
public:
    int numDecodings(string s) {
    //1、创建dp表
    int n = s.size();
    vector<int> dp(n);

    //只有一位
    dp[0] = s[0] == '0' ? 0 : 1;
    if(n == 1 ) return dp[0];

    //2、初始化
    //根据判断条件进行初始化
    if(s[0] != '0' && s[1] != '0') dp[1]++;
    int m = (s[0] - '0')*10 + (s[1] - '0');//组合编码
    if(m>=10 && m <= 26)
        dp[1] ++;

    //3、填表
    for(int i = 2; i<n; ++i)
    {
        //i位置单独编码
        if( s[i] != '0') dp[i] += dp[i-1];
        //i和i-1位置组合编码
        int x = (s[i-1] - '0')*10 + (s[i] - '0');
        if(x >= 10 && x <= 26) dp[i] += dp[i-2];
    }

    //4、返回值
    return dp[n-1];

    }
};