接下来我们将进行一些稍微高级一点操作,一边学习新东西的同时,也开始对数学、物理等内容的研究。
目录
- 一、项目截图
- 二、涉及内容
- 三、问题设置
- 1. 问题提出
- 2. 验证方案
- 三、做图步骤
- 1. 绘制定点A、B;
- 2. 绘制动点C;
- (1)绘制一个滑动条s1;
- (2)绘制动点C;
- 3. 绘制三角形ABC;
- 4. 任意选两条边绘制中垂线;
- 5. 绘制两个中垂线的交点D;
- 6. 以D点为圆心绘制过A点的圆;
- 7. 滑动C点查看变化;
- 四、问题结论
- 四、正确性检查
- 五、文章最后
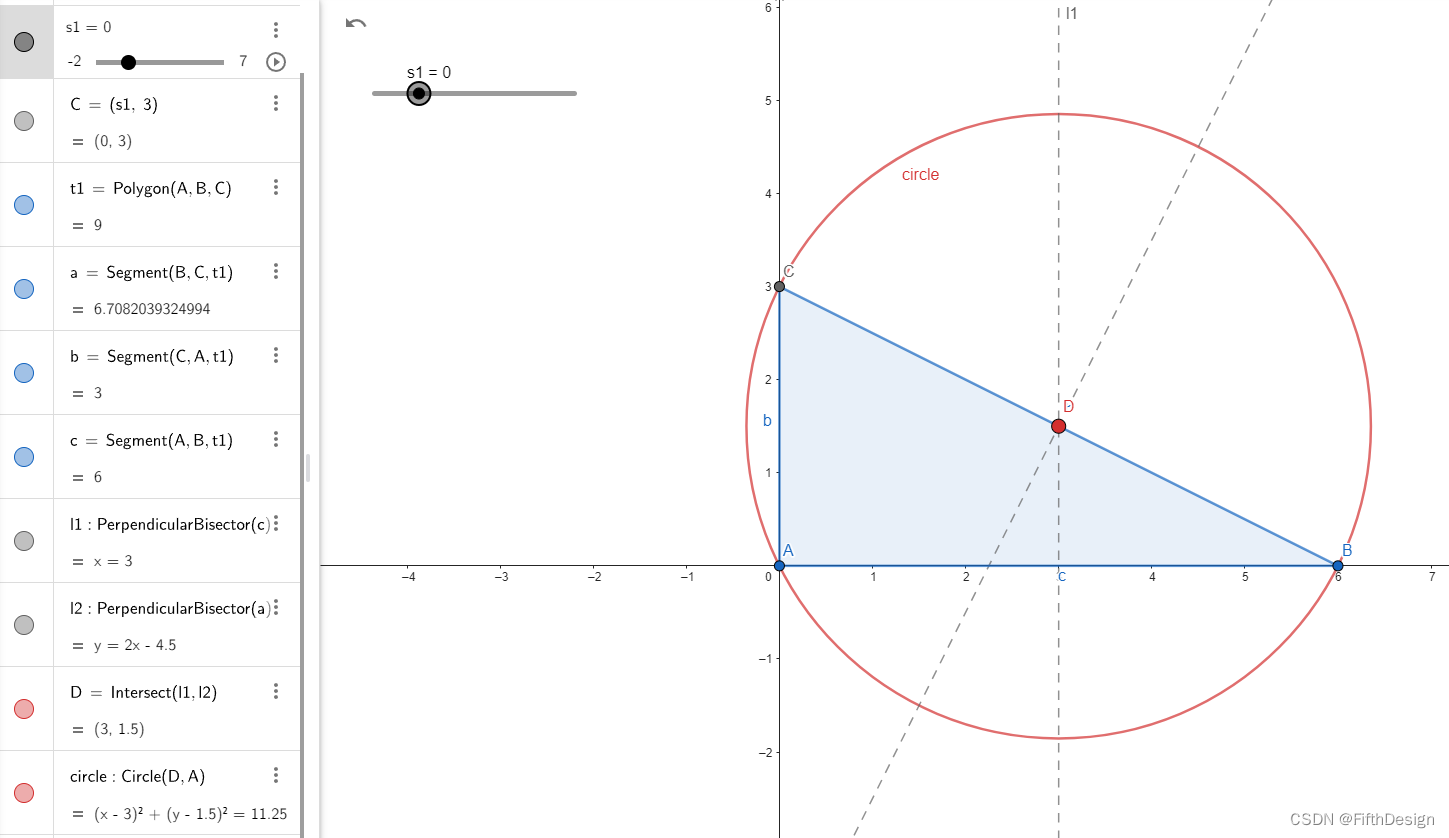
一、项目截图
二、涉及内容
- 设置可以定点和动点;
- 制作三角形;
- 绘制边的中垂线;
- 获取线的交点;
- 过一点绘制圆;
- 变化动点,查看三角形外接圆情况;
三、问题设置
1. 问题提出
三角形外接圆的圆心是否可以位于三角形的外部?
2. 验证方案
尺规作图,动态实验。
三、做图步骤
1. 绘制定点A、B;
A=(0,0)
B=(6,0)
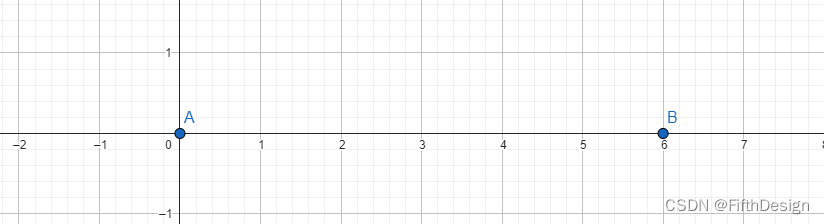
所谓的定点就是固定不动的点
2. 绘制动点C;
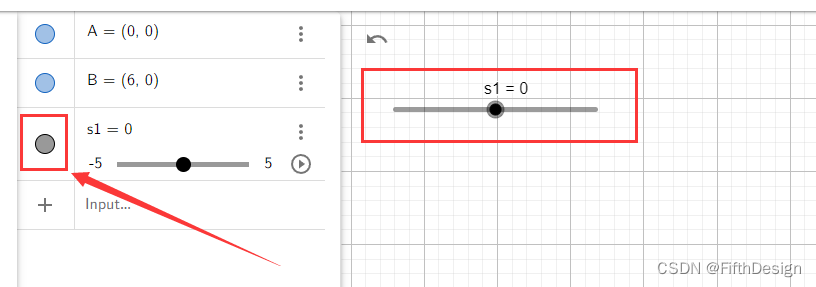
(1)绘制一个滑动条s1;
s1=0
直接写这个就可以(还有很多其他方式,我们后边一步步讲),然后会发现算式输入框下边出现这个,说明滑动条已经建立起来了。

注意,滑动条建立后默认是隐藏状态,需要把前边的小圆点击一下,就可以了。
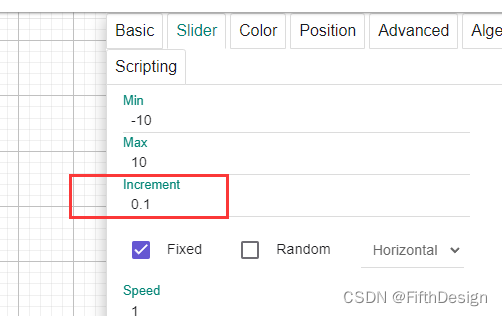
如果这个滚动条的数字范围不合你意,可以双击窗口中的滑动条(或者选中后Ctrl + E),就可以打开设置面板,在这里修改就可以了,我这里修改成了(-10,10)(或者直接在算式栏点击一下输入就可以了,方式很多,可以自己探索下)

在这里可以修改步进值,我这里设置的是0.1(比较平滑)(其他设置可以先自己试试,当然后边文章中都会涉及)
(2)绘制动点C;
C=(s1,3)
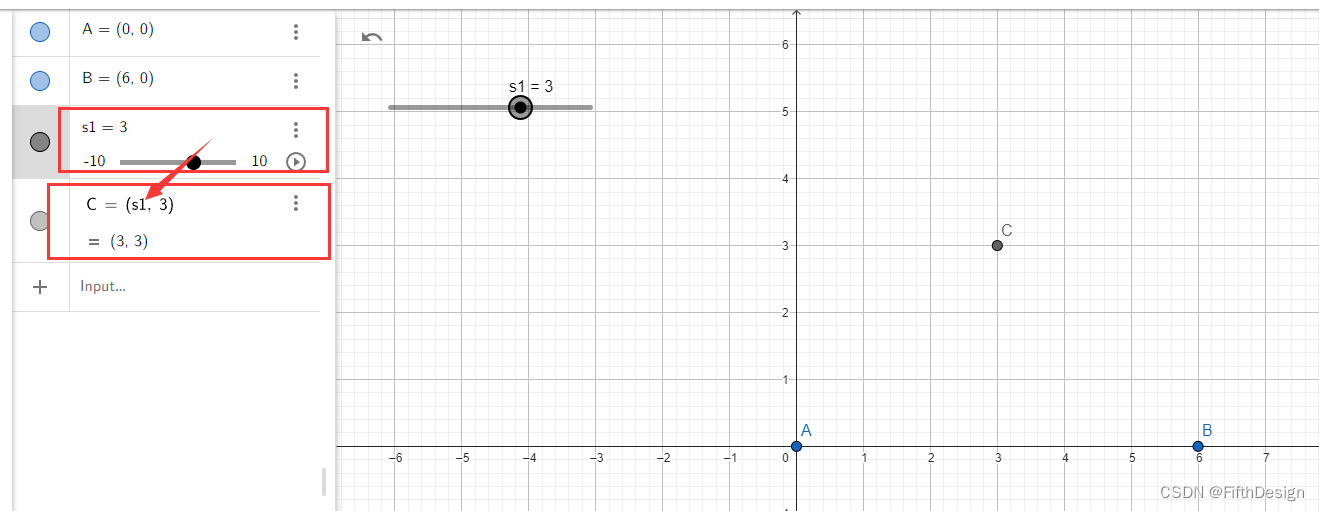
注意,这里就开始高端操作了,因为滑动条返回的是一个数值,所以我就直接将滑动条的变量作为点C的x,这样点C就可以随着滑动条的变化产生移动(这种方式是整个GeoGebra的灵魂之一)
3. 绘制三角形ABC;
t1=Polygon(A,B,C)

输入完三角形后下边会自动出来三条边a、b、c
4. 任意选两条边绘制中垂线;
l1: PerpendicularBisector(c)
l2: PerpendicularBisector(a)
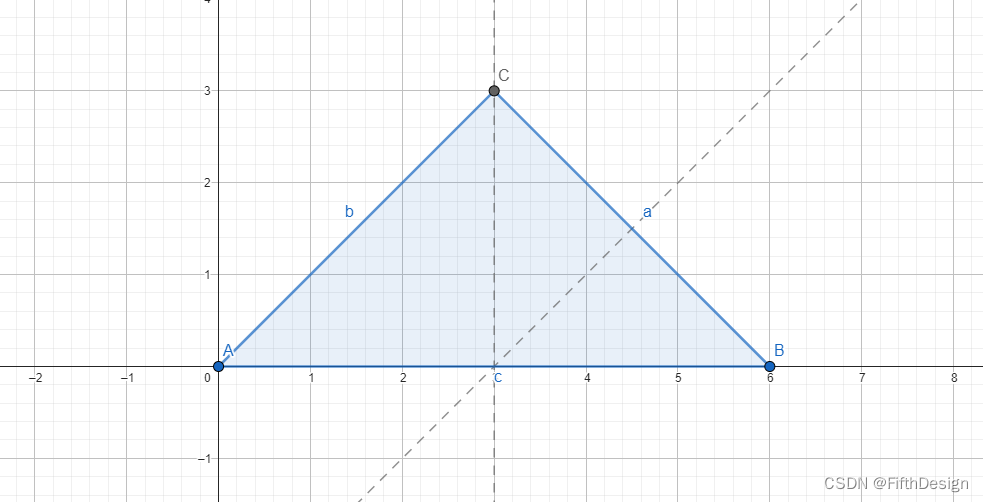
这里我选择的是a和c
5. 绘制两个中垂线的交点D;
D=Intersect(l1,l2)
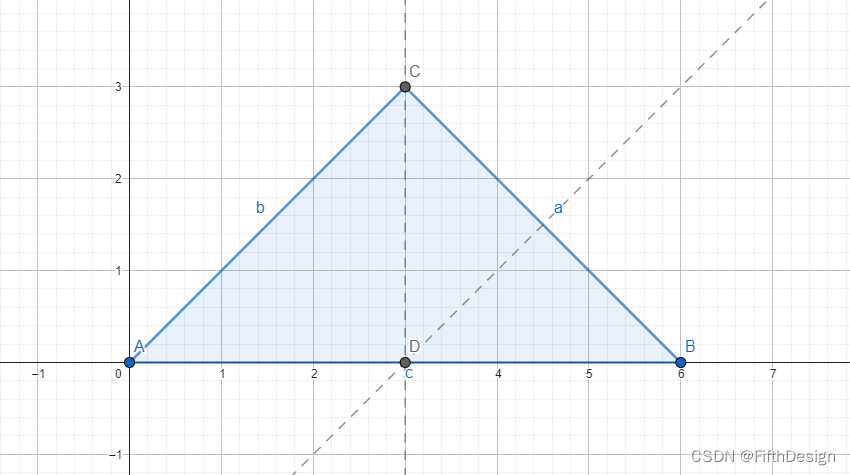
这个命令在前面用过很多次,就不赘述了(建议跟着文章的序号逐次阅读)。
6. 以D点为圆心绘制过A点的圆;
circle: Circle(D,A)
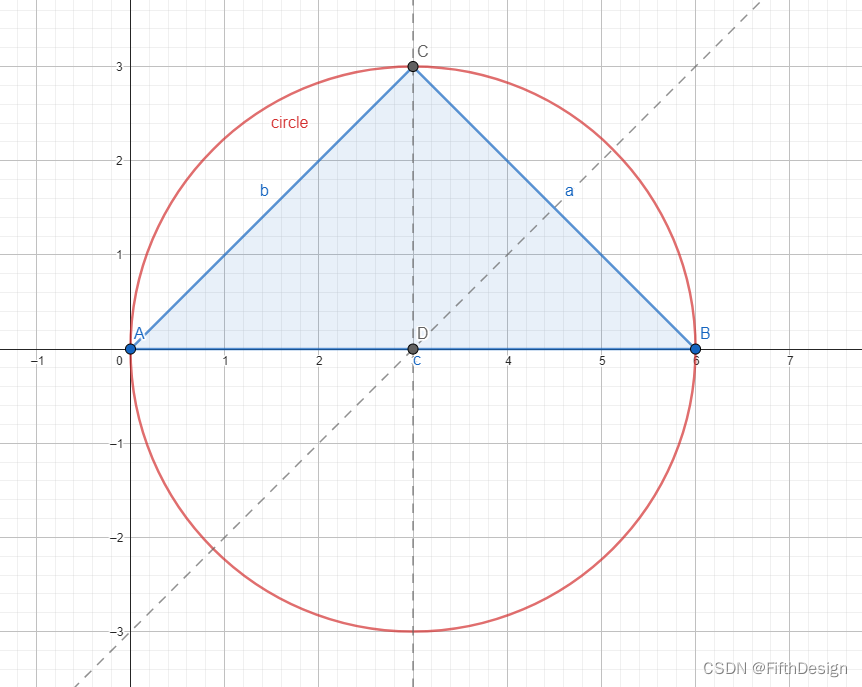
7. 滑动C点查看变化;
记得滑动条这里有个播放按钮不?就是这里
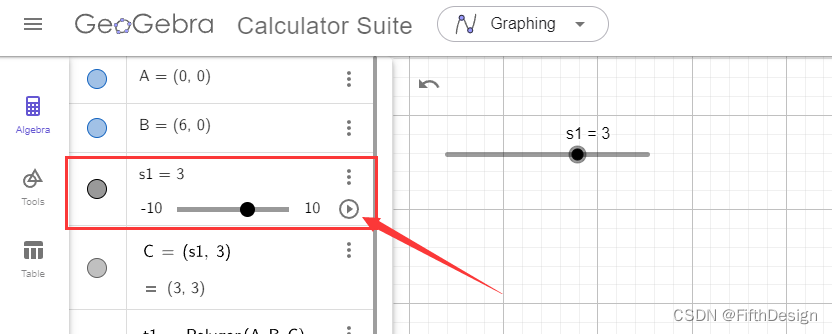
对的,点击一下看看效果(不得不说滑动条范围有点大,图形都超出工作区范围了,建议修改为(-2,7)):

注意看点D,这答案就很明显了。
四、问题结论
- 三角形外接圆的圆心可以在三角形外部;
- 锐角三角形的外接圆圆心位于三角形内部;
- 钝角三角形的外接圆圆心位于三角形外部;
- 直角三角形的外接圆圆心位于三角形的斜边上;
当然我最后三条结论有点空口无凭啊,不过你可以将三角形的三个角标注上,这样就可以看到角度的变化了。
四、正确性检查
小心驶得万年船,还是那种方式,任意找一个元素,拖动,看看全局能不能一起动,如果可以就说明没有问题。
五、文章最后
若有任何问题都可以在这个铺子问客服,也会有资源相送,GeoGebra、PPT、平面动画、3D动画等各种技术都可以,祝好!