结论
国内同行对chatgpt的认识是不够的,太轻视这个模式的颠覆性认知
chatgpt是对思维过程的仿真,rlhf过程就是通过强化学习方式在利用人思维过程训练模型
chatgpt比搜索更通用化,搜索是对单个点信息的匹配,chatgpt是对思维链一个序列数据的匹配,所以通用性和能力更强
chatgpt绝对不是简单的训练数据量大打来的所谓涌现效果,数据量大是基础,但是对思维模式的仿真才是它强大的原因
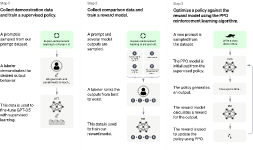
例子
营销文本生成:
选择主题
问题:如何生成对女性有吸引力的营销文案,帮忙生成些主题和关键词
答:
选择关键词
问题:请从{稳健,利润、增长,美丽,好心情,人生......}词列表中,选出10个最优的词来做适合女性基金营销文案生成
答:
生成模版
问题:请用【稳健、利润、增长.....】中任意三个词做组合,产出适合bart模型文案生成的模版
答:
生成句子
问题:请用‘[MASK]稳健[MASK]增长[MASK][MASK]‘模版,生成十句适合女性的差异化基金营销文案
答:
通顺度检测
问题:{'好基金稳健,年收益持续增长','好稳健好增长好好好'......}列表中通顺的句子有哪些
答:
多样性改写
问题:请把'好基金稳健,年收益持续增长'改写10句,适合不同年龄、学历、工作经验女性的基金营销文案
答:
句子挑选
问题:请从{'好基金稳健,年收益持续增长','好稳健好增长好'......}句子中选出10句,作为年底**货币基金营销的文案,要求句子间差异度性最大,句子押韵文风优美
答:
输出
问题:{'好基金稳健,年收益持续增长','好稳健好增长好'......}句子对**人群匹配度有多高,年轻高职高学历未婚用户会最喜欢哪条文案
答:
思考
把人类解决问题的过程,人类解决问题时的思维链做仿真。把人类思维链路作为训练数据,作为强化学习的建模绝对是一次更接近智能本质的探索。
搜索是点匹配全域数据
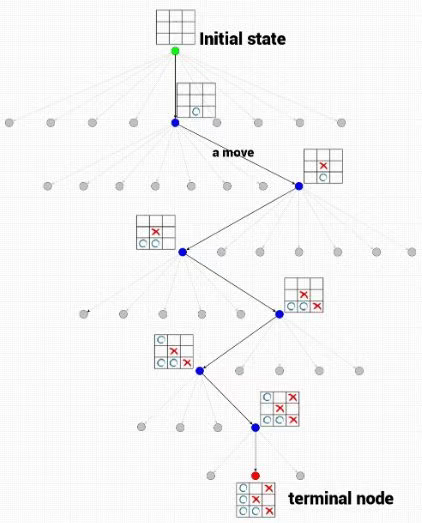
而chatgpt是一个点选择有限思维链路
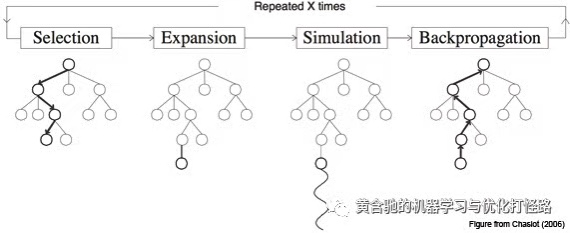
然后通过输入交互数据逐步递进下一个决策状态
思维链路是有限的 每个思维链路下可选状态也是有限的 有点类似多步马尔可夫树搜索
所以chatgpt学习的是思维链
然后通过模型检索在指定链路下的可选集合
并且会通过用户交互信息逐步修正精准答案
举个例子:
写文章,有两个思维链模式(可以是显式的也可能是隐式的),
主题——大纲——每段论据——论据支撑——论据衔接文字
主题——关键——关键词衍生段落——段落句子——句子衔接顺序
用户在输入写作命令+写的信息后,chatgpt隐或显的选择了一个思维链,然后用有限的‘写的信息’写出一些东西,然后把检索到的信息案思维链一步一步扩展出可能的门特卡洛决策树,直到得到最后答案。
所以rlhf训练学习的是思维链,人做事思考的思维链其实是有限的,所以在有限信息下经过这种链+检索方式生产的内容和答案是有逻辑的。但是对于多轮对话,这个问题chatgpt还是没能很好解决,这应该设计到长期记忆和分区记忆信息,现在模式还不具备这种更高级别能力