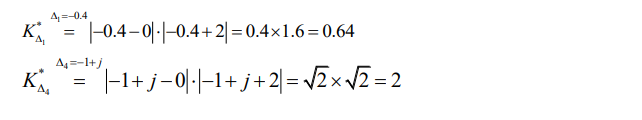目录

根轨迹的基本概念：

根轨迹的概念：当开环系统某一参数从 0 到∞变化时，闭环极点在S 平面上变化所描绘出的轨迹。

闭环零极点与开环零极点之间的关系：

根轨迹方程：

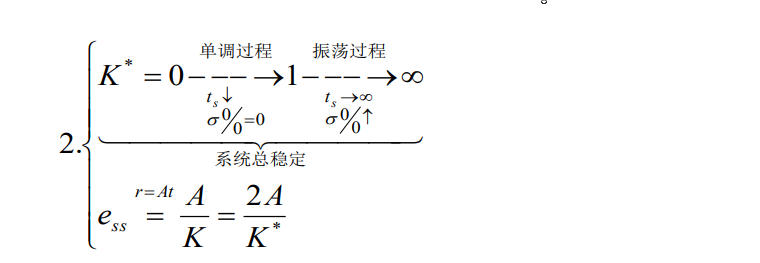
 开环增益于根轨迹间的关系：

---

闭环系统的性能由闭环零极点分布决定。当开环传递函数中某个参数化时，闭环系统特征方程的系数也相应变化，闭环极点也要改变（解根难）。研究闭环极点随开环某参数变化而变化的规律，进而讨论闭环系统性能的变化趋势，是具有理论和实际工程意义的课题。（调参、设计等）。

根轨迹的特点：

● 图解法，简单；

● 特别适用于研究当系统的开环参数变化时，系统性能的变化趋势；

● 近似方法，不十分精确。

根轨迹的基本概念：

根轨迹的概念：当开环系统某一参数从 0 到∞变化时，闭环极点在S 平面上变化所描绘出的轨迹。

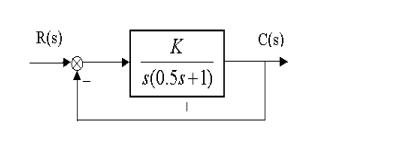
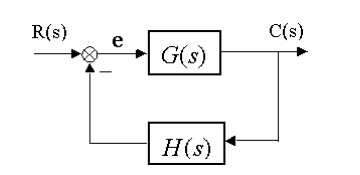
系统如图：

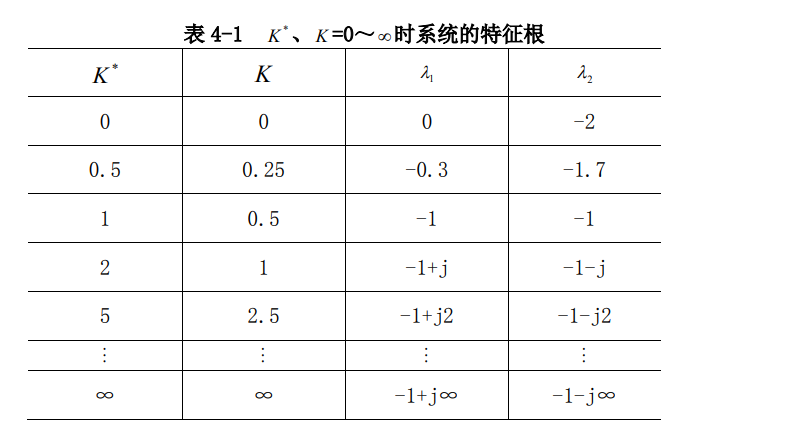
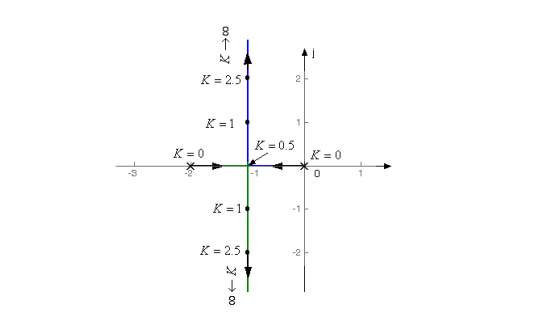
闭环零极点与开环零极点之间的关系：

系统如图：

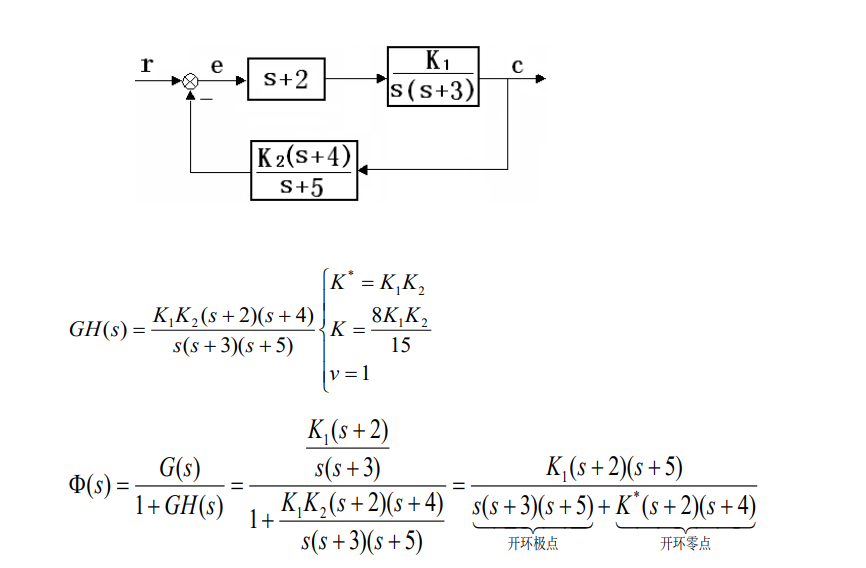
结论：

●闭环零点=前向通道的零点+反馈通道的极点（不随 * K 变化，易得到，不必专门研究。）

● 闭环极点与开环零点，开环极点和根轨迹增益 * K 都有关系（需专门研究）。

---

根轨迹方程：

如系统：

 

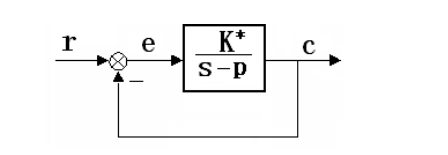
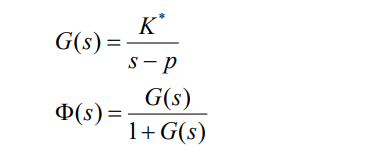
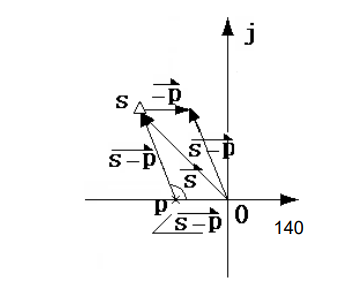
 开环增益于根轨迹间的关系：

● 任一点 S,总可以有一个 * K 与之对应，满足模值条件，但它不一定在根轨迹上（不一定满足相角条件）

● 满足相角条件的 S，也一定有对应的 * K 使之满足模值条件，所以相角条件是判定 S 在不在根轨迹上的充要条件

● 当 S 满足相角条件时，它一定在根轨迹上，所对应的 * K 值，由模值条件确定