文章目录
- 引言
- 新作
- 爬楼梯
- 个人实现
- 参考实现
- 杨辉三角
- 个人实现
- 参考实现
- 打家劫舍
- 个人实现
- 参考实现
- 完全平方数
- 个人实现
- 参考实现
- 总结
引言
- 回家以来,和朋友的聚会暂时告一段落了,后面就准备闭关,继续准备秋招了,不能在浪费时间了。
- 加油,虽然我的实习效果不怎么样,但是秋招加油好好准备总是有效果的。
新作
爬楼梯
-
题目链接

重点 -
有两种爬楼梯得方式,分别是爬一步和爬两步两种策略,动态规划可以实现
-
n最大是45
个人实现
- 状态计算方程应该是f[i] = f[i - 1] + f[i - 2];
- 这道题是很基础的动态规划题目,总体实现起来比较简单。
class Solution {
public:
int f[50];
int climbStairs(int n) {
f[0] = 1;
for (int i = 1; i <= n; ++i) {
f[i] += f[i - 1] ;
if (i >= 2) f[i] += f[i -2];
}
return f[n];
}
};
参考实现
- 声明vector的时候可以指定对应的vector的长度,然后通过该种方式可以进一步节省内存。
class Solution {
public:
int climbStairs(int n) {
vector<int>f(n + 1);
f[0] = 1;
f[1] = 1;
for (int i = 2; i <= n; i ++ )
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
};
杨辉三角
- 题目链接
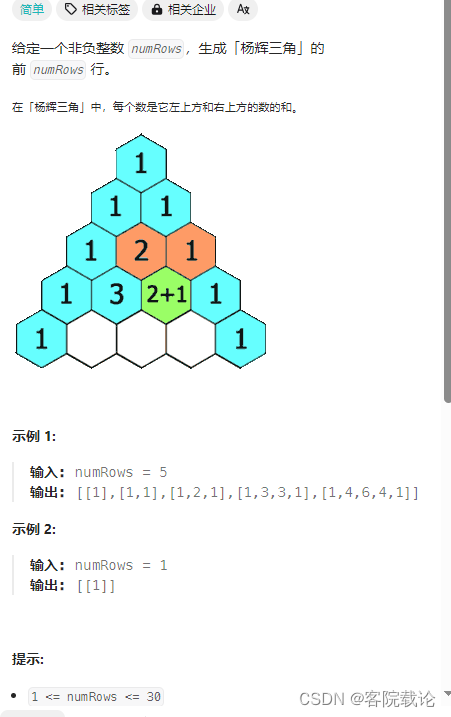
注意点
- 生成杨辉三角的前n行
- 杨辉三角是当前数字等于肩膀上两个数字之和,所以如何获取肩膀上的两个数的具体的值十分重要。
- 同时判定每一行结束的位置也十分重要。
- 开头和末尾的数字一定是的1
个人实现
- 使用动态规划实现,但是如何定位具体的数字的坐标?
- f[i][j] = f[i - 1][j - 1] + f[i - 1][j]
问题
- 在实现过程中,遇到一个问题,这个映射关系还是蛮混乱的,如何写才能更加简单清晰明了,不用像之前一样,每一次都要减去对应的值。
注意
- 这里第二重小循环遍历的时候,终止条件是i,并不是n,这里写错了好几次,所以会出问题。
class Solution {
public:
vector<vector<int>> generate(int n) {
vector<vector<int>> res = {{1},{1,1}};
if(n == 1) return {{1}};
if(n == 2) return res;
for(int i = 3;i <= n;i ++){
// 这样写是否可以成功?会不会自动加上一个数据?
res.push_back({});
res[i - 1].push_back(1);
for(int j = 2;j < i; j++ ){
// cout<<j<<",:"<<res[i -2].size()<<endl;
// cout<<res[i -2][j - 1]<<endl;
res[i - 1].push_back(res[i - 2][j - 2] + res[i -2][j - 1]);
}
res[i - 1].push_back(1);
}
return res;
}
};
参考实现
参考分析
- 下述是y总的代码,对于每一次都需要进行变换的二次数组,可以使用一个中间变量进行保存,这样写就方便很多。
- 直接获取数组的最后一个vector,然后再新建一个vector,然后改变新建的vector,生成的新的vector数组。
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> res;
if (!numRows) return res;
res.push_back(vector<int>(1, 1));
for (int i = 1; i < numRows; i ++ )
{
vector<int> &last = res.back();
vector<int> temp;
temp.push_back(1);
for (int i = 0; i + 1 < last.size(); i ++ )
temp.push_back(last[i] + last[i + 1]);
temp.push_back(1);
res.push_back(temp);
}
return res;
}
};
作者:yxc
链接:https://www.acwing.com/solution/content/209/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处
打家劫舍
题目链接

注意
- 如果同时闯入相邻房屋就会触发报警==》不能同时选择相邻的两个元素
- 求取最高的金额
个人实现
-
这道题就是一个标准的状态DP,而且和之前的大盗阿福很像,之前的分析链接如下
-
股票买卖状态机
-
股票买卖状态机2
-
这里获取对应的状态即可,每一个房屋只有两个状态,取或者不取,然后如果上一个取了,这一次就不能取
-
f[i] = max(f[i - 1],f[i - 1] + w[i])
- 感觉有点小问题,这个状态转移方程有点问题,上一个取了,我怎么知道上一个取了?我需要管吗?很明显是需要的,因为上一个状态是会影响当前的状态,但是怎么表示?
- 两个矩阵吗?明显不是的,想想之前的股票买卖问题,我可以定义两个状态,相当于是两个状态转移方程
- f[i][0]表示第i个房屋已经抢了
- f[i][1]表示第i个房屋没有被抢
-
那么这样定义之后,这种状态方程就简单很多了。具体状态转移方程如下
- f[i][0] = max(f[i-1][1] + w[i])
- 当前房屋被抢了,只有一种可能会变成当前状态,就是上一个房屋没有被抢
- f[i][1] = max(f[i-1][1] ,f[i-1][0] ),总共有两种情况
- 上一个房屋被抢了
- 上一个房屋没有被抢
- f[i][0] = max(f[i-1][1] + w[i])
具体实现如下
class Solution {
public:
int rob(vector<int>& n) {
vector<vector<int>> f;
// 更新一下f[0][0]
f.push_back({n[0],0});
int l = n.size();
for(int i = 1;i < l;i ++){
f.push_back({0,0});
cout<<f[i][0]<<" "<<f[i][1]<<endl;
// 第i个家,抢了
f[i][0] = f[i-1][1] + n[i];
// 第i个家,不抢
f[i][1] = max(f[i-1][0],f[i-1][1]);
}
return max(f[l-1][1],f[l-1][0]);
}
};
参考实现
- 我写的还是太复杂冗余了,看看这个代码,写的多简洁。
- 既然同时申请二维的vector是一件困难的事情,为什么不直接申请两个一维的数组,这样效果不是更好吗?
- 而且刚才还在对数组的索引产生疑惑,不知道怎么处理更好,为什么不直接从第二天开始索引?
int rob(vector<int> nums)
int n = nums.size();
vector<int> f(n + 1),g(n + 1);
for(int i = 1;i <= n;i ++){
f[i] = g[ i -1] + nums[i -1];
g[i] = max(f[i - 1],g[i - 1]);
}
return max(f[n],g[n]);
}
完全平方数
- 题目链接

重点 - 完全平方数:自己和自己的乘积的和
- 和为n 的完全平方数的最小数量
个人实现
- 这道题应该不是上一题一样的状态DP,回顾一下我们经历过那几个类型的DP
- 背包问题
- 数字三角问题
- 树形DP
- 单调队列
- 最大上升子序列
- 状态压缩DP
- 状态DP
- 区间DP
- 从目前来看,感觉很像是一个完全背包问题,然后计算的是最小值,状态转移矩阵如下
- f[i][j]
- i表示第几个完全平方数
- j表示当前目标值
- f[i][j] = f[i][k] k为第i个物体不断重复k次,知道超过背包容量
- f[i][j]
class Solution {
public:
int numSquares(int n) {
// 创建并保存每一个需要遍历的变量
vector<int> exp;
for(int i = 1;i*i <= n;i ++) {
exp.push_back(i*i);
if(i * i == n) return 1;
}
// 创建需要保存数据的二维矩阵
int l = exp.size();
// int f[l + 1][n + 1];
// memset(f,INT_MAX,sizeof(f));
vector<vector<int>> f(l + 1);
for(int s = 0; s <= n;s ++)
// f[0][s] = s;
f[0].push_back(s);
for(int i = 1;i < l;i ++){
for(int s = 0; s <= n;s ++){
f[i].push_back(INT_MAX);
// 当前的数字不放任何物体
f[i][s] = f[i - 1][s];
for(int j = 1 ;j * exp[i] <= s; j ++ ){
// 靠,这里看错了,调试了半天,居然是结果弄错了!
// cout<<"exp[i]:"<<exp[i]<<" i:"<<i<<" s:"<<s<<" j"<<j<<endl;
// cout<<f[i - 1][s - j * exp[i]]<<endl;
// cout<<f[i][s]<<endl;
f[i][s] = min(f[i][s] , f[i - 1][s - j * exp[i]] + j);
}
}
}
return f[l - 1][n];
}
};
- 很明显,这里要使用公式转换和滚动矩阵进行优化,这里的代码我会推导,但是没有时间了,直接看参考代码吧
参考实现
- 下面这个代码太不寻常了,肯定是使用了我不知道是什么数学推理,或者没有发现的规律,已经不是动态规划l了。

- 当真的是的!
class Solution {
public:
bool check(int x) {
int r = sqrt(x);
return r * r == x;
}
int numSquares(int n) {
if (check(n)) return 1;
for (int a = 1; a <= n / a; a ++ )
if (check(n - a * a))
return 2;
while (n % 4 == 0) n /= 4;
if (n % 8 != 7) return 3;
return 4;
}
};
动态规划问题二
有一个关键的集合表示方法,就是当前的集合可以使用一个平方数进行表示,然后剩下的数字能不能使用一个平方和数字使用保存。
class Solution {
public:
int numSquares(int n) {
vector<int> f(n + 1);
for (int i = 1; i <= n; i++) {
int minn = INT_MAX;
for (int j = 1; j * j <= i; j++) {
minn = min(minn, f[i - j * j]);
}
f[i] = minn + 1;
}
return f[n];
}
};
作者:力扣官方题解
链接:https://leetcode.cn/problems/perfect-squares/solutions/822940/wan-quan-ping-fang-shu-by-leetcode-solut-t99c/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
总结
- 今天状态还行,上午做的两道简单题基本上都是在限定时间内做出来的。
- 虽然之前浪费了很多时间,但是这些浪费也不是完全无用的,至少到现在,做的三道动态规划题目,都能够在规定的二十五分钟内完成,还是有用的。
- 今天晚上两道中等题,都是做出来了,第一道题AC了,第二道题大部分样例都是AC的,但是超时了。 后续可以在修改。
- 今天少做了一题,明天继续加油!!