2019-ICML-Towards Graph Pooling by Edge Contraction

Paper: https://graphreason.github.io/papers/17.pdf
Code: https://github.com/Jiajia43/pytorch_geometric
通过边收缩实现图池化
池化层可以使GNN对抽象的节点组而不是单个节点进行推理,从而增加其泛化潜力。为此,作者提出了一个依赖于边缘收缩概念的图池层:EdgePool 学习局部和稀疏池化转换。实验表明,EdgePool可以集成到现有的GNN架构中,而不会增加任何额外的损失或正则化。
模型
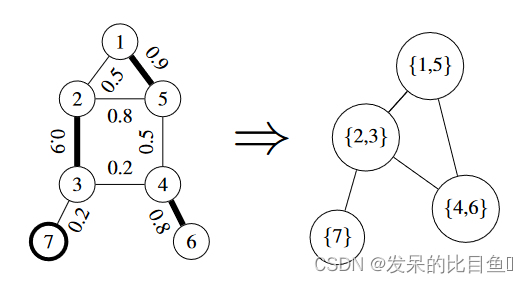
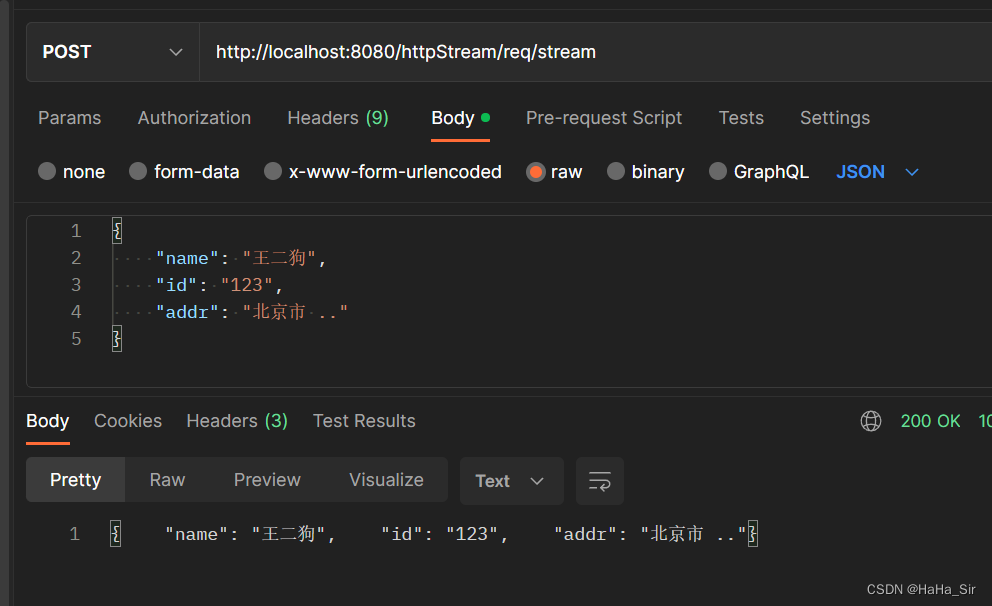
边缘池:计算图形中每条边的分数(左)。这些边按其分数的顺序收缩(edges {1, 5}, {4, 6}, {2, 3};所选边以粗体显示),已属于池边的节点将被忽略(p.ex. edges {2, 5})。保留收缩节点之间的边,保留剩余节点(节点 7)。生成的图形(右)是合并表示。
定义图 G = ( V , E ) G = (V,E) G=(V,E),其中每个 v v v 节点都有 f f f 特征 V ∈ R v × f V \in R^{v×f} V∈Rv×f 。边表示为没有要素权重的结点对。边表示为没有要素权重的结点对。虽然图卷积函数采用固定图并且只转换节点特征,但池化函数也会转换图并减少节点数量。生成的图形是输入图形的粗略表示。
边收缩
直观地说,边缘收缩意味着合并两个节点。收缩边 e = { v i , v j } e = \{v_i, v_j\} e={vi,vj} 引入了新的顶点 v e v_e ve 和新边,使得 v e v_e ve 与所有节点相邻 v i v_i vi 或 v j v_j vj相邻。 v i v_i vi、 v j v_j vj 及其所有边将从图形中删除。这被写为 G/e,每次这样的收缩都会将图中的节点数减少1。
由于边收缩是可交换的,我们也可以定义一个边集收缩 G / E ′ G/E′ G/E′,其中 E ′ = { e 1 , . . . , e n } ∈ E E' = \{e_1,...,e_n\} \in E E′={e1,...,en}∈E。避免收缩入射到同一节点的边缘。
边缘收缩池
该方法选择一组边,然后使用边收缩来生成一个新图。如何选择要池化的边以及如何组合节点特征。通过自由选择计算此值的函数。首先将每条边的原始分数计算为级联节点特征的简单线性组合,即对于从节点
i
i
i 到节点
j
j
j 的边,将原始分数
r
r
r 计算为

其中
n
i
n_i
ni 和
n
j
n_j
nj 是节点特征,
W
W
W 和
b
b
b 是学习参数。
为了使梯度流分数,作者使用门控,并将组合的节点特征乘以边缘分数:

实验
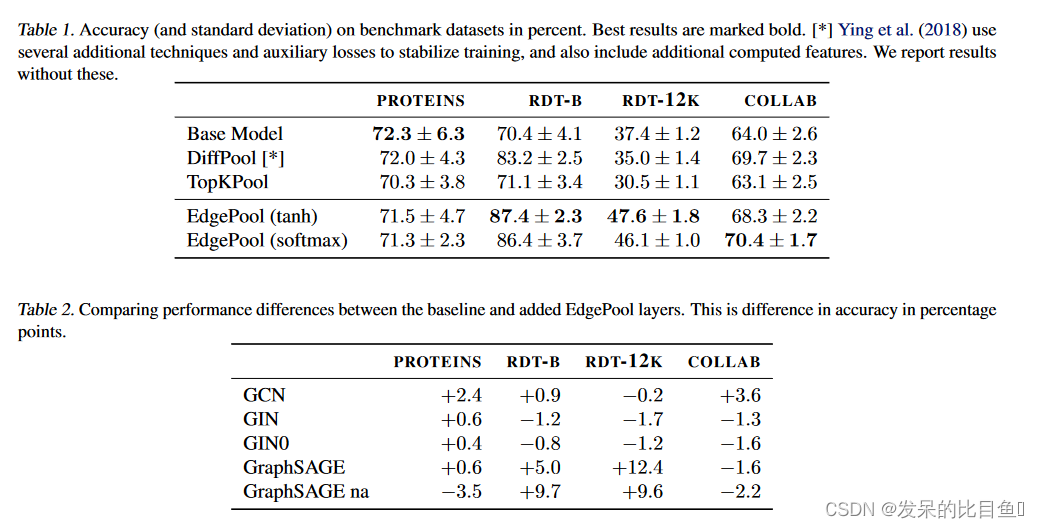
如表 1 中的结果所示,EdgePool 在四个数据集中的三个数据集上都优于基线和两种替代池化方法。
如表 2 中的结果所示, EdgePool 的性能提升取决于所使用的卷积层和数据集,但取决于性能。由于图的大小和结果的巨大变异性而忽略蛋白质,两种 GIN 变体都没有从引入池化中受益。