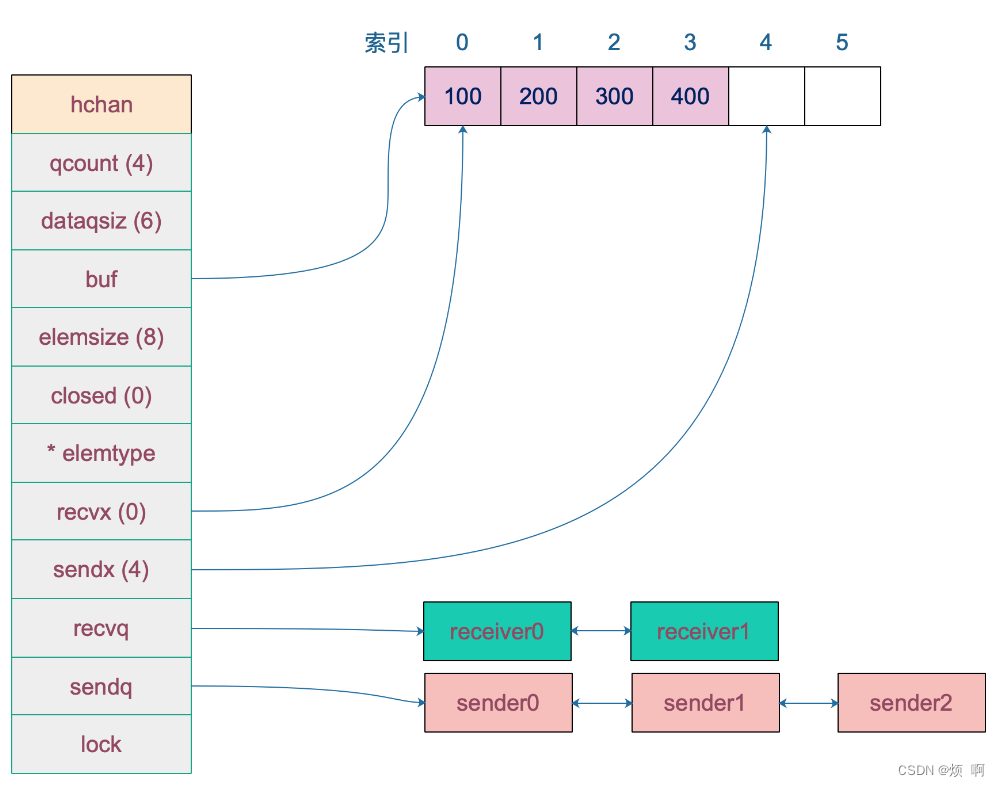
斜率优化DP——AcWing 303. 运输小猫

news2024/11/26 5:36:54

斜率优化DP

定义

斜率优化DP（Slope Optimization Dynamic Programming）是一种高级动态规划技巧，用于优化具有特定形式的状态转移方程。它主要应用于那些状态转移涉及求极值（如最小值或最大值）的问题中，通过分析状态转移函数的斜率特性，将原本需要进行多次比较的操作转化为对斜率的管理，从而减少计算量。斜率优化的核心在于利用函数的单调性，通过维护一个数据结构（如单调队列）来避免重复计算，达到优化的目的。

运用情况

最优化问题：当动态规划的状态转移涉及求解最小值或最大值，且转移方程可表达为线性或近似线性关系时。
序列问题：例如，在序列中选择一段区间，使得区间内满足某种条件的子序列和最大或最小。
费用最小化问题：如求解完成某任务序列的最小花费，其中选择下一个任务的成本可能依赖于之前的选择。
具有特殊结构的问题：如某些问题的状态转移可以通过分析状态间的关系转换为斜率的比较和更新。

注意事项

状态和转移方程：明确问题的状态定义和状态转移方程，确保它们适合斜率优化。
单调性分析：分析状态转移函数的斜率变化，确定如何维护一个单调队列或其他数据结构来避免无效计算。
边界处理：注意处理状态转移的边界条件，特别是状态转移开始和结束时的特殊情况。
数据结构选择：根据问题的具体情况选择合适的数据结构（如单调队列）来维护关键信息。
复杂度控制：确保斜率优化后的时间复杂度优于原始DP，避免过度优化导致的复杂度上升。

解题思路

理解问题：首先，深入理解问题背景和求解目标，识别出问题是否适合斜率优化。
状态定义：定义合适的DP状态和状态转移方程，注意状态转移应能表达为某种极值问题。
斜率分析：分析状态转移方程中涉及的变量关系，识别出与“斜率”相关的模式，如线性函数、单调性等。
设计优化策略：根据斜率特性设计数据结构（通常是单调队列）来维护中间状态，避免重复计算。
实现代码：编写代码实现动态规划过程，同时集成斜率优化机制，注意正确处理边界和特殊情况。
验证与优化：测试代码，确保正确性，并根据实际情况调整优化策略以进一步提高效率。

AcWing 303. 运输小猫

题目描述

AcWing 303. 运输小猫 - AcWing

运行代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010, M = 100010, P = 110;

int n, m, p;
LL d[N], t[N], a[N], s[N];
LL f[P][M];
int q[M];

LL get_y(int k, int j)
{
    return f[j - 1][k] + s[k];
}

int main()
{
    scanf("%d%d%d", &n, &m, &p);

    for (int i = 2; i <= n; i ++ )
    {
        scanf("%lld", &d[i]);
        d[i] += d[i - 1];
    }

    for (int i = 1; i <= m; i ++ )
    {
        int h;
        scanf("%d%lld", &h, &t[i]);
        a[i] = t[i] - d[h];
    }

    sort(a + 1, a + m + 1);

    for (int i = 1; i <= m; i ++ ) s[i] = s[i - 1] + a[i];

    memset(f, 0x3f, sizeof f);
    for (int i = 0; i <= p; i ++ ) f[i][0] = 0;

    for (int j = 1; j <= p; j ++ )
    {
        int hh = 0, tt = 0;
        q[0] = 0;

        for (int i = 1; i <= m; i ++ )
        {
            while (hh < tt && (get_y(q[hh + 1], j) - get_y(q[hh], j)) <= a[i] * (q[hh + 1] - q[hh])) hh ++ ;
            int k = q[hh];
            f[j][i] = f[j - 1][k] - a[i] * k + s[k] + a[i] * i - s[i];
            while (hh < tt && (get_y(q[tt], j) - get_y(q[tt - 1], j)) * (i - q[tt]) >=
                (get_y(i, j) - get_y(q[tt], j)) * (q[tt] - q[tt - 1])) tt -- ;
            q[ ++ tt] = i;
        }
    }

    printf("%lld\n", f[p][m]);

    return 0;
}

代码思路

输入处理:
- 首先读入山的数量 n、猫的数量 m、饲养员的数量 p。
- 然后读入每两座相邻山之间的距离，并累加得到从1号山到每座山的总距离 d[]。
- 对于每只猫，读入它停留的山的编号 h 和停止玩耍的时刻 t，并计算出相对于1号山的等待时间差 a[i] = t[i] - d[h]。
- 对这些等待时间差进行排序，同时计算累积和 s[]。
动态规划初始化:初始化二维数组 f[j][i] 来存储前 i 只猫被前 j 个饲养员接走的最小等待时间总和。这里 f[j][0] = 0，表示没有猫时等待时间为0。
单调队列优化动态规划:
- 使用单调递减的队列 q[] 来存储可能成为最优解的状态索引。队列中的元素代表当前考虑的猫的下标。
- 遍历每增加一个饲养员 (j 从1到 p) 的情况，对于每只猫 (i 从1到 m)，计算将其加入到当前饲养员的最优解中需要增加的等待时间。
- 通过维护队列保证每次选择的都是可能产生最小等待时间的猫的组合。队列中的更新基于斜率（即增加一个猫带来的收益变化）来进行，确保队头总是最优解的一部分。
- 计算 f[j][i] 时，利用队列中的信息避免重复计算，实现状态转移的优化。
输出结果:最终答案存储在 f[p][m] 中，即所有猫被 p 个饲养员接走的最小等待时间总和。

改进思路

内存优化:当 M 和 P 的值较大时，f[P][M] 的空间复杂度可能较高。可以考虑滚动数组或者只保留必要的状态来减少空间使用。例如，由于状态转移只与前一状态有关，可以只保留两行或一维数组来交替存储上一行和当前行的状态。
细节优化:在计算斜率时，直接计算斜率可能导致浮点运算，影响效率和精度。可以通过比较差值而非直接计算斜率来优化，即比较 (f[j-1][k] - f[j-1][k-1]) 与 (a[k] - a[k-1]) 来判断单调性，避免浮点运算。
输入处理的效率:对于大数组的读入，可以考虑使用更快的IO方式，如 scanf 替换为 read 加缓冲读取，或者使用 ios::sync_with_stdio(false) 禁用C++标准库与C标准库的同步，提升读写速度。
避免重复计算:确认在计算斜率和更新状态时，是否有进一步的重复计算可以避免。例如，是否可以通过更精细的数据结构或额外的变量来避免某些全局查找或重复的计算过程。
代码可读性和维护性:
- 添加更多的注释，特别是对于算法核心逻辑和复杂的数据结构操作部分，提高代码的可读性和后期维护的便捷性。
- 函数化拆分复杂的逻辑，比如将单调队列的维护、状态转移逻辑封装成单独的函数，使代码结构更加清晰。
性能测试与瓶颈分析:实施性能测试，确定程序的瓶颈所在，可能是I/O操作、内存访问、或是特定的计算环节。根据测试结果，针对性地进行优化。