每日算法-插值查找

news2025/1/15 6:31:39

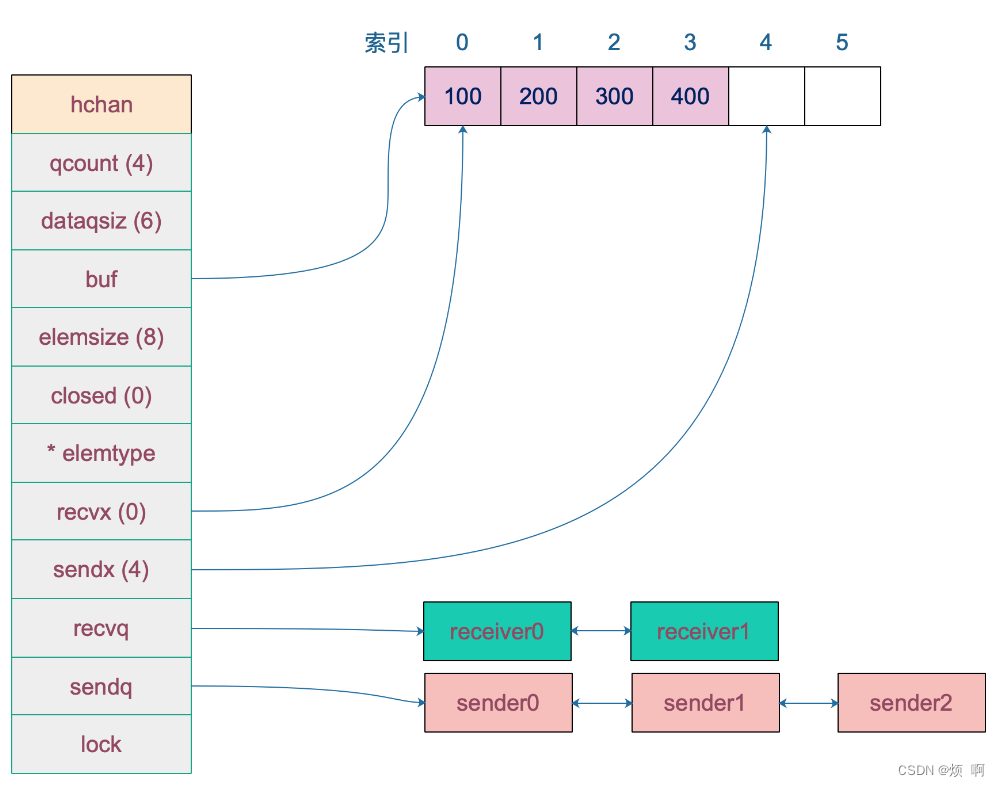
1.概念

插值查找是一种改良版的二分查找,其优势在于,对于较为均匀分布的有序数列,能够更快地使得mid中间游标快速接近目标值.

2.计算公式

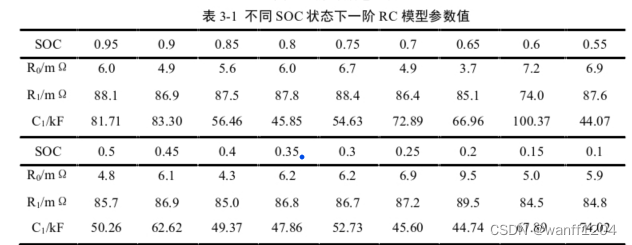
中间游标计算公式.

$mid=low+\frac{(high-low)}{(arr[high]-arr[low])}*(target-arr[low])$

公式说明:

公式的主要思路是,以第一次定位mid中间游标为例, 在接近平均分配的情况下,左右游标之间的差值表示总计供查询的区间有几个元素, 而分母最右游标指示的值减去最左边游标的值,代表的是整个供查找范围的值空间.

最后根据比例大概猜测接近target期望值的游标范围.

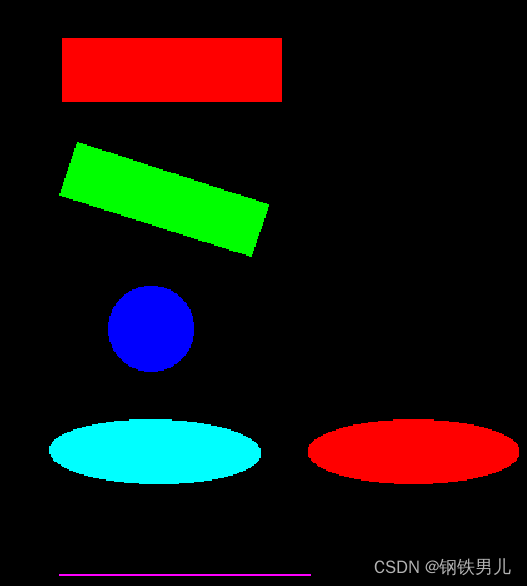
结合下图举例,

在等份的情况下,下标0~7共计8个元素,占值空间为14(16-2), 当查找目标值为4,举例起始点2只有2的差值, 按照等比的办法,目标值4应该在数组前1/4左右的位置.

1.当二分查找时,第一次找到的mid游标为3, 需要找3次mid游标定位才可以找到期望值4的下标为1；

2.当插值查找时,第一次定位mid游标就是1,优势很明显.

3.代码实现

直接基于二分查找中的迭代法替换mid游标计算公式即可.(算法还是以默认升序有序的数组为例)

public int interplatorSearch(int[] arr, int target) {
        //检查数组的有效性
        if (null == arr || arr.length < 1) {
            return -1;
        }

        int low = 0;
        final int length = arr.length;
        int high = length - 1;

        // 先判断头尾游标的值
        if (length == 1) {

            if (arr[0] == target) {
                return 0;
            } else {
                return -1;// not found
            }
        } else { // length >= 2
            if (arr[low] == target) {
                return low;
            } else if (arr[high] == target) {
                return high;
            } else if (arr[low] > target || arr[high] < target) {
                //如果待查找的数值在有序数组最大或者最小值之外,直接判查询未果,无须再插值查找了.
                return -1;
            }
        }

        int mid;
        while (low < high) {
            // 注意分母不能为空
            int valueGap = arr[high] - arr[low];
            if (valueGap <= 0) {
                return -1;// not found
            }

            mid = low + (high - low) * (target - arr[low]) / valueGap;
            System.out.println("low:" + low
                    + ",high:" + high
                    + ",mid:" + mid
                    + ",value[low]:" + arr[low]
                    + ",value[high]:" + arr[high]
                    + ",value[mid]:" + arr[mid]);
            //这段非常重要,否则将可能出现死循环,
            //当头游标和尾游标的中间值已经是起始或者末尾两个游标位之一时,代表查找结束,且无果.
            if (high == mid || low == mid) {
                return -1;
            }
            if (arr[mid] < target) {
                low = mid;
            } else if (arr[mid] > target) {
                high = mid;
            } else if (arr[mid] == target) {
                return mid;
            }
        }
        return -1;
    }