作者:非妃是公主
专栏:《算法》《刷题笔记》
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
《算法》专栏系列文章
算法设计与分析复习01:主方法求递归算法时间复杂度
算法设计与分析复习02:分而治之算法
算法设计与分析复习03:动态规划算法
算法设计与分析复习04:贪心算法算法设计与分析复习05:回溯及分支限界
算法设计与分析复习06:随机化算法
算法设计与分析复习07:样题
文章目录
- 《算法》专栏系列文章
- 题目:攒青豆
- 分析
- 源码
- 存在问题
- 正确思路
- 算法思路
- 数据结构
- 正确源码
题目:攒青豆
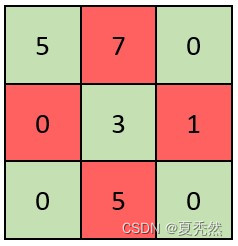
现有 n 个宽度为 1 的柱子,给出 n 个非负整数依次表示柱子的高度,排列后如下图所示,此时均匀从上空向下撒青豆,计算按此排列的柱子能接住多少青豆。(不考虑边角堆积)

以下为上图例子的解析:
输入:height = [5,0,2,1,4,0,1,0,3]
输出:17
解析:上面是由数组 [5,0,2,1,4,0,1,0,3] 表示的柱子高度,在这种情况下,可以接 17 个单位的青豆。
分析
这道题是一道动态规划的题目,和leetcode经典题目接雨水本质是一样的。
结题的思路也是采用动态规划的思想,分为以下几种情况:
- 从前往后遍历数组;
- 如果当前高度高于上一个柱子高度,证明当前柱子的加入,可以继续加入豆子,导致最优解发生了变化,所以要更新前面柱子的高度。
- 这时候,再一次进行遍历;
- 寻找前面比当前柱子高的的柱子(可以把青豆挡住),找到后,更新寻找过程中遇到的柱子的高度较矮的柱子。
- 如果一直找到了初始位置,也没有找到,则说明当前柱子是前面所有柱子中最高的的。这时候说明当前填充高度,为最高的柱子,取开始和当前位置的较低点。
- 如果当前高度低于两边的高度,那么当前填充高度为左、右两个柱子中较短的高度。
源码
# include<iostream>
# include<vector>
using namespace std;
int main() {
vector<int> hight, curHight;
hight = { 5, 2, 7, 4, 9 };
curHight = hight;
for (int i = 1; i < hight.size(); i++) {
if (hight[i] < hight[i - 1] && i + 1 < hight.size() && hight[i] < hight[i + 1]) {
curHight[i] = min(hight[i - 1], hight[i + 1]);
}
else if (hight[i] > hight[i - 1]) {
int j;
for (j = i - 1; j >= 0; j--) {
if (hight[i] <= hight[j]) {
break;
}
}
if (j == -1)j = 0;
int newHight = min(hight[i], hight[j]);
for (int k = j + 1; k < i; k++) {
curHight[k] = newHight;
}
}
}
int sum = 0;
for (int i = 0; i < hight.size(); i++) {
sum += curHight[i] - hight[i];
}
cout << sum;
}
存在问题
但是,注意上面标红的位置,这里是存在问题的!具体是什么问题呢?这种情况下求到的最低点不一定对于前面所有位置都是最低的。具体来看如下例子:
输入:[ 5, 2, 7, 4, 9]
分析:遍历到9的时候,由于9是最大的,因此会一直遍历到初始位置5,这时候程序认为从头到后最高的高度都是5,但是,比如倒数第二个位置,这里的填充高度应该是7,不是5,因此,就出现了错误。
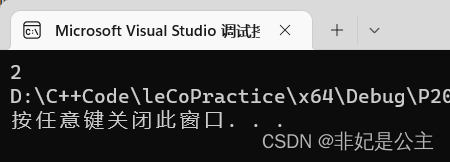
输出:由于程序认为最后填充后的高度都是5,所以所以做差后求解结果为2。
运行程序进行输出验证,结果如下:
正确思路
算法思路
正确思路十分简洁明了:
- 对于每一个位置,记录他左边最高的墙,记录他右边最高的墙。
- 二者取较小的就是能装的最高高度。
- 这两个数组的初始化通过两次遍历实现。(动态规划记录的过程,记录当前最大的)
- 最后求解的时候,遍历一遍实际的柱子,填充到左右两边较低柱子的高度。
数据结构
用两个数组来记录两边的墙,一个记录左边的墙,另一个记录右边的墙。
用1个数组来记录真实的柱子高度。
正确源码
int main() {
vector<int> hight; // 每个位置墙的高度
// 测试用例1
hight = { 5,0,2,1,4,0,1,0,3 };
// 测试用例2
// hight = { 5, 2, 7, 4, 9 };
// 当前位置两边最高的墙的高度
vector<int> leftWall = vector<int>(hight.size(), 0); // 左边最高墙
vector<int> rightWall = vector<int>(hight.size(), 0);// 右边最高墙
// 初始化左边墙的高度
int curMaxHight = hight[0];
for (int i = 0; i < hight.size(); i++) {
curMaxHight = max(curMaxHight, hight[i]);
leftWall[i] = curMaxHight;
}
// 初始化右边墙的高度
curMaxHight = hight[hight.size() - 1];
for (int i = hight.size() - 1; i >= 0; i--) {
curMaxHight = max(curMaxHight, hight[i]);
rightWall[i] = curMaxHight;
}
// 得到当前位置可以填充的高度
int sum = 0;
for (int i = 0; i < hight.size(); i++) {
int canFillHight = min(leftWall[i], rightWall[i]);
sum += canFillHight - hight[i];
}
cout<<sum;
}
在测试用例1下,输出如下:
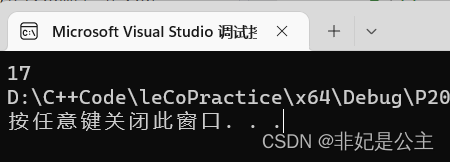
测试用例2下,输出如下: