判断矩阵是否是一个 X 矩阵

难度：简单

如果一个正方形矩阵满足下述 全部 条件，则称之为一个 X 矩阵 ：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0
给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：

输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

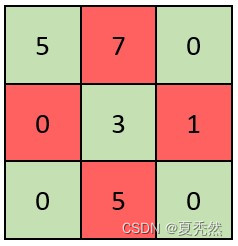
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

模拟

思路：

首先题目给出 $\text{X}$ 矩阵的定义，一个正方形矩阵如果同时满足以下两个条件则该矩阵为 $\text{X}$ 矩阵。

• 矩阵对角线上的所有元素都不是 $0$。
• 矩阵中的所有其他元素都是 $0$。

现在给出一个大小为 $n\times n$ 的二维整数数组 $\text{grid}$，现在我们需要判断 $\text{grid}$ 是否是一个 $\text{X}$ 矩阵。对于矩阵 $\text{grid}$ 中的某一个位置 $(i,j)$，$0\le i,j<n$，如果满足 $i=j$ 或者 $i+j+1=n$，则说明该点在矩阵 $\text{grid}$ 的对角线上，否则不在矩阵对角线上。那么我们遍历矩阵中的每一个位置来判断是否满足 $X$ 的定义即可——若在对角线上则需要满足 $\text{grid}[i][j]\ne 0$，否则需要满足 $\text{grid}[i][j]=0$。如果每一个位置都满足要求则返回 $\text{true}$，否则返回 $\text{false}$。

复杂度分析：

• 时间复杂度： $O(n^2)$，其中 $n$ 为正方形矩阵 $\text{grid}$ 的行列数。
• 空间复杂度： $O(1)$。仅使用常量空间。

class Solution:
    def checkXMatrix(self, grid: List[List[int]]) -> bool:
        length = len(grid)
        for i in range(length):
            for j in range(length):
                if j == i or j == length - 1 - i:
                    if grid[i][j] == 0:
                        return False
                elif grid[i][j]:
                    return False
        return True

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/check-if-matrix-is-x-matrix