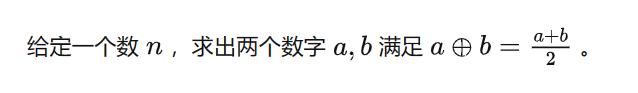2019国赛轨道炮

题目描述

小明在玩一款战争游戏。地图上一共有 N 个敌方单位，可以看作 2D 平面上的点。其中第 i 个单位在 0 时刻的位置是 (Xi​,Yi​)，方向是 Di​ (上下左右之一, 用'U'/'D'/'L'/'R' 表示)，速度是 Vi​。

小明的武器是轨道炮，只能使用一次，不过杀伤力巨大。小明可以选择在某个非负整数时刻释放轨道炮，轨道炮一次可以消灭在一条直线 (平行于坐标轴)上的所有敌方单位。

请你计算小明最多能消灭多少敌方单位。

输入描述

输入第一行包含一个整数 N。

以下 N 行每行包含 3 个整数 Xi​,Yi​,Vi​，以及一个大写字符 Di​。

其中，1≤N≤1000，−10^6≤Xi​,Yi​≤10^6，0≤Vi​≤10^6。

输出描述

输出一个整数代表答案。

输入输出样例

输入

4
0 0 1 R
0 10 1 R
10 10 2 D
2 3 2 L

输出

3

题目大意：

平面上有N个点分别向上，下，左，右四个方向移动，每个点有速度v求解最多会有几个点会在同一行或同一列上（即纵坐标或横坐标相同)

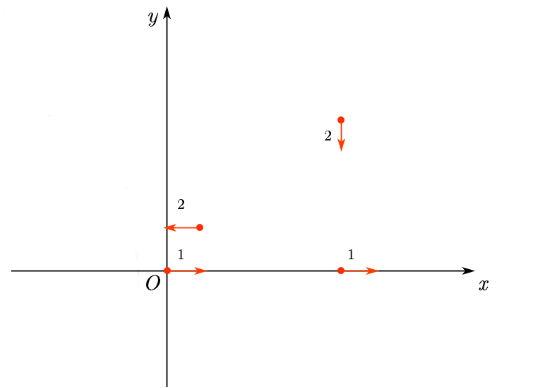
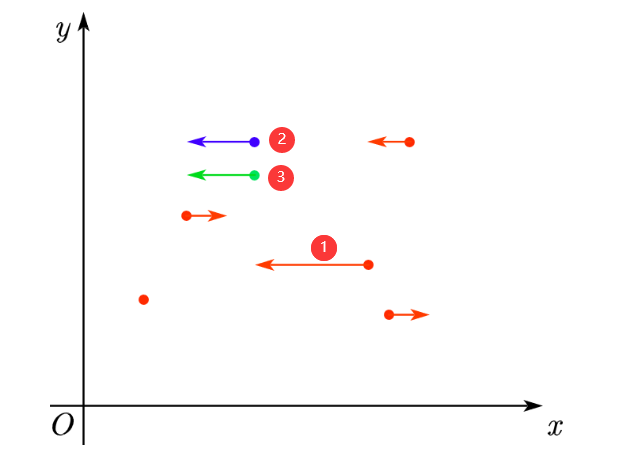
题目样例图示如下，x轴上的两个点永远在同一行上，向下走的点在某一时刻也会到达x轴，这样最多有3个点在同一直线上。
 

每一个点有横纵坐标，速度,运动方向，这些信息如何存储?

创建两个列表存储每个点的横坐标和纵坐标（也可以创建一个列表，每个子列表存储每个点的坐标） ，两个列表存储每个点在横方向的速度和在纵方向的速度

X:[ ]        存储每个点的横坐标
Y:[ ]        存储每个点的纵坐标
vx:[ ]       存储每个点在横方向的速度(没有则为0)
vy:[ ]       存储每个点在纵方向的速度(没有则为0)

速度需要规定方向

• 设定x方向向右为正，向左为负
• 设定y方向向上为正，向下为负

难点︰如何求解最多会有几个点横/纵坐标相同

依次锁定每个点，看看在所有时刻中，它最多会和几个点横/纵坐标相同
依次计算锁定每个点后，取最大值即为最终结果

举例：有4个点
锁定1号:2个

锁定2号:1个

锁定3号:2个

锁定4号:3个

答案:3

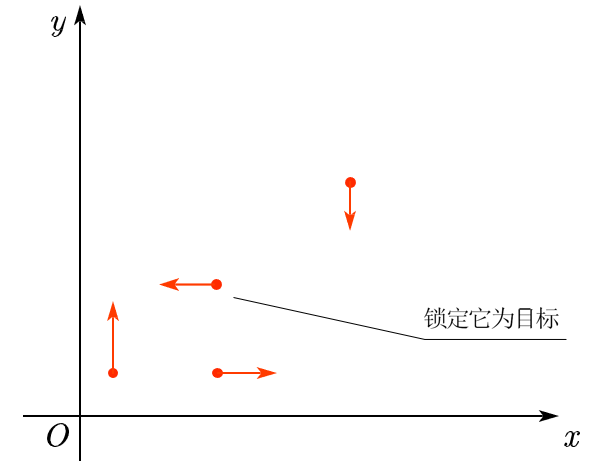
锁定了一个点，如何计算最多的横/纵坐标相同点数?

做法：遍历其他所有点，首先判断它们是否会在某一时刻处于同一行/列
如果会，利用速度差和距离差，计算出同x/y的时刻t（例如下图①和②）

1、计算横坐标时，判断的是横坐标相同情况(同列) 

t=相对距离//相对速度(余数为0是才可能同x/y)

• 相反方向：

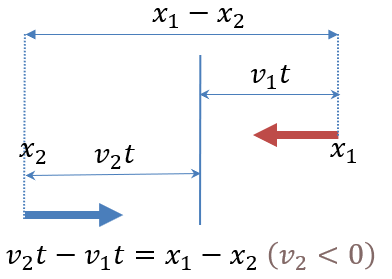
• 相同方向： 

  

还有一部分点，永远和锁定的点处于同行/列。（例如下图②和③）这个要另外处理，因为分母。

2、计算纵坐标时，判断的是纵坐标相同情况(同行)

同上面计算横坐标的方法。

如何记录某一时刻t对应的同x/y的点数?

• 用一个字典d记录每个点和锁定点同心/y的时刻t（字典d的键），然后d[t]+=1(默认空时是0)，即可记录时刻t同x/y的点数（字典的值）
• 有一部分点因为始终与锁定点同x/y，因此另外用一个变量always记录(不存在字典中，因为计算t时分母不能是0)计算一个坐标方向时，定义一个记录最大点数的变量mx，每个锁定点计算完时，从字典中获取最大的值+always，更新最大值。
• 贪心思想：我们锁定每一个点，求它最多会和几个点共线，然后再找所有点的同x/y时刻t的点数的最大值。
• 时间复杂度：
• 最后对横纵坐标分别计算，取二者较大值，即为结果。

 代码:

n =int(input())
N = 1010
X = [0] * N; Y = [0] * N
vx = [0] * N; vy = [0] * N
for i in range(n):
    w = input().split()  # 每一点的x和y
    cx = int(w[0]); cy = int(w[1])
    X[i] = cx; Y[i] = cy 
    v = int(w[2])        # 每一点的速度
    # 四个方向
    if w[3] == 'U':
        vy[i] = v
    elif w[3] == 'D':
        vy[i] = -v
    elif w[3] == 'R':
        vx[i] = v
    elif w[3] == 'L':
        vx[i] = -v

def cal(P, v):
    mx = 0
    for i in range(n):
        d = {}              # 存储同x/y时刻t的点数
        aimx = P[i]; aimv = v[i]
        always = 1          # 始终与锁定点同x/y，锁定点本身就是一个，所以初始化为always = 1，
        for j in range(n):
            if i == j: continue     # 排除和自己的情况
            dx = aimx - P[j]        # 相对位置dx
            dv = v[j] - aimv        # 相对速度dv
            if dv == 0:             # 如果相对速度为0
                if dx == 0:         # 如果是始终与锁定点同x/y
                    always += 1
                mx = max(mx, always) # 更新时刻t的最大值
            else:                   # 相对速度不为0
                t = dx // dv        # 求出同x/y时刻t
                if dx % dv or t < 0:# 排除余数不为0或者时刻t＜0
                    continue
                d[t] = d.get(t, 0) + 1          # 同x/y时刻t的点数+1
                mx = max(mx, d[t] + always)     # 更新时刻t的最大值
    return mx

res = max(cal(X, vx), cal(Y, vy))   # 取同x/y时刻t的点数的最大值就是结果
print(res)