采用M语言对算例进行仿真！！

设置控制对象传递函数：

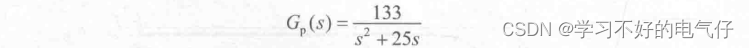
取采样时间为1ms，采用Z变换将对象离散化，并描述为离散状态方程的形式：

x(k +1)= Ax(k)+ B(u(k)+wk))

y(k)= Cx(k)

带有测量噪声的被控对象输出为：

yv(k)=Cx(k)+ v(k)

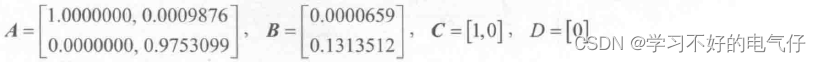
控制干扰信号w(k)和测量噪声信号v(k)幅值均为0.10的白噪声信号，输入信号幅值为1.0、频率为1.5Hz的正弦信号。采用卡尔曼滤波器实现信号的滤波，取Q=1，R=1。仿真时间为3s，原始信号及带有噪声的原始信号、原始信号及滤波后的信号和误差协方差的变化分别如图1~ 3所示。仿真结果表明，该滤波器对控制干扰和测量噪声具有很好的滤波作用。

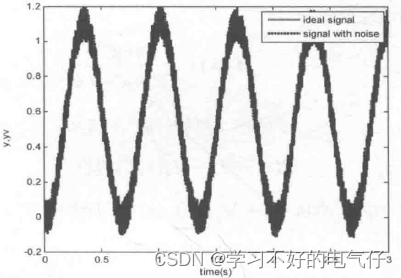
图1 原始信号及带有噪声的原始信号

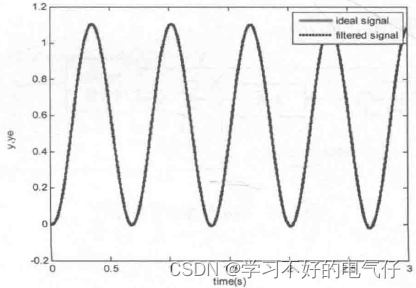
图2 原始信号及滤波后的信号

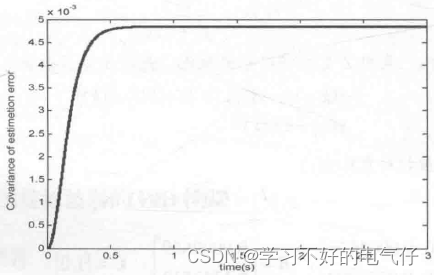
图3 误差协方差的变化

仿真程序：

%Kalman filter

%x=Ax+B(u+w(k));

%y-Cx+D+v(k)

clear all;

close all;

ts=0.001;

M=3000;

%Continuous Plant

a=25;b=133;

sys=tf(b,[1,a,0D);

dsys=c2d(sys,ts,z);

[num.den]=tfdata(dsys,'v');

A1=[0 1;0 -a];

B1=[0;b];

C1=[1 0];

D1=[0];

[A,B，C,D]=c2dm(A1,B1.CI,D1,ts,'zZ);

Q=1; %Covariances of w

R=1; %Covariances of v

P=B*Q*B'; %Initial error covariance

x=zeros(2,1); %Initial condition on the state

ye=zeros(M,1);

ycov=zeros(M,1);

u_1=0;u_2=0;

y_1=0;y_2=0;

for k=1:1;M

time(k)=k*ts;

w(k)=0.10*rands( 1); %Process noise on u

v(k)=0.10*rands(1); %Mcasurement noise on y

u(k)=1.0*sin(2*pi*1.5*k*ts);

u(k)=u(k)+w(k);

y(k)=-den(2)*y_1-den(3)*y_2+num(2)*u1+num(3)*u_2;yv(k)-y(k)+v(k);

%Measurement update

Mn=P*C(C*P*C'+R);P=A*P*A+B*Q*B';P=(eye(2)-Mn*C)*P;

x=A*x+Mn*(yv(k)-C*A*x);

ye(k)-C*x+D; %Filtered value

errcov(k)-C*P*C; %Covariance ofestimation error

%Time update

x=A*x+B*u(k);

u_2=u_1;u_1=u(k);y_2=y_1:y 1=ye(k);

end

figure(1);

plot(time,y,'r, time,yv,k:','linewidth’,2);

xlabel('time(s));ylabel('y.yv')

legend(ideal signal','signal with noise');

figure(2);

plot(time,y,'r,time,ye,'k:' linewidth',2);

xlabel( 'time(s)':ylabel('y, ye')

legend(ideal signal','filtered signal');

figure(3);

plot(time,errcov 'k'. Tinewidth' 2);

xlabel( 'time(s)';ylabel('Covariance of estimation error');