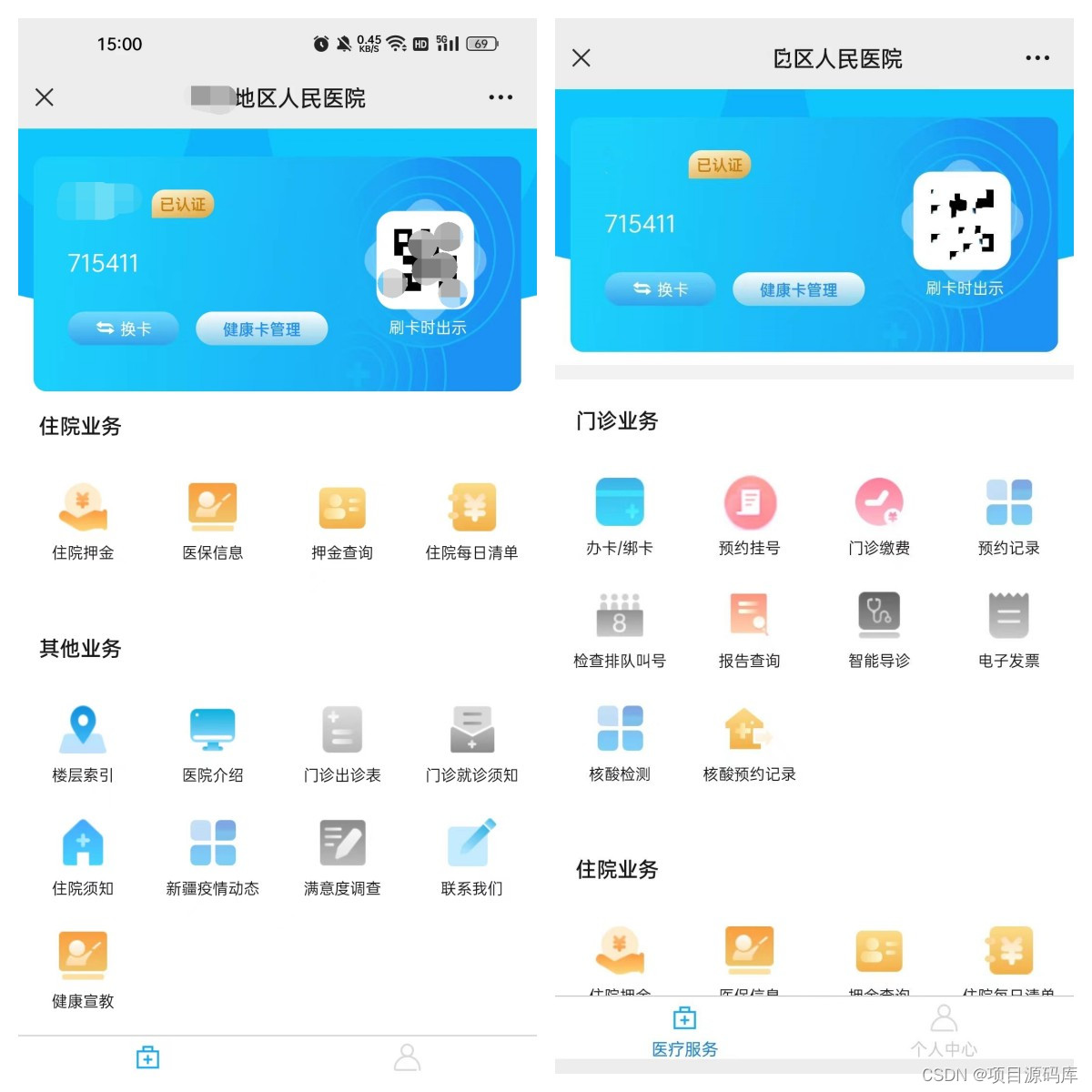
- 含义
- 首先:对评价目标进行多层次矛盾分解
- 其次:利用突变理论和模糊数学相结合产生突变模糊隶属函数
- 再次:由归一公式进行综合量化运算
- 最终:归一为一个参数,即求出总的隶属函数,从而对评价目标进行排序分析
- 特点
- 不对指标采用权重,但考虑各评价指标的相对重要性
- 减少主观性又不失科学合理性,计算简易准确,应用范围广
- 步骤
- 对评价总指标进行多层次分解
- 排列成倒立树状目标层次结构
- 原始数据只需知道最下层子指标的数据即可
- 各指标的分解一般不超过4个
- 确定突变评价指标体系的突变系统类型
- 常见突变系统类型
- 尖点突变系统
- 特点:一个指标仅分解成两个子指标
- 模型:f(x)=x[4]+ax[2]+bx
- 燕尾突变系统
- 特点:一个指标可分解为三个子指标
- 模型:f(x)=((1/5)x[5])+((1/3)ax[3])+((1/2)bx[2])+cx
- 蝴蝶突变系统
- 特点:一个指标能分解为四个子指标
- 模型:f(x)=((1/6)x[6])+((1/4)ax[4])+((1/3)bx[3]) +((1/2)cx[2])+dx
- f(x)表示一个系统的一个状态变量x的势函数,系数a、b、c、d表示该状态变量的控制变量
- 尖点突变系统
- 常见突变系统类型
- 由突变系统的分叉方程导出归一公式
- 尖点突变系统:
- x[,a]=a[1/2],xb=b[1/3]
- 燕尾突变系统:
- x[,a]=a[1/2],x[,b]=b[1/3],x[,c] =c[1/4]
- 蝴蝶突变系统:
- x[,a]=a[1/2],x[,b]=b[1/3],x[,c]=c[1/4],x[,d]=d[1/5]
- 式中x[,a]表示对应a的x值,x[,b]表示对应b的x值。
- 尖点突变系统:
- 利用归一公式进行综合评价
- 根据多目标模糊决策理论,对同一方案,在多种目标情况下,如设A[,1],A[,2],……,A[,m]为模糊目标,则理想的策略为: C=A[,1]IA[,2]I……A[,m],其隶属函数为:μ(x)=μ[,A1](x)∧μ[,A2](x)∧……μ[,Am](x),式中μ[, A](x)μA[,1](x)为A[,1]的隶属函数,定义为此方案的隶属函数,即为各目标隶属函数的最小值。
- 对于不同的方案,如设G[,1],G[,2],……,G[,n],记G[,i]的隶属函数为u(G[,i]),则表示方案G[,i]优于方案G[,j]。因而利用归一公式对同一对象各个控制变量(即指标)计算出的对应的X值应采用“大中取小”原则,但对存在互补性的指标,通常用其平均数代替,在对象的最后比较时要用“小中取大”原则,即对评价对象按总评价指标的得分大小排序。由此可以看出,对各级指标指数的确定,实际上是对其下一级指标指数(或数值)进行综合排序的结果。
- 对评价总指标进行多层次分解