风控图算法之中心性算法(小数据集Python版)
图算法在金融风控领域的应用已经超越了传统的社区发现技术,这些技术曾被主要用于识别和分析欺诈性行为模式,例如黑产团伙。当前,一系列图统计算法,包括介数中心性(Betweenness)、核(Kcore)、以及PageRank等,正逐渐展现出它们在风险评估和管理中的重要作用。这些算法不仅作为辅助判别工具,帮助揭示交易网络中的潜在风险点,而且在识别网络中的核心和影响力节点方面发挥着关键作用。通过精确识别这些核心节点,金融机构能够更有效地监测和防范可能的风险传播路径,从而增强整体的风险控制框架。
文章目录
- 风控图算法之中心性算法(小数据集Python版)
- 一、Betweenness(介数中心性)
- 二、PageRank
- 三、Degree Centrality(度中心性)
- 四、Closeness Centrality(接近中心性)
- 五、K-core Centrality(K-core中心性)
- 总结
一、Betweenness(介数中心性)
在图算法中,Betweenness(介数中心性)是一个用于衡量节点在图中的中心性或重要性的指标。它反映了一个节点在图中作为最短路径中介的频率。以下是介数中心性算法的原理:
-
最短路径:介数中心性基于图中所有最短路径的概念。对于任意两个节点对(u, v),如果它们的最短路径经过了节点i,则节点i对这对节点对的介数有贡献。
-
介数计算:对于每个节点i,算法计算通过该节点的最短路径数量与所有可能的节点对的最短路径数量的比例,这个比例即为节点i的介数中心性。
-
公式表达:对于节点i的介数中心性(CB_i),其计算公式可以表示为:
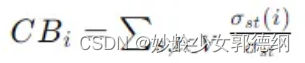
-
算法步骤:
- 计算图中所有节点对的最短路径。
- 对于每个节点,累加它在所有节点对的最短路径中的出现次数。
- 将每个节点的累加值除以所有节点对的数量,得到最终的介数中心性。
-
应用:介数中心性可以用于识别网络中的关键节点,例如社交网络中的影响力者或金融交易网络中的潜在风险传播点。
-
局限性:介数中心性算法的一个局限性是计算复杂度较高,尤其是对于大型图,因为它需要计算所有节点对之间的最短路径。
-
优化:为了解决这个问题,研究者们提出了一些近似算法或启发式算法,如Brandes的算法,它利用动态规划的思想来提高介数中心性的计算效率。
-
介数中心性算法在网络分析中是一个强大的工具,尤其是在需要识别网络中的关键桥梁或潜在的瓶颈时。在风控领域,它可以帮助识别可能影响网络稳定性的节点,从而采取预防措施。
二、PageRank
PageRank是一个非常经典的用于衡量图中节点重要性的算法。
PageRank原理
注意:Python实现的PageRank支持带权图的计算,但不支持设置各个顶点的初始分值,SparkGraphX实现的PageRank既不支持带权图的计算,又不支持设置各个顶点的初始分值,若要支持,需要二次开发。
三、Degree Centrality(度中心性)
度中心性是指一个节点链接的节点数(即节点的度)。在有向图中,分为入度中心性和出度中心性。度中心性可以直观地反映一个节点的活跃程度或其网络中的影响力。例如,在社交网络中,一个人如果有更多的朋友(更高的度中心性),可能拥有更高的社交地位。
四、Closeness Centrality(接近中心性)
接近中心性(Closeness Centrality)是网络分析中的一个概念,用于衡量一个节点在网络中相对于其他所有节点的中心程度。它反映了一个节点到网络中所有其他节点的平均距离。以下是接近中心性算法的原理:
- 平均距离:接近中心性基于一个节点到网络中所有其他节点的最短路径长度的平均值。这个平均值越小,表示该节点越接近网络的中心。
- 最短路径:对于网络中的任意两个节点,最短路径是连接它们的边数最少的路径。在有向图中,需要考虑边的方向。
注意:对于非连通图一般无法计算接近中心性,如果非要计算,比较常见的做法是,现对其使用弱连通分量算法,然后对每个连通分量再行计算接近中心性。
五、K-core Centrality(K-core中心性)
K-core中心性(K-core Centrality)是图论中用于识别网络中最核心和最紧密连接的节点或子图的一种度量。K-core中心性基于k-core的概念,其中k-core是图中的一个最大子图,其中每个节点至少与k个其他节点相连(在无向图中即为每个节点的度都至少为k)。
K-Core 的计算通常包括以下步骤:
- 从图中删除所有度小于 ( k ) 的节点。
- 删除这些节点后,可能会有更多节点的度变为小于 ( k )。继续删除这些节点。
- 重复步骤2,直到没有更多度小于 ( k ) 的节点为止。
最后剩下的子图就是 ( k )-core。这个过程是迭代的,可能需要多次遍历图中的节点。
注意:K-core计算得到的子图不一定是连通的,但是它的大小一定是大于等于k的。
总结
上述所有涉及到的代码都在风控图算法之中心性算法(小数据集Python版)
如果可以的话,麻烦关注一下啦~~~