【力扣高频题】004.两个正序数组的中位数

news2024/10/6 10:39:59

------------------ 长文警告 ------------------

4.两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 $O (l o g (m + n))$ 。

示例 1：

输入： nums1 = [1,3], nums2 = [2]

输出： 2.00000

解释： 合并数组 = [1,2,3] ，中位数 2 。

示例 2:

输入： nums1 = [1,2], nums2 = [3,4]

输出： 2.50000

解释： 合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5 。

思路分析

本题的暴力思路其实很简单：

由于两个数组是正序的，因此可以采用 双指针 的方式将两个数组合并成为一个新的有序数组，并根据m + n为奇数还是偶数返回其中位数即可
该方法由于使用了双指针的方式，需要遍历整个数组，因此其时间复杂度为 $O (M a x (m, n))$

但由于本题要求时间复杂度为 $O (l o g (m + n))$ ，因此需要探究一种更加高效的算法。

接下来我们先来介绍并实现 两个函数 ，进而对本题进行求解。

函数一：

函数功能： 合并两个有序且长度相等的数组，返回其中位数（奇数长度时）或上中位数（偶数长度时）。因此很显然，需要分两种情况进行讨论。

长度为偶数
- 以数组长度为 4 进行举例说明：

长度为奇数
- 以数组长度为 5 进行举例说明：

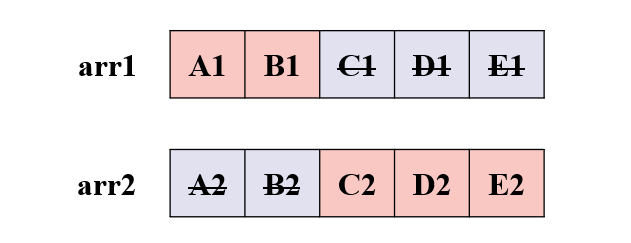
因此，为了能够继续使用该函数进行递归，需要从较长数组中舍弃一个。

舍弃方法是：长数组的最小值与短数组的最大值进行比较。

函数二：

函数功能： 合并两个有序但不一定等长的数组，返回其第 K 小的数。

下面对以上三种不同的情况进行讨论分析，为方便说明，取n = 3和m = 7：

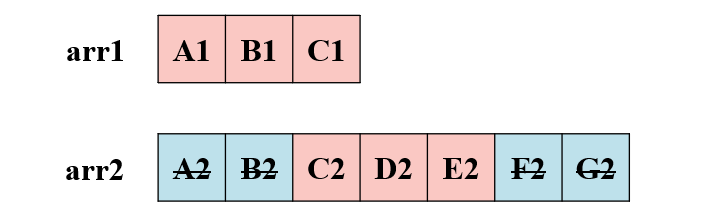
与情况 2）推广与证明方法类似，这里不再赘述，感兴趣的小伙伴可以仿照 2）证明一下该方法的正确性。

至此，我们就介绍完了两个函数的功能：

函数一getUpMedian： 合并两个有序且长度相等的数组，返回其上中位数。

函数二findKthNum： 合并两个有序但不一定等长的数组，返回其第 K 小的数。

实现了这两个函数功能后，本题主函数思路就很容易构思到了：

给定两个任意长度的数组后，

若两数组长度之和为奇数时，调用findKthNum(size/2+1)，求中位数。
若两数组长度之和为偶数时，调用findKthNum(size/2)和findKthNum(size/2+1)，再求二者均值，即中位数。
注意考虑边界条件，若其中一个数组长度为 0 ，直接返回另外一个有序数组的上中位数即可。

函数一代码

public static int getUpMedian(int[] A, int s1, int e1, int[] B, int s2, int e2) {
    int mid1 = 0;
    int mid2 = 0;
    while (s1 < e1) {
        mid1 = (s1 + e1) / 2;
        mid2 = (s2 + e2) / 2;
        if (A[mid1] == B[mid2]) {
            return A[mid1];
        }
        if (((e1 - s1 + 1) & 1) == 1) { // 奇数长度
            if (A[mid1] > B[mid2]) {
                if (B[mid2] >= A[mid1 - 1]) {
                    return B[mid2];
                }
                e1 = mid1 - 1;
                s2 = mid2 + 1;
            } else { // A[mid1] < B[mid2]
                if (A[mid1] >= B[mid2 - 1]) {
                    return A[mid1];
                }
                e2 = mid2 - 1;
                s1 = mid1 + 1;
            }
        } else { // 偶数长度
            if (A[mid1] > B[mid2]) {
                e1 = mid1;
                s2 = mid2 + 1;
            } else {
                e2 = mid2;
                s1 = mid1 + 1;
            }
        }
    }
    return Math.min(A[s1], B[s2]);
}

函数二代码

public static int findKthNum(int[] arr1, int[] arr2, int K) {
    int[] longs = arr1.length >= arr2.length ? arr1 : arr2;
    int[] shorts = arr1.length < arr2.length ? arr1 : arr2;
    int m = longs.length;
    int n = shorts.length;
    if (K <= n) {
        return getUpMedian(shorts, 0, K - 1, longs, 0, K - 1);
    }
    if (K > m) {
        if (shorts[K - m - 1] >= longs[m - 1]) {
            return shorts[K - m - 1];
        }
        if (longs[K - n - 1] >= shorts[n - 1]) {
            return longs[K - n - 1];
        }
        return getUpMedian(shorts, K - m, n - 1, longs, K - n, m - 1);
    }
    if (longs[K - n - 1] >= shorts[n - 1]) {
        return longs[K - n - 1];
    }
    return getUpMedian(shorts, 0, n - 1, longs, K - n, K - 1);
}

主函数

public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n1 = nums1.length;
    int n2 = nums2.length;
    int size = n1 + n2;
    boolean even = (size & 1) == 0;
    if (n1 != 0 && n2 != 0) {
        if (even) {
            return (double) (findKthNum(nums1, nums2, size / 2) + findKthNum(nums1, nums2, size / 2 + 1)) / 2D;
        } else {
            return findKthNum(nums1, nums2, size / 2 + 1);
        }
    } else if (n1 != 0) {
        if (even) {
            return (double) (nums1[(size - 1) / 2] + nums1[size / 2]) / 2;
        } else {
            return nums1[size / 2];
        }
    } else if (n2 != 0) {
        if (even) {
            return (double) (nums2[(size - 1) / 2] + nums2[size / 2]) / 2;
        } else {
            return nums2[size / 2];
        }
    } else {
        return 0;
    }
}