快速幂算法

快速幂算法是一种通过分治和递归的方式来计算幂运算的方法，其核心思想是利用分治和递归减少乘法的次数来显著提高效率。

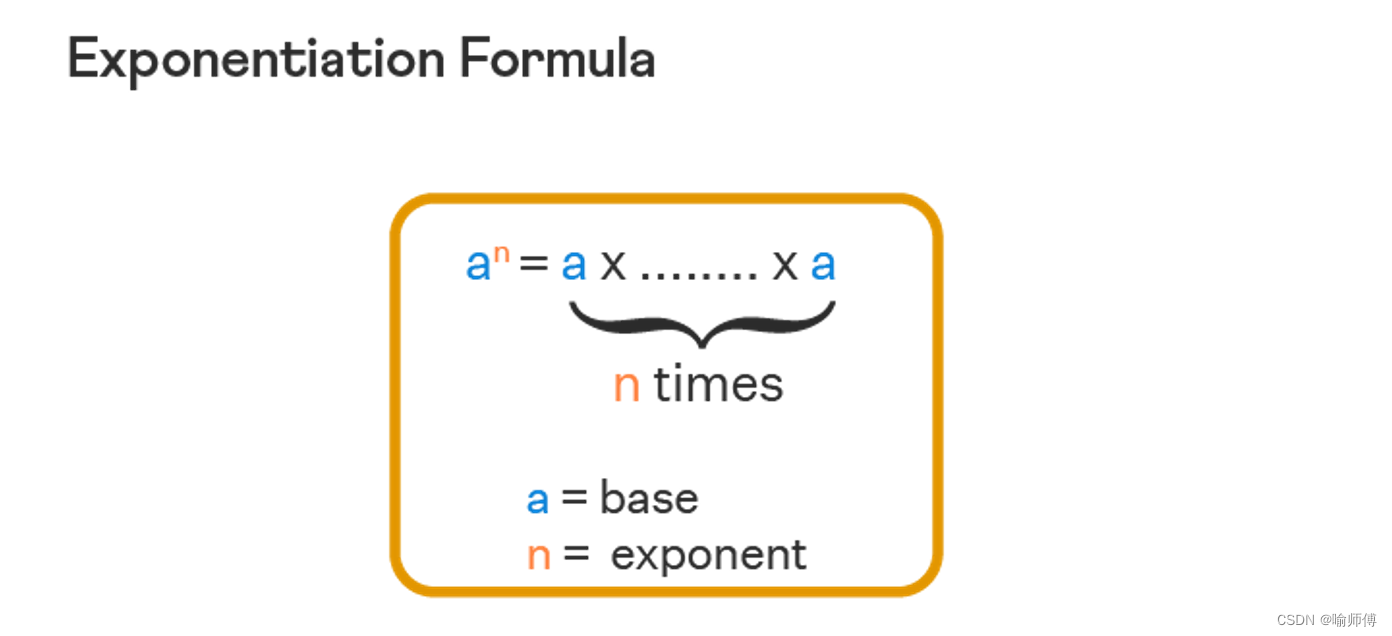
基本原理：

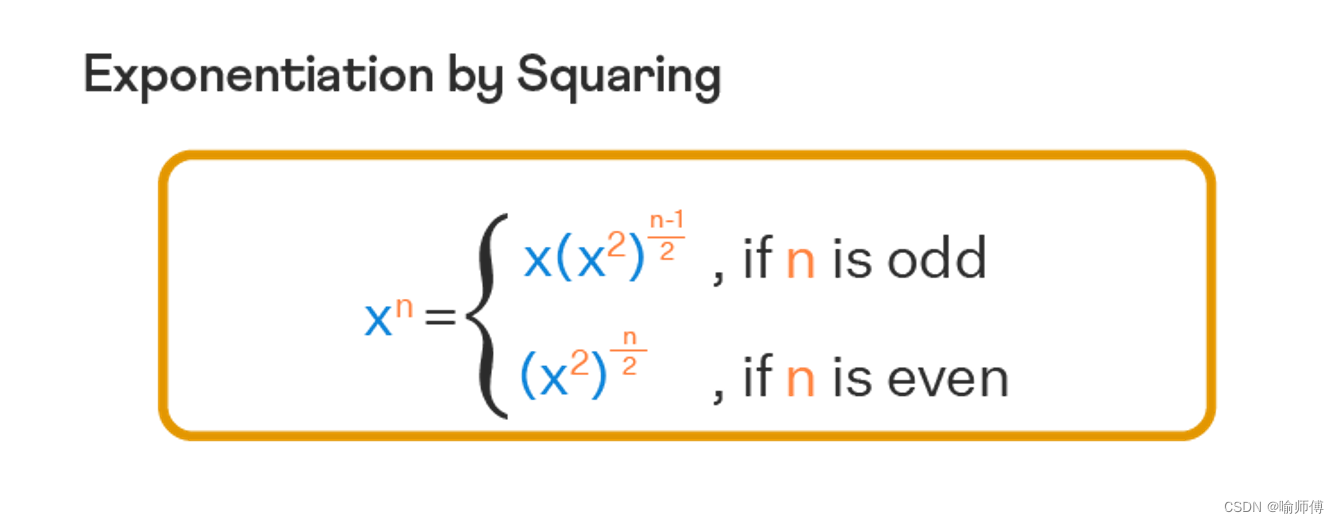
给定 x 和 n，计算 x^n 的过程如下：

• 基本情况处理：如果指数 n 是 0，直接返回 1.0。
• 递归计算：
  • 计算 x^(n/2)，即 half。
  • 如果 n 是偶数，x^n = (x^(n/2))^2 = half * half。
  • 如果 n 是奇数，x^n = x * x^(n-1) = half * half * x。
    通过递归地将指数 n 分解为更小的指数，从而减少了乘法的次数，达到了快速计算幂的效果。

代码实现（Java）：

class Solution {
    // 主函数，计算 x 的 n 次幂
    public double myPow(double x, int n) {
        // 如果 x 是 0 或者 1，直接返回 x
        if (x == 0 || x == 1) return x;
        
        // 如果 n 是负数，返回 x 的 -n 次幂的倒数
        if (n < 0) {
            return 1 / myHelper(x, -n);
        } else { // 如果 n 是非负数，直接调用 myHelper 计算 x 的 n 次幂
            return myHelper(x, n);
        }
    }

    // 辅助函数，使用递归和分治算法计算 x 的 n 次幂
    public double myHelper(double x, int n) {
        // 基本情况：任何数的 0 次幂都是 1
        if (n == 0) return 1;
        
        // 基本情况：任何数的 1 次幂都是它本身
        if (n == 1) return x;
        
        // 递归计算 x 的 n/2 次幂
        double half = myHelper(x, n / 2);
        
        // 如果 n 是偶数，x^n = (x^(n/2))^2
        if ((n & 1) == 0) {
            return half * half;
        } else { // 如果 n 是奇数，x^n = x * (x^(n/2))^2
            return half * half * x;
        }
    }
}

—

利用递归和分治的方法，快速幂算法可以在 O(log n) 的时间复杂度内完成指数运算，比朴素的循环逐步相乘要高效得多。