前言

在windows系统的磁盘管理中误删了ubuntu的磁盘分区，开机后一直卡在grub界面。

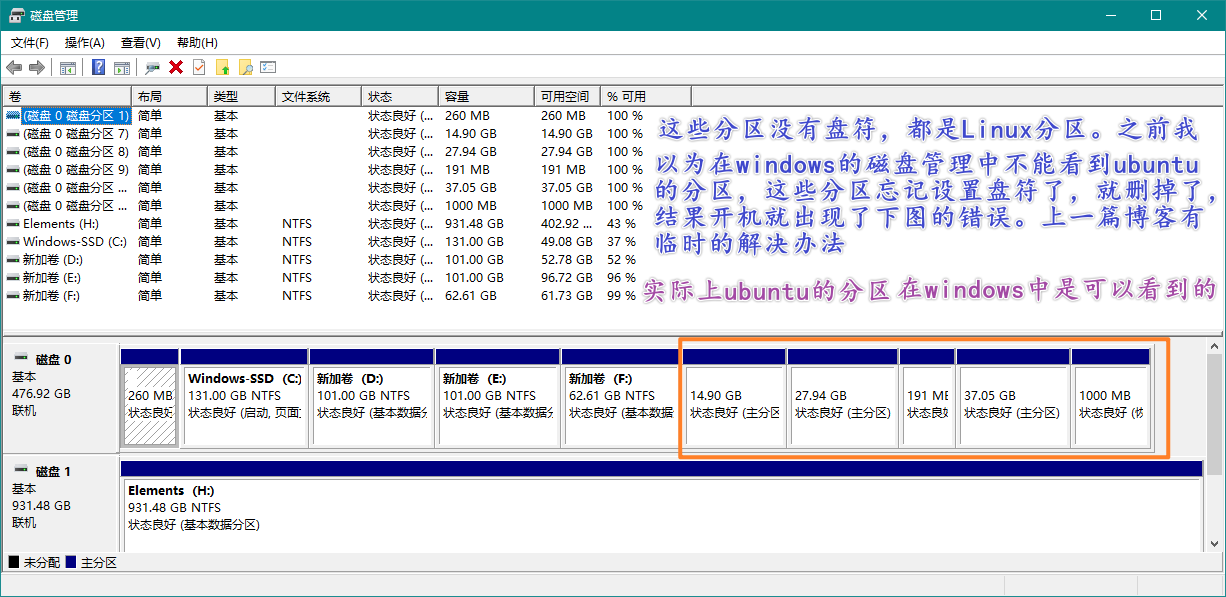
Windows/Linux双启动的机器一般都使用grub作为引导程序。如果不小心在Windows中删除了linux分区，grub就会因为找不到配置文件而造成无法启动。

系统配置  

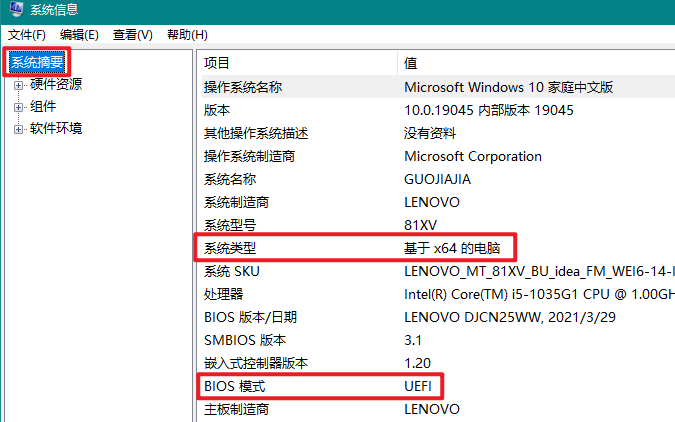
系统类型：基于x64的电脑

磁盘分区形式：GPT（GUID分区表）

BIOS模式(开机引导方式)：UEFI

引导区：/efi

windows分区所属的磁盘序号：0

系统类型和BIOS模式查看方法：win+R组合键->cmd->msinfo32

windows分区所属的磁盘序号查看方法：win+R组合键->diskmgmt.msc打开磁盘分区管理，在所有分区中找到格式为NTFS,备注有 启动 关键词的

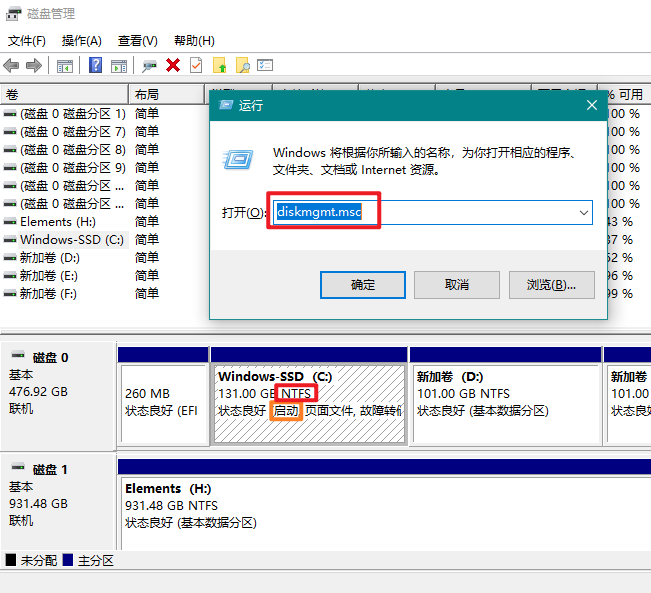
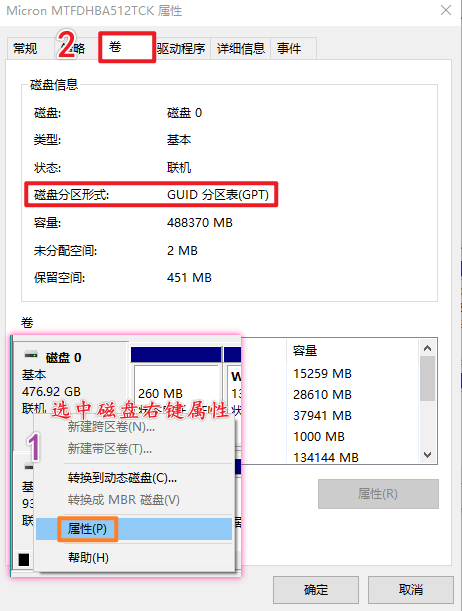
磁盘分区形式查看方法：在磁盘管理中选中磁盘->右键->属性（BIOS模式确定后可以不查看磁盘分区形式，因为Windows系统中GPT和UEFI是强制对应的，win8之后的电脑都是GPT分区的）

恢复win10自己的引导系统

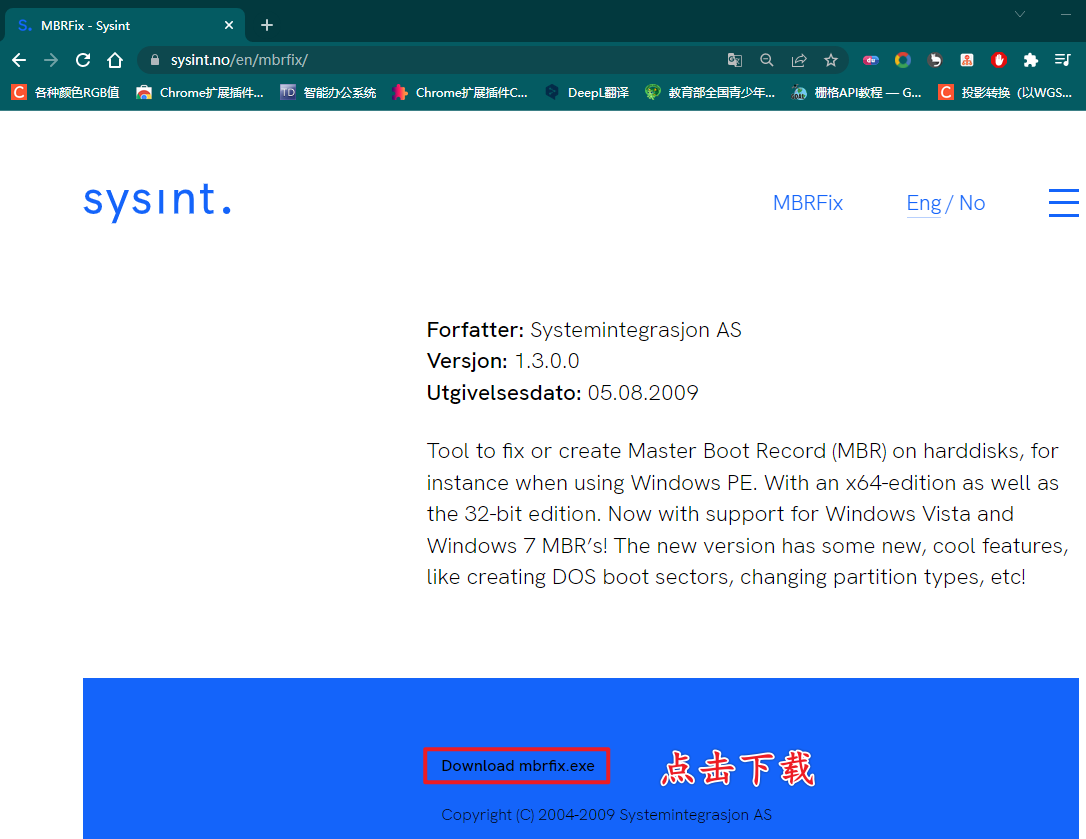
下载一个MBR引导修复工具，进入网站，点击

 会提示下载一个mbrfix压缩包

解压压缩包，将解压后的文件夹复制到C盘根目录下，以便我们在命令行里能快速的找到并运行它们。

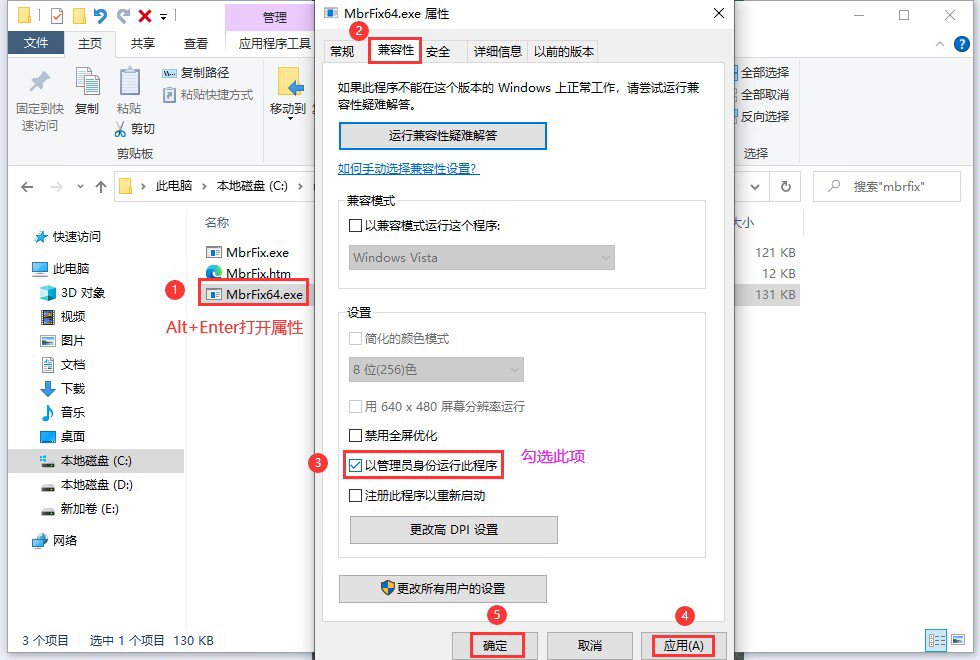
修改.exe文件的权限使其能够对引导区进行修改（修改完成后会看到.exe图标右下角多了一个盾牌标记）

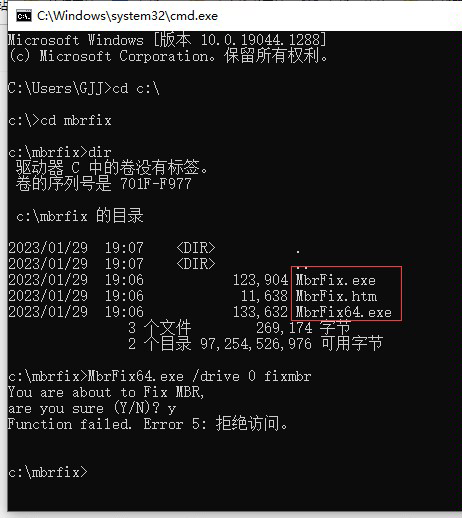
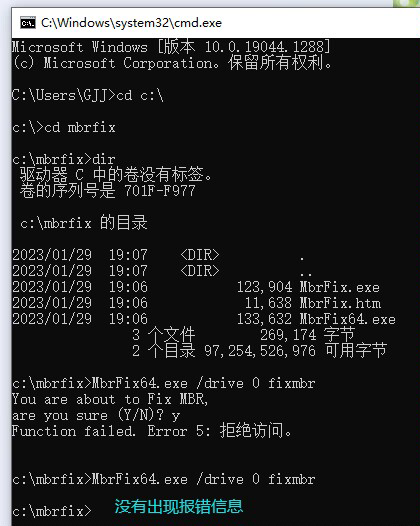
输入指令 MbrFix64. exe /drive 0 fixmbr，输入y

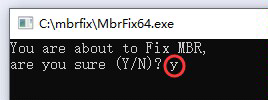
如果没有出现报错信息，说明修复成功了。重启电脑测试一个能够进入windows系统。