算法设计与分析--考试真题

news2024/11/26 14:38:09

  • 分布式算法试题汇总
    • 选择题
    • 简答题
    • 算法题
  • 2013级试题
  • 2019级试题
  • 2021年秋
  • 考卷

根据考试范围找相应题目做。

分布式算法试题汇总

选择题

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

  1. 下述说法错误的是___
    A 异步系统中的消息延迟是不确定的
    B 分布式算法的消息复杂性是指在所有合法的执行上发送消息总数的最大值
    C 在一个异步算法中，如果不存在错误，则算法的执行只取决于初始配置
    D 分布式系统终止是指系统中所有结点处于终止状态，且没有消息在传输

  2. 已知有三个阻碍分布式了解全局状态，与全局状态无关的是 （）
    A. 非及时的通信
    B. 相关性影响
    C. 中断
    D. 算法的正确性

在分布式系统中，有三个主要的阻碍了解全局状态的因素，分别是：

  • 非及时的通信：由于网络延迟，消息的传递可能不是按照发送的顺序到达接收方，导致事件的顺序不一致，从而影响全局状态的判断。
  • 相关性影响：由于分布式系统中的组件之间存在依赖关系，一个组件的状态可能会影响另一个组件的状态，从而影响全局状态的判断。
  • 中断：由于分布式系统中的组件可能会发生故障或恢复，导致系统的可用性和一致性受到影响，从而影响全局状态的判断。

因此，与全局状态无关的是算法的正确性。算法的正确性是指算法能够按照预期的功能和性能执行，不受外部因素的干扰。算法的正确性是分布式系统设计和实现的基础，而不是了解全局状态的障碍。

  1. 设正整数d1,d2,…,dn是n个结点的标识符集合，x = min(d1,d2,…,dn),y =max(d1,d2,…,dn)，则同步环上非均匀的leader选举算法的时间复杂性是
    A. O(n)
    B. O(xn)
    C. (yn)
    D. O(nlogn)

  2. 在异步环上，一个O(n^2)的leader选举算法按顺时针单向发送消息，假设只有最大的标识符节点可以当选为leader,则当环上标识符次序为__时该算法发送的消息数量最多。
    A. 0,1, … , n-1 随机
    B. 逆时针 n-1,n-2,…,0
    C. 顺时序 0,1，…, n-1
    D. 顺时针 n-1,n-2,…,0

简答题

  1. 已知事件 e1,e2,e3 和 e4 的向量时戳分别为（2,3,0,0），（1,2,0,0），（0,0,1,1），（3,6,4,2），请找出所有因果关系的事件对。

（1,2,0,0）<v （2,3,0,0），e2 在因果序上先于 e1
（2,3,0,0）<v （3,6,4,2），e1 在因果序上先于 e4
（1,2,0,0）<v （3,6,4,2），e2 在因果序上先于 e4
（0,0,1,1）<v （3,6,4,2），e3 在因果序上先于 e4

如果事件e1在事件e2之前发生，或者事件e1导致事件e2发生，那么事件e1因果先于事件e2，记为e1 -> e2。向量时戳的一个重要性质是，如果 e 1 < v e 2 e1 <_v e2 e1<v​e2，那么e1的向量时戳的每个元素都小于或等于e2的向量时戳的对应元素。

  1. 分布式算法中，bit复杂性和消息链复杂性分别属于通信复杂性和时间复杂性中的哪一种？

bit 复杂性属于通信复杂性，消息链复杂性属于时间复杂性；若在一个分布式算法中每个 msg信息的 bit 数目相同，则 msg 的个数就等于 bit 的总数除以一个 msg 的 bit 数目，则 bit 复杂性可以等价为 msg 复杂性；消息链复杂性是最长消息链的长度，在同步系统中它就是最大轮数，异步系统中假定任何执行的 msg 延迟至多是一个单位时间，它就是计算直到终止时间的最大运行时间，在同，异步系统中皆为时间复杂性。

  • 通信复杂性可以进一步分为两种：bit复杂性和消息复杂性。bit复杂性是指算法在执行过程中所传输的比特数，它反映了算法的通信量。消息复杂性是指算法在执行过程中所传输的消息数，它反映了算法的通信次数。
  • 时间复杂性也可以进一步分为两种：同步时间复杂性和异步时间复杂性。同步时间复杂性是指算法在同步模型下的执行时间，它反映了算法的同步性能。异步时间复杂性是指算法在异步模型下的执行时间，它反映了算法的异步性能。
    因此，bit复杂性属于通信复杂性中的一种，而消息链复杂性属于时间复杂性中的一种。消息链复杂性是指算法在异步模型下的最长消息链的长度，它反映了算法的最坏情况下的延迟。
    消息复杂性和消息链复杂性的区别：
    消息复杂性和消息链复杂性是两种不同的时间复杂性的指标，它们分别反映了算法在通信次数和延迟方面的性能。
  • 消息复杂性是指算法在执行过程中所传输的消息数，它反映了算法的通信次数。消息复杂性越小，说明算法的通信开销越低。
  • 消息链复杂性是指算法在异步模型下的最长消息链的长度，它反映了算法的延迟。消息链复杂性越小，说明算法的响应时间越快。
  1. 构造一个 16 节点的环，使其高度对称，并给出所有序等价的连续片段。

0 0000 0000 0
1 0001 1000 8
2 0010 0100 4
3 0011 1100 12
4 0100 0010 2
5 0101 1010 10
6 0110 0110 6
7 0111 1110 14
8 1000 0001 1
9 1001 1001 9
10 1010 0101 5
11 1011 1101 13
12 1100 0011 3
13 1101 1011 11
14 1110 0111 7
15 1111 1111 15
长度为 1 的有序等价的连续片段:
(0)，(8), (4), (12), (2), (10), (6), (14), (1), (9), (5), (13), (3), (11), (7), (15)
长度为 2 的有序等价的连续片段:
(0, 8),(4, 12),(2, 10),(6, 14),(1, 9), (5, 13), (3, 11), (7, 15);
(8, 4), (12, 2), (10, 6), (14, 1), (9, 5), (13, 3), (11, 0)
长度为 4 的有序等价的连续片段：
0, 8, 4, 12 || 2, 10, 6, 14 || 1, 9, 5, 13 || 3, 11, 7, 15;
15 0, 8, 4 || 12, 2, 10, 6 || 14, 1, 9, 5 || 13, 3, 11, 7;
7, 15 0, 8, || 4, 12, 2, 10, || 6, 14 1, 9, || 5, 13 3, 11;
11, 7, 15 0, || 8, 4, 12, 2, || 10, 6, 14, 1, || 9, 5, 13 3;
长度为 8 的有序等价的连续片段:
0, 8, 4, 12 2, 10, 6, 14 || 1, 9, 5, 13 || 3, 11, 7, 15;
15 0, 8, 4 12, 2, 10, 6 || 14, 1, 9, 5 , 13, 3, 11, 7;
7, 15 0, 8, 4, 12, 2, 10, || 6, 14 1, 9, 5, 13 3, 11;
11, 7, 15 0, 8, 4, 12, 2, || 10, 6, 14, 1, 9, 5, 13, 3;
3, 11, 7, 15 0, 8, 4, 12, || 2 10, 6, 14, 1, 9, 5, 13 ;
13, 3 11, 7, 15 0, 8, 4, || 12, 2 10, 6, 14, 1, 9, 5;
5, 13, 3 11, 7, 15 0, 8, || 4 12, 2 10, 6, 14, 1, 9 ;
9, 5, 13, 3 11, 7, 15 0, || 8, 4 12, 2 10, 6, 14, 1;
长度为 16 的有序等价的连续片段(0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15）

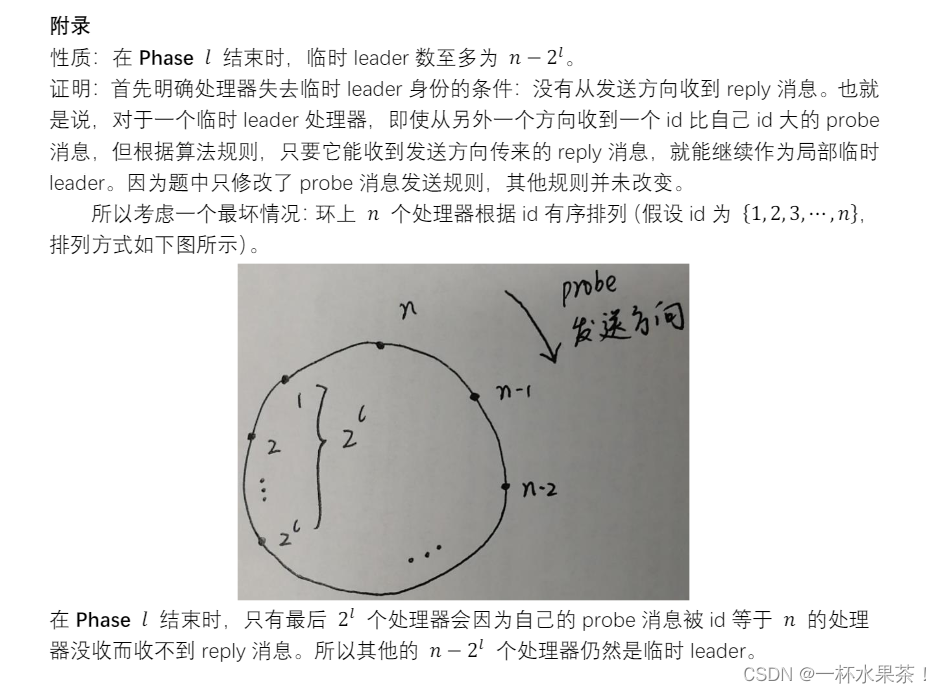
  1. 若将消息复杂度为 O(nlgn)的异步环选举算法（在阶段 1 向节点的 2 邻居发送 Prob 消息）修改为只向其中一个方向发送 Prob 消息，请问修改后算法的消息复杂度是多少？如何对其做进一步的修改使得消息复杂度仍然为 O(nlgn)。

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

算法题

在这里插入图片描述
在这里插入图片描述

设一个同步匿名的单向环有 n 个结点，每个结点均知道 n，每个节点的初始均状态相同，
每个结点上的程序相同且开始于同一时刻。
（1） 请问是否存在一个确定的算法选出一个 leader？简述理由。
（2） 试设计一个概率的 leader 选举算法。
（3） 请问你设计的概率算法属于哪一类算法？

（1） 对于同步环上的 leader 选举， 不存在非均匀的匿名算法。

  • 初始状态相同：在一个匿名环中，处理器间始终保持对称，若无某种初始的非对称(如，
    标识符唯一)， 则不可能打破对称。 在匿名环算法里， 所有处理器开始于相同状态。
  • 在同步系统中， 一个算法以轮的形式进行，根据引理 3.1 在环 R 上算法 A 的容许执行
    里， 对于每一轮 k，所有处理器的状态在第 k 轮结束时是相同的。
    由反证法，假设若在某轮结束时， 一个处理器宣布自己是 leader(进入选中状态)， 则其它处理器亦同样如此， 这和 A 是一个 leader 选举算法的假定矛盾！

（2）算法由若干个 phase 构成，每个 phase 包括 n 轮，可用 phase 和轮控制算法流程。每
个结点可以设置一个随机数发生器 uniform(1…m),这里 m 是局部变量，初值等于 n。
每个结点上的随机数发生器 uniform(1…m)产生随机数𝑥𝑖当作自己的 id
在第 i 阶段开始

  1. 若一个结点的 id 是 i，则该结点绕环发送一个包含信息 i 的 msg；
  2. 若一结点的 id 不是 i， 且它收到一个 msg， 则它转发此 msg 后变为 non-leader，变成
    non-leader 之后能转发 msg。
  3. 若一个结点的 id 是 i， 同时收到一个 msg，则本地变量 count 记录收到了多少个 msg。
    id 为 i 的结点收到了 msg 数量,代表当前系统中产生了最小 id 的结点个数。此时 id 为 i 的结
    点把 Phase 变为 1，m 变成 count。重新执行以上过程，直到 id 为 i 的结点只收到一个 msg,
    此时该结点为 leader,同时绕环发送终止 msg,收到终止 msg 的 non-leader 终止运行。

（3）Las Vegas 算法。因为自己提出的算法一定能获得正确的解，但是随机算法可能会以极低的概率一直产生相同𝑥𝑖，导致不能产生最终解。

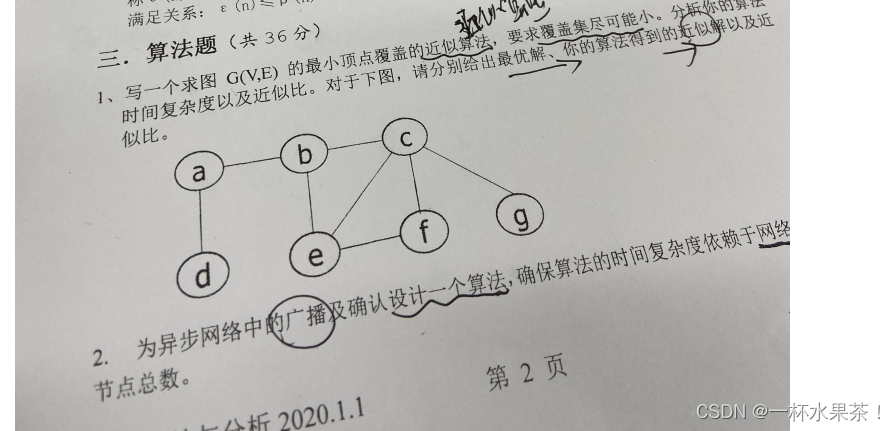
在这里插入图片描述

在这里插入图片描述

5.分布式系统中生成树构造问题：构造一棵具有 m 条边（信道总数），网络直径为 D 的生成
树，其构造方法是将 flooding 算法修改后得到的
（1）若设系统中处理器个数为 n，那么最坏情况下，异步算法完成生成树构造需要发送的
消息数是多少？
（2）基于异步算法找到该网络的一课生成树的时间复杂性、消息复杂性分别是多少？
（3）若在同步模型下进行生成树构造，其与异步算法的区别是什么？它构造的是 BFS 还是
DFS？请证明你的结果。

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2013级试题

在这里插入图片描述
在这里插入图片描述

2019级试题

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2021年秋

在这里插入图片描述

考卷

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1873158.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【实用指南】铝聚合物电容器的焊接技巧与故障排除，工程师必备知识

【实用指南】铝聚合物电容器的焊接技巧与故障排除，工程师必备知识

铝聚合物电容器是一种电解电容器&#xff0c;在电子元器件领域&#xff0c;以其卓越的性能表现逐渐成为工程师们青睐的选择&#xff0c;尤其在对电容特性有严格要求的应用场合。其特点是使用铝箔作为阳极&#xff0c;并在阳极表面形成一层氧化铝&#xff08;Al2O3&#xff09;作…
阅读更多...
国产固态光耦在工业照明领域的应用

国产固态光耦在工业照明领域的应用

工业照明作为工厂和生产设施中不可或缺的一部分&#xff0c;其效率和安全性直接影响到生产运行的顺畅性和员工的工作环境。国产固态光耦作为现代工业照明技术的重要组成部分&#xff0c;在提升照明系统效率和安全性方面发挥着关键作用。本文将深入探讨国产固态光耦在工业照明领…
阅读更多...
高效实现虚拟机（VMware）安装教程（附安装包）

高效实现虚拟机（VMware）安装教程（附安装包）

目录 一.下载VMware Wworkstation Pro 二 安装&#xff1a; 注&#xff1a;若是安装完VMware&#xff0c;还想在上面安装Centos、Ubuntu&#xff0c;系统请转到基于VMware的linux操作系统安装&#xff08;附安装包&#xff09;-CSDN博客 一.下载VMware Wworkstation Pro 渠道…
阅读更多...
leetCode.92. 反转链表 II

leetCode.92. 反转链表 II

leetCode.92. 反转链表 II 题目思路 代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode …
阅读更多...
【Python数据分析与可视化】：使用【Matplotlib】实现销售数据的全面分析 ——【Matplotlib】数模学习

【Python数据分析与可视化】：使用【Matplotlib】实现销售数据的全面分析 ——【Matplotlib】数模学习

目录 安装Matplotlib 1.打开PyCharm&#xff1a; 2.打开终端&#xff1a; 3.安装Matplotlib&#xff1a; 4.确认安装&#xff1a; 导入Matplotlib 创建简单的折线图 代码解析&#xff1a; 创建子图 代码解析&#xff1a; 创建柱状图 代码解析&#xff1a; 创建散点…
阅读更多...
初识DDD

初识DDD

DDD领域驱动设计 1 DDD是什么&#xff1f; 领域驱动设计&#xff08;Domain-Driven Design, DDD&#xff09;是一种软件设计方法论&#xff0c;旨在处理复杂的业务需求和系统设计。由Eric Evans在他的同名书中提出&#xff0c;DDD关注将业务需求和软件架构紧密结合&#xff0…
阅读更多...
算法设计与分析--近似算法作业及答案

算法设计与分析--近似算法作业及答案

近似算法作业题目 1 k-center 近似算法题目描述参考答案解答 题目 2 均衡负载算法题目描述参考答案解答 题目 3 多项式归约题目描述参考答案解答 近似算法–徐小华 近似算法作业 题目 1 k-center 近似算法 题目描述 问题 1&#xff1a;假设给定 n n n 个指定的城市在一个平…
阅读更多...
findfont: Generic family ‘sans-serif‘ not found because none of the ...: SimHei

findfont: Generic family ‘sans-serif‘ not found because none of the ...: SimHei

警告过程 python代码在使用matplotlib画图时&#xff0c;如果在title&#xff0c;xlabel&#xff0c;ylabel中出现了中文&#xff0c;则会出现字体警告&#xff0c;中文字符显示为方框 例如代码&#xff1a; # matplotlib画图# 设置色带plt.imshow(data, cmapplt.cm.YlGn) #…
阅读更多...
Python基于逻辑回归分类模型、决策树分类模型、随机森林分类模型和XGBoost分类模型实现乳腺癌分类预测项目实战

Python基于逻辑回归分类模型、决策树分类模型、随机森林分类模型和XGBoost分类模型实现乳腺癌分类预测项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 在当今医疗健康领域&#xff0c;乳腺癌作为威胁女性健康的主要恶性肿瘤之一&#xff0c;其早期诊断与精…
阅读更多...
仓库管理系统16--入库管理

仓库管理系统16--入库管理

原创不易&#xff0c;打字不易&#xff0c;截图不易&#xff0c;多多点赞&#xff0c;送人玫瑰&#xff0c;留有余香&#xff0c;财务自由明日实现。 1、创建物资入库用户控件 <UserControl x:Class"West.StoreMgr.View.InStoreView"xmlns"http://schema…
阅读更多...
市场拓展招聘：完整指南

市场拓展招聘：完整指南

扩大招聘业务会给你带来很多挑战&#xff0c;更不用说你已经在处理的问题了。助教专业人士每周花近13个小时为一个角色寻找候选人。此外&#xff0c;客户的需求也在不断变化&#xff0c;招聘机构之间的竞争也在加剧。毫无疑问&#xff0c;对增长有战略的方法会有很大的帮助。一…
阅读更多...
RocketMq源码解析九：刷盘机制及过期文件删除

RocketMq源码解析九：刷盘机制及过期文件删除

一、刷盘机制 刷盘策略在不同时间进行刷写磁盘。RocketMQ的存储是基于JDK NIO的内存映射机制(MappedByteBuffer)的，消息存储首先将消息追加到内存，再根据配置的刷写磁盘 同步刷盘表示消息追加到内存后，立即将数据刷写到文件系统中。代码的调用链如下： submi…
阅读更多...
web使用cordova打包Andriod

web使用cordova打包Andriod

一.安装Gradel 1.下载地址 Gradle Distributions 2.配置环境 3.测试是否安装成功 在cmd gradle -v 二.创建vite项目 npm init vitelatest npm install vite build 三.创建cordova项目 1.全局安装cordova npm install -g cordova 2. 创建项目 cordova create cordova-app c…
阅读更多...
学习过程中遇到的 部分问题及解决办法

学习过程中遇到的 部分问题及解决办法

1.安装build wheel时报错&#xff1a; The detected CUDA version (12.1) mismatches the version that was used to compile PyTorch (11.7). Please make sure to use the same CUDA versions. 由于cuda版本和 当前虚拟环境中的pytorch-cudatoolkit版本不同&#xff0c; 解…
阅读更多...
梦想CAD二次开发

梦想CAD二次开发

1.mxdraw简介 mxdraw是一个HTML5 Canvas JavaScript框架&#xff0c;它在THREE.js的基础上扩展开发&#xff0c;为用户提供了一套在前端绘图更为方便&#xff0c;快捷&#xff0c;高效率的解决方案&#xff0c;mxdraw的实质为一个前端二维绘图平台。你可以使用mxdraw在画布上绘…
阅读更多...
【系统架构设计师】五、计算机网络(概念|通信技术|网络技术)

【系统架构设计师】五、计算机网络(概念|通信技术|网络技术)

目录 一、计算机网络概念 二、通信技术 三、网络技术 3.1 局域网(LAN) 3.1.1 局域网拓扑结构 3.1.2 局域网协议 3.2 无线局域网(WLAN) 3.3 广域网(WAN) 3.4 城域网&#xff08;MAN) 3.5 移动通信网 四、组网技术 4.1 OSI七层模型 4.1.1 交换机 4.1.2 路由器 4.2…
阅读更多...
idea Error running ‘Application‘

idea Error running ‘Application‘

1、Error running ‘Application’ Error running ApplicationError running Application. Command line is too long.Shorten the command line via JAR manifest or via a classpath file and rerun.找到 .idea/libraies/workspace.xml 中的 PropertiesComponent 属性&#…
阅读更多...
python数据分析与可视化二

python数据分析与可视化二

公共部分 # 引入数据分析工具 Pandas import pandas as pd # 引入数据可视化工具 Matplotlib import matplotlib.pyplot as plt # 引入科学计算库numpy import numpy as np from scipy import stats #解决输出时列名对齐问题 pd.set_option(display.unicode.east_asian_wid…
阅读更多...
《数据结构与算法基础 by王卓老师》学习笔记——2.2线性表的案例引入

《数据结构与算法基础 by王卓老师》学习笔记——2.2线性表的案例引入

案例一&#xff1a;一元多项式的运算 案例二&#xff1a;稀疏多项式的运算 案例三&#xff1a;图书信息管理系统 总结
阅读更多...
慢动作视频怎么制作？5种方法，轻松制作慢动作视频

慢动作视频怎么制作？5种方法，轻松制作慢动作视频

在短视频风靡的当下&#xff0c;慢动作视频凭借其独特的视觉效果和引人入胜的节奏感&#xff0c;成为了吸引观众眼球的利器。你是否也想知道如何制作这种令人心动的慢动作视频呢&#xff1f;下面教大家5种能够制作出慢动作视频的方法&#xff0c;一起来学习下吧。 方法一&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023