数据结构_优先级队列(堆)

news2024/9/17 8:28:22

一、优先级队列

1.1 堆

1.2 PriorityQueue接口

二、模拟实现优先级队列

2.1 初始化

2.2 创建大根堆 (向下调整)

2.3 堆的插入

2.4 堆的删除

2.5 堆排序

总结

一、优先级队列

优先级队列是一种特殊的队列，其出队顺序与入队顺序无关，而与优先级相关。其常见的实现方式就是使用堆作为底层数据结构。

1.1 堆

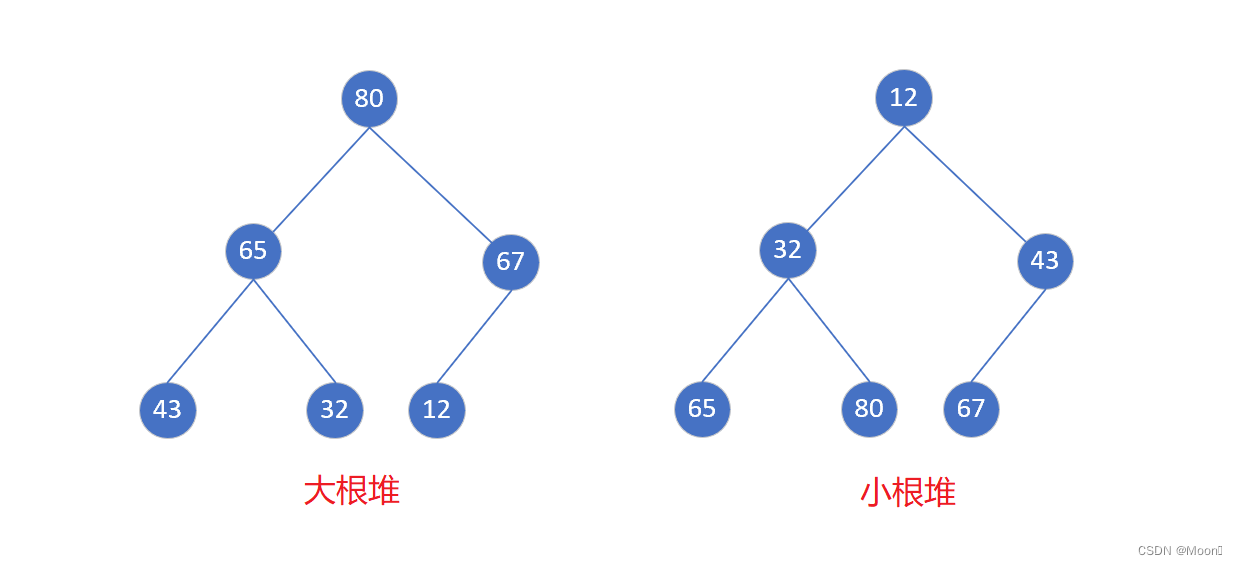
堆将所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，堆还分为大根堆和小根堆。

大根堆：每个结点的值都大于其子结点的值，最大值总是在堆顶。

小根堆：每个结点的值都小于其子结点的值，最小值总是在堆顶。

【完全二叉树的性质】

一棵有 n 个结点的完全二叉树，对于其编号为 i 的结点有：

若 i > 0，父结点编号：[(i-1) / 2]；若 i = 0，则 i 为根结点编号，无父结点。
若 2i+1 < n，左孩子编号：2i+1；反之无左孩子。
若 2i+2 < n，右孩子编号：2i+2；反之无右孩子。

1.2 PriorityQueue接口

在 Java 中提供了 PriorityQueue 和 PriorityBlockingQueue 接口来表示优先级队列，其中 PriorityQueue 线程不安全的，PriorityBlockingQueue 是线程安全的。

【PriorityQueue 的性质】

PriorityQueue 中放置的元素必须能够比较大小，否则会抛 ClassCastException。
不能插入 null 对象，否则会抛 NullPointerException。
没有容量限制，可以任意插入元素，其内部会自动扩容。
插入和删除元素的时间复杂度为 $O(log_{2}N)$ 。
PriorityQueue 底层使用了堆数据结构，默认情况下是小根堆。

【构造方法】

方法	说明
PriorityQueue()	创建一个空的优先级队列，默认容量是11
PriorityQueue(int initialCapacity)	创建一个初始容量为 initialCapacity (不能小于1) 的优先级队列
PriorityQueue(Collection<? extends E> c)	用一个集合来创建优先级队列

【操作方法】

方法	说明
boolean offer(E e)	插入元素 e
E poll()	移除优先级最高的元素并返回
E peek()	获取优先级最高的元素
int size()	获取优先级队列中有效元素个数
boolean isEmpty()	判断优先级队列是否为空
void clear()	清空

二、模拟实现优先级队列

2.1 初始化

public class MyHeap {
    public int[] element;//定义数组以实现优先级队列(堆)
    public int usedSize;//记录堆中有效元素个数
    
    public MyHeap() {
        this.element = new int[10];
    }

    //初始化 element 数组
    public void initElement(int[] array) {
        for (int i = 0; i < array.length; i++) {
            //存入元素
            element[i] = array[i];
            //记录元素个数
            usedSize++;
        }
    }
}

2.2 创建大根堆 (向下调整)

① 初始令 parent 引用指向最后一棵子树的根结点进行调整，调整完一棵子树后，令 parent-- 前往其上一棵子树进行调整，直至调整完下标为 0 的根结点及其子树。

② 首先确保该根结点有左孩子的情况下，进入向下调整的过程，先令 child 引用指向孩子结点最大值；

再比较 parent 与 child 大小，若 child 比 parent 大，则交换，交换后 parent 引用指向当前 child 引用，child 引用指向 parent 左孩子结点开始调整其下方子树，直至其下方不存在子树；

反之无需交换，直接结束循环。

    //创建大根堆：采用向下调整策略
    public void createHeap() {
        //从最后一棵子树开始调整，依次往前，直至根结点
        //父亲结点 = (孩子结点-1) / 2
        //usedSize-1 是树中最后一个结点
        for (int parent = (usedSize-1-1) / 2; parent >= 0; parent--) {
            //向下调整
            siftDown(parent,usedSize);
        }
    }

    //向下调整
    private void siftDown(int parent, int length) {
        //左孩子结点 = 父亲结点*2 + 1
        int child = parent*2 + 1;

        //首先保证该结点有左孩子结点
        while (child < length) {

            //确定该结点有右孩子结点，再进行比较
            //保证 child 引用指向孩子结点中最大值
            if ((child+1) < length && element[child] < element[child+1]) {
                //若右孩子的值大于左孩子，则 child 引用指向右孩子
                child = child + 1;
            }

            if (element[child] > element[parent]) {
                //若 child 比 parent 大，则交换元素
                swap(child, parent);

                //parent 指向 child 位置，向下调整至下方无子树
                parent = child;
                child = parent*2 + 1;
            } else {
                //子结点都比父结点小
                break;
            }
        }
    }

    //交换元素
    private void swap(int i, int j) {
        int tmp = element[i];
        element[i] = element[j];
        element[j] = tmp;
    }

2.3 堆的插入

① 将 value 存放至最后一个结点，开始向上调整。

② 在向上调整的过程中，只需比较 value 与当前的父亲结点大小，若需要交换，交换后 child 指向 parent，parent 指向 child 父结点；反之调整结束。

    //入堆
    public void offer(int value) {
        if (isFull()) {
            element = Arrays.copyOf(element, 2*element.length);
        }
        //将 value 放至最后一个结点
        element[usedSize] = value;
        //向上调整
        siftUp(usedSize);

        usedSize++;
    }

    private boolean isFull() {
        return usedSize == element.length;
    }

    //向上调整
    public void siftUp(int child) {
        //value 的父亲结点
        int parent = (child-1) / 2;

        //调整至 child 指向下标为 0 的根结点
        while (child > 0) {
            //比较两者大小
            if (element[child] > element[parent]) {
                swap(child, parent);
                //交换后，child 指向 parent，parent 指向 child 父结点
                child = parent;
                parent = (child-1) / 2;
            } else {
                break;
            }
        }
    }

2.4 堆的删除

核心：将堆顶结点与最后一个结点交换，usedSize-- 实现出堆操作，最后向下调整为大根堆。

    //出堆
    public int poll() {
        //判空
        if (isEmpty()) {
            throw new EmptyException("堆为空！");
        }
        //记录堆顶元素
        int old = element[0];
        //堆顶结点与最后一个结点交换
        swap(0, usedSize-1);
        //删除原堆顶元素
        usedSize--;
        //出堆后开始向下调整为大根堆
        siftDown(0, usedSize);
        //返回堆顶元素
        return old;
    }

    private boolean isEmpty() {
        return usedSize == 0;
    }

2.5 堆排序

① 创建大根堆，初始化 end = userSzie-1，即 end 指向最后一个结点；

② 将栈顶元素交换至 end 下标。由于大根堆中栈顶元素最大，故交换一次，end--，保证每次交换后的栈顶元素位置不变；

③ 重新向下调整为大根堆；

④ 重复 ②、③ 操作，直至排序完成。

    //堆排序
    public void heapSort() {
        int end = usedSize-1;
        while (end > 0) {
            //将大根堆中栈顶元素交换至 end
            swap(0, end);
            //向下调整为大根堆
            siftDown(0, end);
            //保证每次调整的栈顶元素位置不变
            end--;
        }
    }