📢博客主页：https://blog.csdn.net/2301_779549673
📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！
📢本文由 JohnKi 原创，首发于 CSDN🙉
📢未来很长，值得我们全力奔赴更美好的生活✨

---

📢前言

• 上一篇博客中详细介绍了六大常用排序
• 包括选择、插入、冒泡、希尔、快速、堆排序
• 这次再扩充一个计数排序
• 并简述一下基数排序和桶排序

---

🏳️‍🌈计数排序

我们先来看一下计数排序的$gif$图，简单理解一下

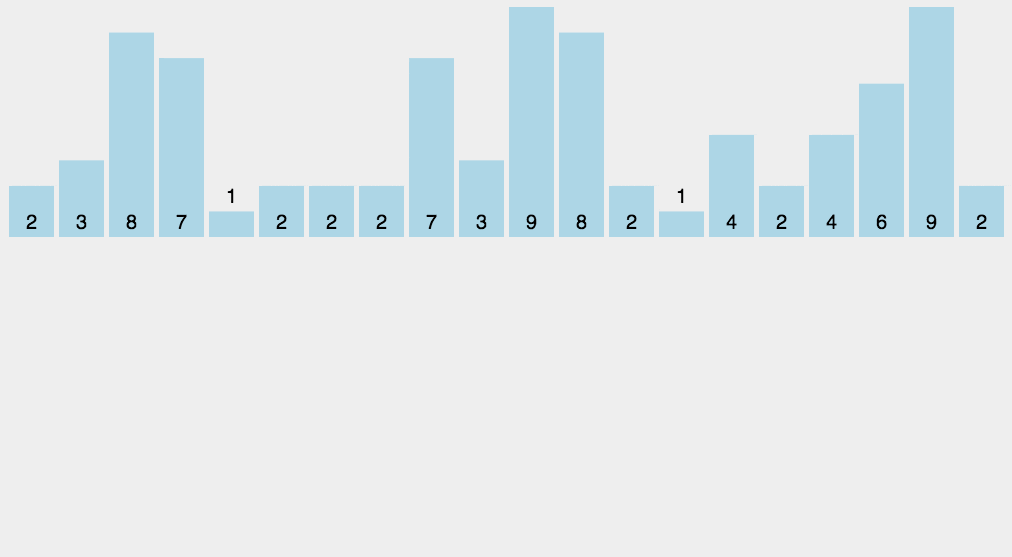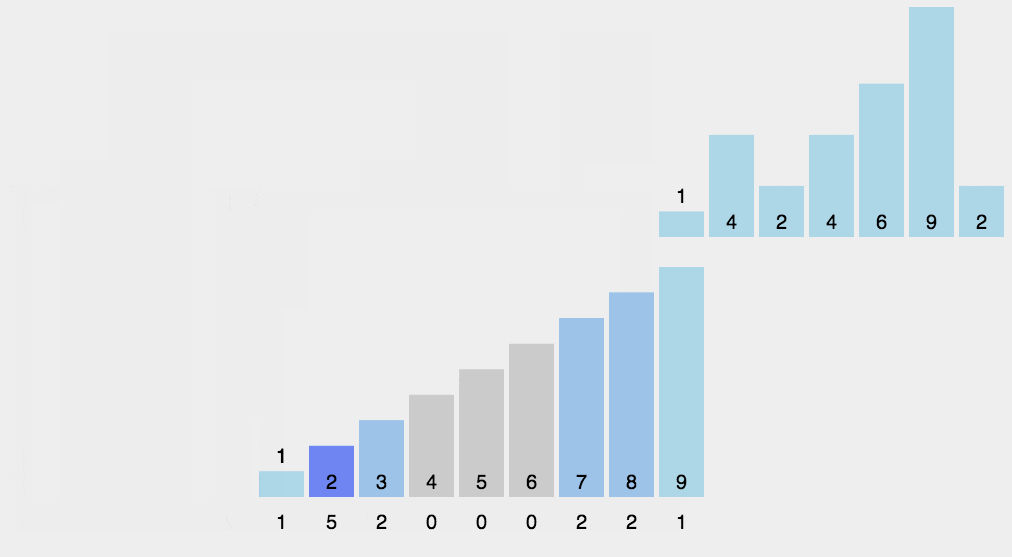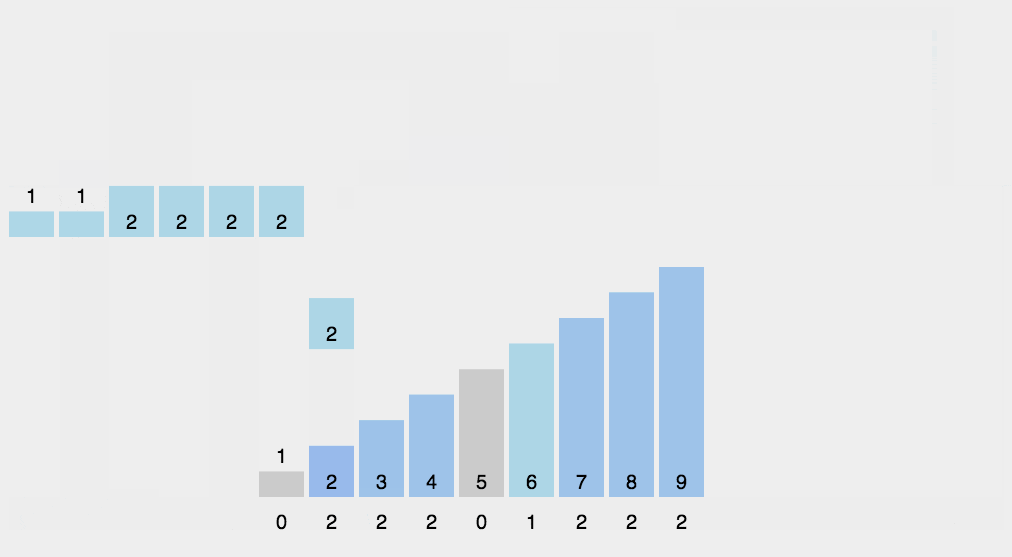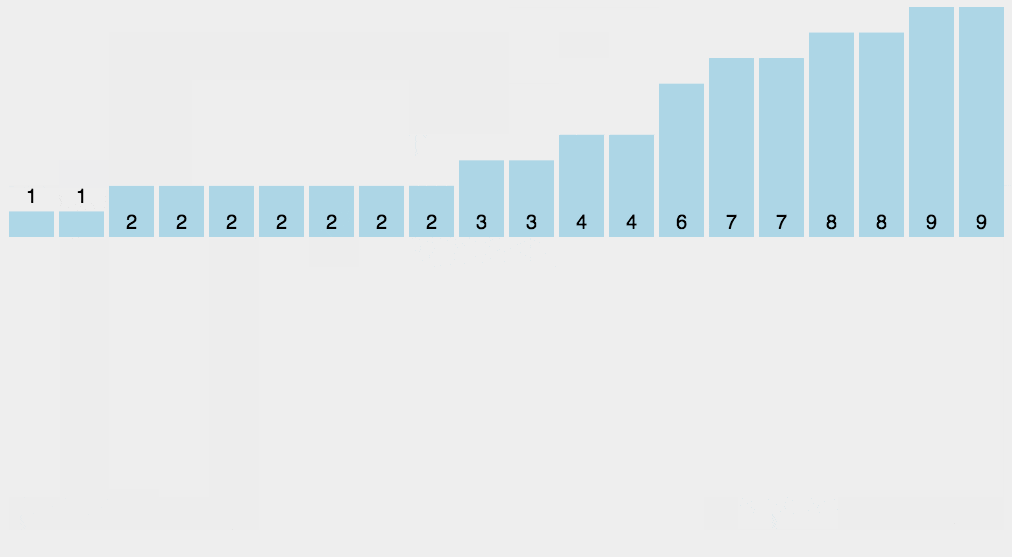
下面我们来详细的介绍一下这个排序的内容

❤️概念

计数排序是一个非基于比较的排序算法，元素从未排序状态变为已排序状态的过程，是由额外空间的辅助和元素本身的值决定的。该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为 $O(n+k)$（其中k是整数的范围），快于任何比较排序算法。

当然这是一种牺牲空间换取时间的做法，而且当 $O(k)>O(nlogn)$ 的时候其效率反而不如基于比较的排序，因为基于比较的排序的时间复杂度在理论上的下限是 $O(nlogn)$。

🧡算法思路

计数排序对输入的数据有附加的限制条件：

1、输入的线性表的元素属于有限偏序集 S；

2、设输入的线性表的长度为 n，|S|=k（表示集合 S 中元素的总数目为 k），则 $k=O(n)$。

在这两个条件下，计数排序的复杂性为$O(n)$。

计数排序的基本思想是对于给定的输入序列中的每一个元素 x，确定该序列中值小于 x 的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定。

一旦有了这个信息，就可以将 x 直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有 17 个元素的值小于 x 的值，则 x 可以直接存放在输出序列的第 18 个位置上。

当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

💛算法过程

1. 根据待排序集合中最大元素和最小元素的差值范围，申请额外空间；
2. 遍历待排序集合，将每一个元素出现的次数记录到元素值对应的额外空间内；
3. 对额外空间内数据进行计算，得出每一个元素的正确位置；
4. 将待排序集合每一个元素移动到计算得出的正确位置上。

💚算法性能

时间复杂度
O(n+k)。

空间复杂度
O(k)。

稳定性
稳定。

//计数排序
void CountSort(int* a, int n)
{
    //初始化最大值、最小值
	int max = a[0];
	int min = a[0];
	
	//找到数组中的最大值
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
		else if (a[i] < min)
			min = a[i];
	}

	//设置数组范围
	int range = max - min + 1;

	//创建动态空间在堆上，等等记得释放
	int* Count = (int*)calloc(range, sizeof(int));
	if (Count == NULL)
	{
		perror("calloc fail");
		return;
	}

	//记录每个数出现的次数
	for (int i = 0; i < n; i++)
	{
		Count[a[i] - min]++;
	}

	//写入排序好的数组
	int j = 0;
	for (int i = 0; i < n; i++)
	{
		while (Count[i]--)
		{
			a[j++] = i + min;
		}
	}

	//释放动态开辟空间
	free(Count);
	Count = NULL;
}

💙特别说明

虽然计数排序看上去很强大，但是它存在两大局限性：

1.当数列最大最小值差距过大时，并不适用于计数排序

比如给定 20 个随机整数，范围在 0 到 1 亿之间，此时如果使用计数排序的话，就需要创建长度为 1 亿的数组，不但严重浪费了空间，而且时间复杂度也随之升高。

2.当数列元素不是整数时，并不适用于计数排序

如果数列中的元素都是小数，比如 3.1415，或是 0.00000001 这样子，则无法创建对应的统计数组，这样显然无法进行计数排序。

正是由于这两大局限性，才使得计数排序不像快速排序、归并排序那样被人们广泛适用。

---

🏳️‍🌈基数排序

基数排序（Radix Sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。这种排序算法不是基于比较的排序算法，而是基于“分配”与“收集”。它适用于一定范围内的整数排序，且时间复杂度可以达到线性级别。

基数排序（Radix Sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表示字符串（如名字或日期）和特定格式的浮点数，基数排序并不是只能用于整数。这里是使用基数排序对数字进行排序的一个简单介绍。

基数排序按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别比较每个位数来工作，所以最低位（最右边）首先被使用。然后，如果两个数字的最低位相同，则比较它们的下一位。这个过程持续到最高位。

---

🏳️‍🌈桶排序

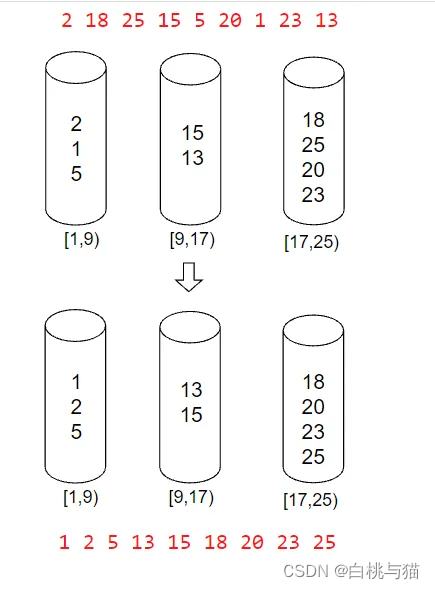
桶排序的思想就是把待排序的数尽量均匀地放到各个桶中，再对各个桶进行局部的排序，最后再按序将各个桶中的数输出，即可得到排好序的数。

1. 首先确定桶的个数。因为桶排序最好是将数据均匀地分散在各个桶中，那么桶的个数最好是应该根据数据的分散情况来确定。首先找出所有数据中的最大值mx和最小值mn；

2. 根据mx和mn确定每个桶所装的数据的范围 size，有
   size = (mx - mn) / n + 1，n为数据的个数，需要保证至少有一个桶，故而需要加个1；

3. 求得了size即知道了每个桶所装数据的范围，还需要计算出所需的桶的个数cnt，有
   cnt = (mx - mn) / size + 1，需要保证每个桶至少要能装1个数，故而需要加个1；

4. 求得了size和cnt后，即可知第一个桶装的数据范围为 [mn, mn + size)，第二个桶为 [mn + size, mn + 2 * size)，…，以此类推
   因此步骤2中需要再扫描一遍数组，将待排序的各个数放进对应的桶中。

5. 对各个桶中的数据进行排序，可以使用其他的排序算法排序，例如快速排序；也可以递归使用桶排序进行排序；

6. 将各个桶中排好序的数据依次输出，最后得到的数据即为最终有序。

---

👥总结

---

本篇博文对计数排序等做了一个较为详细的介绍，不知道对你有没有帮助呢

觉得博主写得还不错的三连支持下吧！会继续努力的~