桶排序(bucket sort)是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中;然后,在每个桶内部分别执行排序;最终按照桶的顺序将所有数据合并。
1. 实现步骤
● 计算桶数量:(最大值 - 最小值) / 数组长度 + 1 作为桶的数量是一种策略,可以根据数据的实际范围和数量来动态调整桶的数量 ,确保每个桶中的元素数量相对均匀,从而提高排序效率。
● 计算桶区间: 确保每个桶的区间大小合理分配,确保数据被均匀地分布在各个桶中。
●桶内数据进行排序
●依次输出桶中元素(即已排序数组)
2. 图解过程
举个栗子:
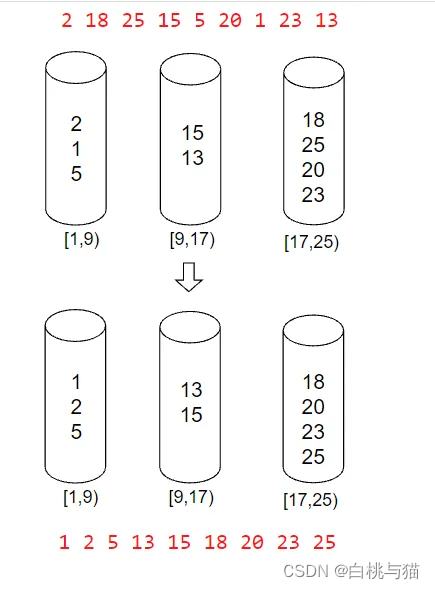
待排序数组 [2,18,25,15,5,20,1,23,13] , 分3个桶,将元素依次放入对应的桶中,再对每个桶内进行排序,最后按顺序输出。
3. 代码实现
function bucketSort(arr) {
const min = Math.min(...arr);
const max = Math.max(...arr);
// 计算桶数量
const bucketCount = Math.floor((max - min) / arr.length) + 1;
// 按桶数量创建相应的桶
const buckets = Array.from({ length: bucketCount }, () => []);
// 桶区间
const bucketRange = (max - min + 1) / bucketCount;
// 将元素放置在各个桶中
for (let val of arr) {
// num是每个桶的索引范围
let num = Math.floor((val - min) / bucketRange);
buckets[num].push(val);
}
// 对桶中元素再进行排序
for (const bucket of buckets) {
bucket.sort((a, b) => a - b); // 桶内元素可以使用其他排序方法,这里使用内置排序
}
// 输出
let i = 0;
for (const bucket of buckets) {
for (const item of bucket) {
arr[i++] = item;
}
}
4. 复杂度分析
● 时间复杂度:O(n)
● 空间复杂度:O(n)
● 自适应排序:在最差情况下,所有数据被分配到一个桶中,且排序该桶使用O(n^2) 时间。
● 非原地排序:需要借助桶变量
● 桶排序是否稳定取决于排序桶内元素的算法是否稳定
🔍时间复杂度的相关概念
🔍空间复杂度的相关概念
5. 桶排序适用场景
● 均匀分布的数据:桶排序在数据均匀分布的情况下表现最好,因为每个桶中的数据量大致相同。
● 已知数据范围:当数据范围已知且数据可以方便地分布到各个桶中时,桶排序非常有效。
● 数据量较大,但范围相对较小:桶排序可以有效地将数据分布到不同桶中进行排序。例如,有大量的数据点在某个有限的区间内。
6. 实际生活中使用场景
● 考试成绩排序:按成绩区间划分范围,统计前几名排行。
● 数据分析与统计:在市场分析、网站流量分析等领域,需要对大量数据进行分段统计(如年龄分布、访问量区间等),桶排序能高效地对数据进行初步分组和排序。
● 图像处理:在某些图像处理算法中,比如直方图均衡化,需要对像素强度进行统计和重新分配,桶排序可以用来高效地对像素值进行分组处理。