朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理与特征条件独立假设的分类方法。这种分类方法简单、高效，并且在很多实际场景中都有良好的表现。

1. 贝叶斯定理

贝叶斯定理是关于条件概率的定理，它描述了两个条件概率之间的关系。对于事件A和B，贝叶斯定理可以表示为：

其中，

• (P(A|B)) 是在事件B发生的情况下事件A发生的概率，即条件概率。
• (P(B|A)) 是在事件A发生的情况下事件B发生的概率。
• (P(A)) 和 (P(B)) 分别是事件A和事件B发生的概率。

2. 朴素贝叶斯分类器

朴素贝叶斯分类器基于一个假设：特征之间是相互独立的。这个假设虽然在实际中往往不成立（因此被称为“朴素”），但在很多情况下都能取得很好的效果。

在分类问题中，我们有：

• 一个特征向量 (X = {x_1, x_2, ..., x_n})
• 一个类别标签 (C)

我们的目标是找出给定特征向量 (X) 下，哪个类别标签 (C) 的概率最大，即求解 (P(C|X))。

根据贝叶斯定理，我们有：

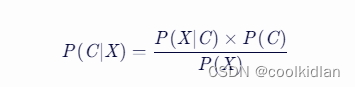
由于 (P(X)) 对于所有类别都是相同的，所以我们只需要比较 (P(X|C) \times P(C)) 的大小即可。

3. 特征条件独立假设

由于朴素贝叶斯假设特征之间是相互独立的，因此：

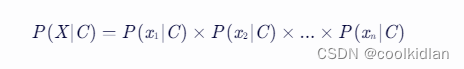
这个假设大大简化了计算，使得我们可以分别计算每个特征在给定类别下的条件概率。

4. 训练和分类

训练阶段：

• 计算每个类别在训练数据中的概率 (P(C))。
• 对于每个特征，计算该特征在每个类别下的条件概率 (P(x_i|C))。

分类阶段：

• 对于一个新的特征向量 (X)，计算每个类别下的 (P(X|C) \times P(C))。
• 选择 (P(X|C) \times P(C)) 值最大的类别作为预测结果。

5. 注意事项

• 特征条件独立假设虽然简化了计算，但在实际情况中往往不成立。这可能导致朴素贝叶斯在某些复杂数据集上表现不佳。
• 朴素贝叶斯对于离散特征有很好的处理效果，但对于连续特征，通常需要进行一些转换（如离散化或高斯近似）。
• 朴素贝叶斯对缺失值较为敏感，因此在处理缺失值时需要格外小心。
• 朴素贝叶斯分类器易于实现和解释，并且计算复杂度较低，因此在实际应用中非常受欢迎。