PID原理及控制算法详解

文章目录

1. 概念

1.1 PID框图

1.2 具体示例：无人机高度控制

2. PID原理

3. 常用术语

4. 计算过程

4.1 比例控制（Proportional）

4.2 积分控制（Integral）

4.3 微分控制（Derivative）

5. 代码实现逻辑

7. 串级PID和代码实现

6. 模拟仿真

1. 概念

PID是应用最广泛的闭环控制方法之一，是一种常用的反馈控制方法，对于每个PID控制器由三个部分组成：比例控制（Proportional）、积分控制（Integral）和微分控制（Derivative）。

一般而言，目标值和反馈值为同种物理量，输出值可以是施加在被控物体上的控制量
举例：对物体进行位置控制时，目标值=目标位置，反馈值=当前位置，输出值=施加的驱动力大小，PID就能实时计算出驱动力使物体到达目标位置。

控制程序一般会定时运行PID算法，在每次运行时，先计算出误差=目标值-反馈值，然后分别由P、I、D三个环节根据误差计算出输出分量，三个分量加和即为最终输出值。

1.1 PID框图

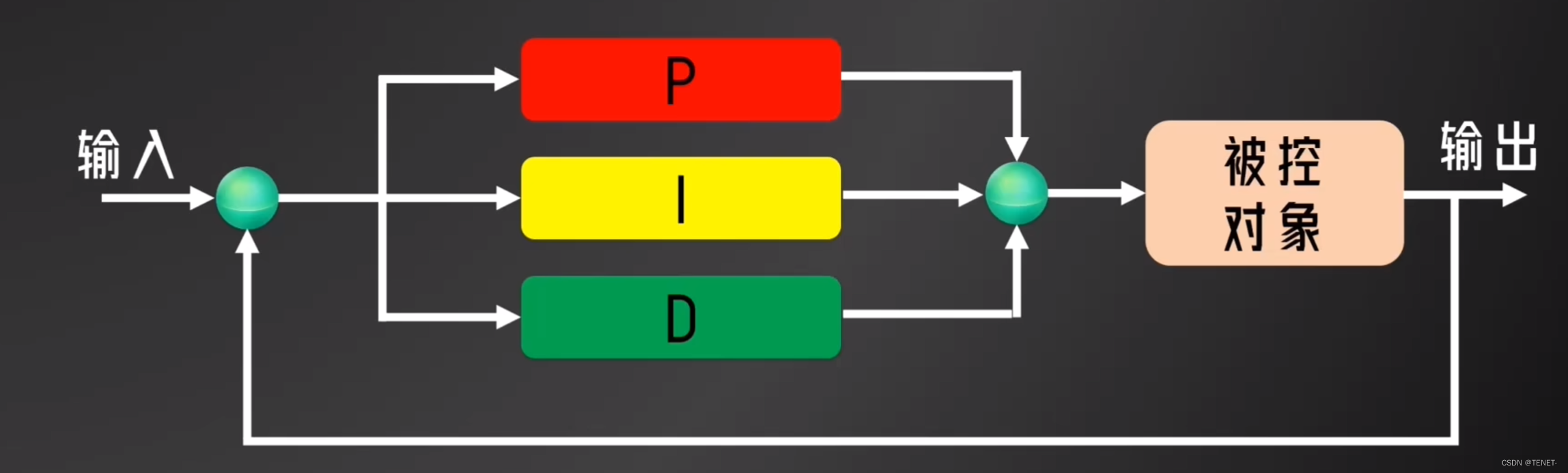
上图就是PID的信号框图，表示了PID的运行过程：

为系统指定一个目标值。PID将目标值与被控对象（无人机）当前的反馈量作差得到误差。PID将误差值分别经过三个环节计算得到输出分量，三个分量加起来得到PID的输出。将PID的输出施加到被控对象上，使反馈量向目标值靠拢。

PID三个环节的作用

由控制无人机案例我们可以总结出PID三个环节各自的主要作用和效应：

比例环节：起主要控制作用，使反馈量向目标值靠拢，但可能导致振荡。
积分环节：消除稳态误差，但会增加超调量。
微分环节：产生阻尼效果，抑制振荡和超调，但会降低响应速度。

PID中物理量的设计

我们在设计PID时主要关注三个量：目标值、反馈值、输出值。PID会根据目标值和反馈值计算输出值。

需要强调的是，PID并不知道被控对象是什么，它仅负责进行数值计算，而我们——作为控制系统的设计者，就需要为PID指定这三个量所对应的实际物理量，这在不同的控制系统中是不一样的。

如何确定实际物理量

我为大家总结了一个常用准则：

目标值和反馈值：
- 通常为同种物理量，就是你需要控制的物理量。
输出值：
- 通常是直接驱动被控对象的控制量。
- 输出量作用在被控对象上需要经过时间积累才会产生反馈量的变化，换言之，输出值通常为反馈值对于时间的低阶物理量。例如：目标值和反馈值为位置，则输出值可以为速度或加速度。

对于线性关系的两个物理量（只差一个系数），可以直接替换。例如：目标和反馈值为无人机的位置，根据上一条准则，输出值可以为加速度。但我们无法直接控制加速度，只能控制推力大小，由于由于高度的变化是由推力产生的，且推力与加速度只差一个系数（F=ma），因此可以将输出值直接定为推力。

1.2 具体示例：无人机高度控制

目标值（Setpoint）：无人机希望达到的高度，例如10米。
反馈值（Measured Value）：无人机当前的实际高度，例如8米。
误差（Error）：
- 目标高度与实际高度的差值。误差 = 目标高度 - 实际高度 = 10米 - 8米 = 2米。
输出值（Output）：
- 控制电机的推力大小，以使无人机的高度向目标高度靠拢。
- 由于推力与加速度成正比，我们可以将输出值设为推力。通过调整推力来改变无人机的加速度，从而改变高度。

2. PID原理

这是一个通过PID控制水管进出水流量的例子。让我们详细解释这个例子：

图示说明

阀门：水管中间有一个阀门，通过调节阀门的开度来控制水流量。
PID控制器：控制系统通过PID控制器来调节阀门，以控制水流量。
流量传感器：水管上有流量传感器，用来测量当前的实际流量。

工作原理

设定值：系统有一个预期流量值（设定值），这是希望达到的水流量。比如2L/S.
测量值：流量传感器实时测量当前的实际流量。
误差计算：PID控制器将实际流量与预期流量进行比较，得到误差值（误差 = 预期流量 - 实际流量）。
控制输出：
- 比例控制（P）：根据当前误差值直接调节阀门的开度。误差越大，调整幅度越大。
- 积分控制（I）：根据误差随时间的累积来调节阀门，以消除持续的偏差。积分控制能消除系统的稳态误差。
- 微分控制（D）：根据误差变化的速度来调节阀门，预见并平滑误差的变化，减少超调和振荡。

实际操作

启动时：当系统启动时，PID控制器根据初始误差进行较大的调整，使流量迅速接近设定值。
稳定阶段：当实际流量接近设定值时，比例控制器的作用减小，积分控制器确保误差归零，微分控制器平滑误差变化，避免波动。
扰动响应：当系统受到外部扰动（如水压变化）时，PID控制器会重新计算误差，并调整阀门，以重新达到设定的流量值。

3. 常用术语

被控对象：需要控制的对象。例如，温度控制中的加热器、速度控制中的电机等。
目标值（Setpoint）：期望被控对象达到的状态量。例如，温度控制中的期望温度、速度控制中的目标速度。
反馈值（Measured Value）：被控对象当前时刻的状态量。例如，当前的温度、当前的速度。
增益（Gain）：比例、积分和微分部分的放大系数，分别是Kp、Ki和Kd。
输出量（Output）：PID的计算结果，用于调整被控对象的控制力。例如，加热器的功率、驱动电机的电压。
误差（Error）：目标值与反馈值之间的差异。公式为：误差 = 目标值 - 反馈值。
稳态误差（Steady-State Error）：系统在稳定状态下仍然存在的误差。例如，加入干扰后仍存在的误差。
阶跃输入（Step Input）：在系统稳定状态下，目标值发生突然变化。例如，目标温度从20°C突然升高到25°C。
阶跃响应（Step Response）：阶跃输入后，被控对象的响应状态，能够代表系统的控制性能。
瞬态响应（Transient Response）：系统从初始状态到达到稳态的过渡过程，包括上升时间、超调量和调节时间等。
响应速度（Response Speed）：阶跃输入后，被控对象再次到达目标值的速度。
超调量（Overshoot）：阶跃输入后，被控对象到达目标值后超出目标值的距离。

4. 计算过程

这里用无人机的高度控制来举例

4.1 比例控制（Proportional）

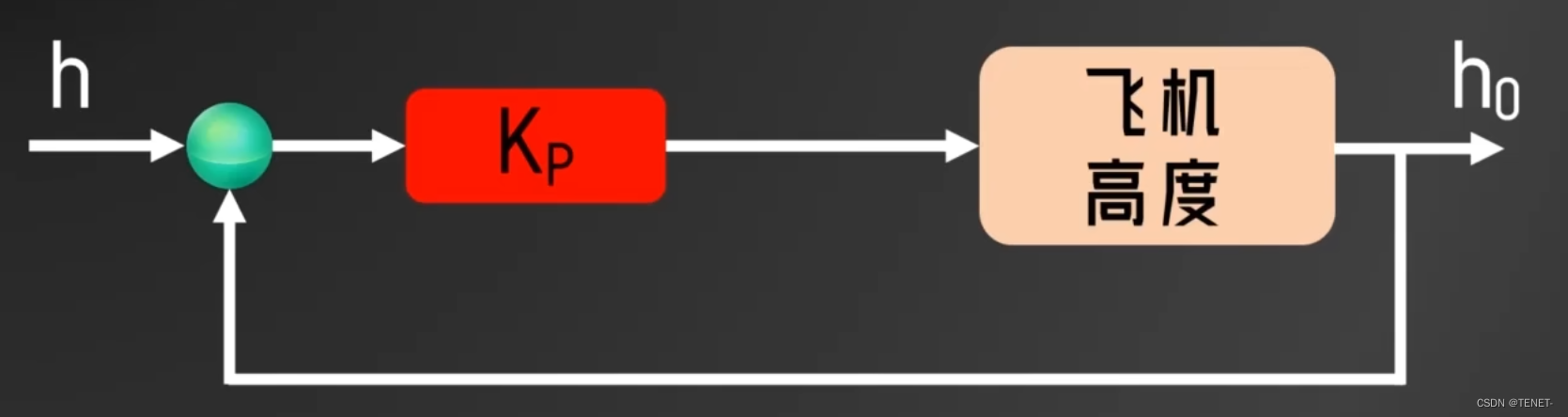
假如让无人机悬停在10米的高度，但此时高度为2米，所以此时误差(error)为8米，假设Kp=0.5，比例控制每次调节的高度就为：

Kp * error

所以第一次调节为 0.5*8=4，此时误差变为4米。

第二次调节：0.5*4=2，此时误差变为2米。

依次进行调节，误差逐渐变小。这个过程就叫做比例调节。

Kp值越大，系统反应速度越快，无人机更快靠近误差。

但是比例控制的缺点为两点：

干扰：容易受到外界干扰，比如此时有持续的风将无人机向下吹，导致无人机同一周期向下1米，此时比例控制的计算结果为0.5*2=1，所以，这会导致无人机永远保持在八米的高度，误差保持在2米。这也叫做稳态误差。
震荡：Kp值越大，系统反应速度越快，无人机更快靠近误差，但同时无人机在接近目标高度时，产生的震荡也越严重。

为了消除稳态误差的问题，就需要用到积分控制（Integral）。

为了消除系统震荡的问题，就需要用到微分控制（Derivative）。

4.2 积分控制（Integral）

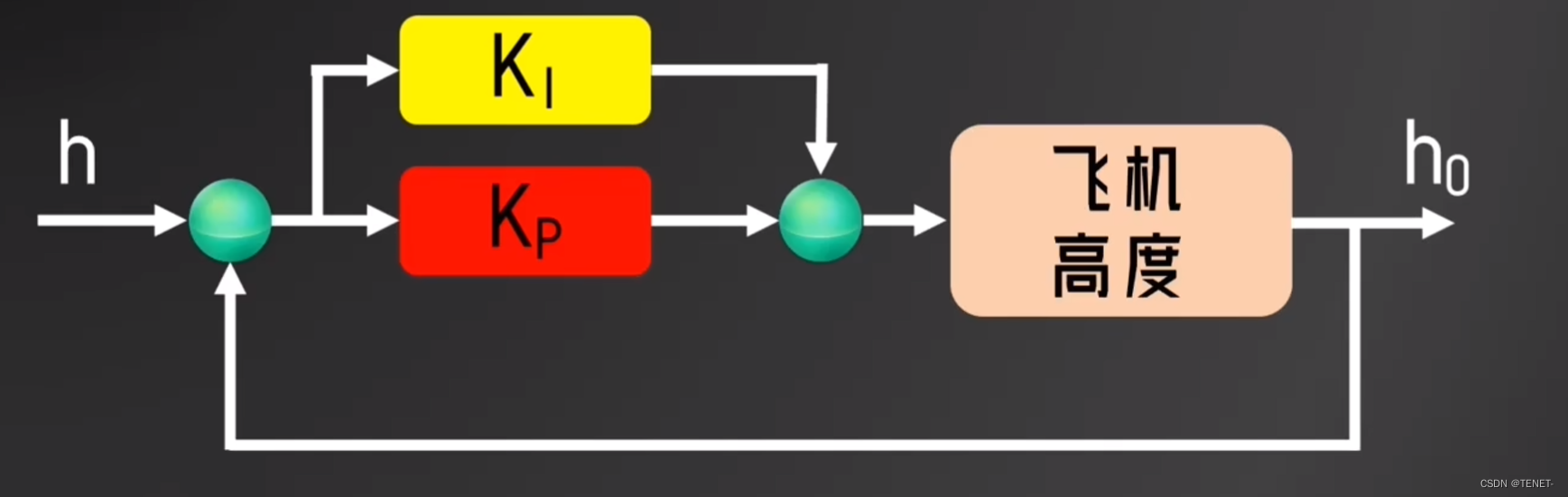
积分控制是对之前计算的所有的误差求和，也就是在离散的情况下做累加，比如无人机经过两次调节，第一次误差为8米，第二次误差为4米，加起来就是12米，假如Ki=0.1，计算结果为：

0.1*12=1.2，所以及时有向下持续的风影响无人机，由于积分控制，无人机还是会向上走1.2米。

所以积分控制会对误差进行累计，从而提供更大的升力，让无人机慢慢的朝着目标点靠近，最终误差消除为0。

所以经过第三次调节，累计误差从12调整到了12.8，那么第四次调节的结果0.1*12.8=1.28。

但此时无人机距离目标高度仅为0.8米，如果还是调节1.28米，就会出现过冲现象。

此时就需要使用微分控制进行更细致的调节。

4.3 微分控制（Derivative）

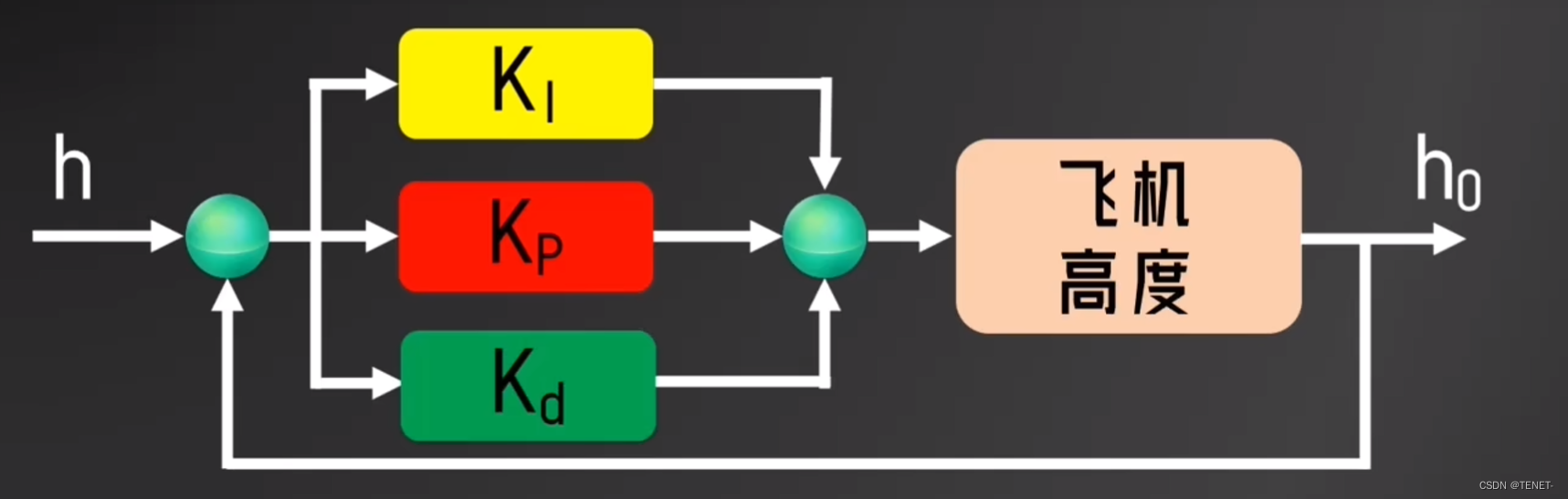
微分控制就是通过当前时刻与前一刻误差量的差值对未来做预测。如果差值为正，就表示误差在变大，为负就表示误差在减小。如果误差在变大，就会加大控制强度，让误差降下来。如果误差减小，就会减小控制强度，让无人机平稳缓和的到达指定值。

这里也就相当于对距离求微分：

d(error)/dt = 速度

微分控制算法可以对无人机的速度做出响应，当无人机的速度过快时，微分控制会抵消一部分由比例控制计算出来的升力，从而减缓系统的震荡。所以当我们提高Kd的值，系统的震荡会逐步减小。

但无论是比例，积分还是微分控制，数值调的过大，无人机就会出现过冲现象。

5. 代码实现逻辑

这段伪代码实现了一个基本的PID控制算法。

previous_error := 0
integral := 0

loop:
    error := setpoint - measured_value //计算误差
    integral := integral + error * dt //计算积分
    derivative := (error - previous_error) / dt //计算微分
    output := Kp * error + Ki * integral + Kd * derivative //计算控制输出
    previous_error := error //更新前一次误差
    wait(dt) //等待并循环
    goto loop