代码随想录--二叉树章节总结Part IV 完结篇

news2024/9/27 19:18:39

代码随想录–二叉树章节总结Part IV 完结篇🎉

1.Leetcode501 二叉树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

  • 结点左子树中所含节点的值 小于等于 当前节点的值
  • 结点右子树中所含节点的值 大于等于 当前节点的值
  • 左子树和右子树都是二叉搜索树

解题思路1: 利用Map。这种方法并没有利用到二叉搜索树的特性。首先对二叉树进行遍历，然后将出现的频率都保存的Map中。然后再次遍历二叉树，在Map中找到出现的频率最高的次数。最后再遍历一次二叉树，根据最高的出现次数，将元素从Map中找出来。这种方法很简单，但是很繁琐，代码就不放了。

解题思路2： 利用双指针，第一次遍历二叉树利用一个全局变量记录最大的出现次数。第二次再次遍历二叉树，找到出现次数和最大出现次数相等的结点，然后保存到结果集中，最后输出。

private TreeNode pre;
private ArrayList<Integer> list = new ArrayList<>();
private int count = 0;
private int maxCount = 0;
private  void inorder(TreeNode root) {
    if (root == null) return;
    inorder(root.left);

    if (pre == null) {
      	count = 1;
    } else if (pre.val == root.val) {
      	count++;
    } else {
      // 前后val不同，复位count;
      	count = 1;;
    }
    pre = root;
    // 判断maxCount和count
    if (count > maxCount) {
      	maxCount = count;
    }

    inorder(root.right);
}
private void inorder1(TreeNode root) {
    if (root == null) return;
    inorder1(root.left);

    if (pre == null) {
      	count = 1;
    } else if (pre.val == root.val) {
      	count++;
    } else {
      // 前后val不同，复位count;
      	count = 1;;
    }
    pre = root;
    // 判断maxCount和count
    if (count == maxCount) {
      	list.add(root.val);
    }

    inorder1(root.right);
}
public int[] findMode(TreeNode root) {
    // 第一遍遍历 找出出现的最大频率次数
    inorder(root);
    System.out.print(maxCount);
    // 将所有变量归0，然后进行第二次遍历
    pre = null;
    count = 0;
    // 第二遍遍历 根据maxCount找出元素加入结果集
    inorder1(root);
    System.out.print(list);
    int[] res = new int[list.size()];
    for (int i = 0; i < res.length; i++) {
      	res[i] = list.get(i);
    }
    return res;
}

解题思路3: 只需要一次中序遍历即可。

  • 创建全局变量pre用于指向前一个元素，创建结果集list，创建count用于记录当前遍历元素的出现频率，maxCount用于记录最大的出现频率
  • 然后开始遍历二叉树，如果pre为空，说明当前遍历的是第一个结点，那么count = 1
  • 如果pre不为空，并且pre的值和当前遍历的结点值相等，则count++
  • 如果pre和当前结点的值不相等，则count = 1。比如pre = 4 root = 5，那么count = 1指的是5出现了1次
  • 计算完count之后，还需要和maxCount比较，如果count比maxCount大，则需要maxCount = count, 其次还需要清空之间list中保存的元素，并将当前加入到list中。清空list原因是list中保存到出现频率都是count的，而现在当前元素出现的频率要大于count，所以直接保存的都失效了
  • 最后返回结果集
private TreeNode pre;
private ArrayList<Integer> list;
private int count = 1;
private int maxCount = 1;
private void inorder(TreeNode root) {
    if (root == null) return;
    inorder(root.left);

    if (pre == null) {
      	count = 1;
    } else if (pre.val == root.val) {
      	count++;
    } else {
      // 前后val不同，复位count;
     	 count = 1;;
    }
    // 判断maxCount和count
    if (count > maxCount) {
        maxCount = count;
        list.clear();
        list.add(root.val);
    } else if (count == maxCount) {
      	list.add(root.val);
    }
    inorder(root.right);
  }

public int[] findMode(TreeNode root) {
    inorder(root);
    int[] res = new int[list.size()];
    for (int i = 0; i < res.length; i++) {
      	res[i] = list.get(i);
    }
    return res;
}

2.Leetcode236 二叉树最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

img

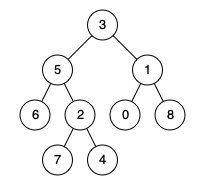
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

解题思路1: 利用递归的后序遍历来做。

  • 首先判断遍历结点是否为空，如果为空，则返回空
  • 然后判断遍历结点是否是要查找的p或者q，如果是则直接返回
  • 否则就去递归的搜索左右子树
  • 如果左右子树有一个返回值为空，就把另一个不为空的返回
  • 如果都不为空，则说明当前结点就是公共祖先
  • 如果都为空，则返回null，说明没有查找到
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null) return root;
    // 如果正好遇到了p和q，那么直接返回p和q即可
    if (root == p || root == q) return root;
    // 后序遍历左右子树
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);

    // 如果左右子树都不为空，则说明当前遍历到的结点就是公共祖先
    if (left != null && right != null) return root;
    if (left == null && right != null) return right;
    if (left != null && right == null) return left;
    // 如果都为空，则说明找不到公共祖先
    return null;
}

下面通过举例子来说明：

image-20230129162600558

  • 情况1:
    • 根据后序遍历，遍历结点1，结点1不满足if (root == p || root == q) return root;条件，因此会继续递归调用，然而结点1左右子树都为空，相当于调用了lowestCommonAncestor(null, p, q);最后返回空，所以结点1的左右子树返回值都为空，所以结点1返回空。
    • 然后判断结点6正好是要查找到的结点，则直接返回。5同理。执行的返回代码是if (root == p || root == q) return root;所以对于结点7来说，左右子树返回值都不为空，则直接返回7
    • 对于结点10，左边结点1的返回值是空，右边返回值是7，所以结点10的返回值是7
    • 对于根的右子树来说，结点15和结点20原理和结点1一样，都返回空，所以结点4也返回空
    • 最终，对于根结点8来说，左子树返回7，右子树返回空，所以最终结果是返回7
  • 情况2:
    • 当递归到结点7的时候，由于7正好是要查找的元素，所以直接返回。
    • 对于结点10，左边结点1的返回值是空，右边返回值是7，所以结点10的返回值是7
    • 对于根的右子树来说，结点15和结点20原理和结点1一样，都返回空，所以结点4也返回空
    • 最终，对于根结点8来说，左子树返回7，右子树返回空，所以最终结果是返回7
    • 也就是说情况2中，结点5，6根本没有进行遍历

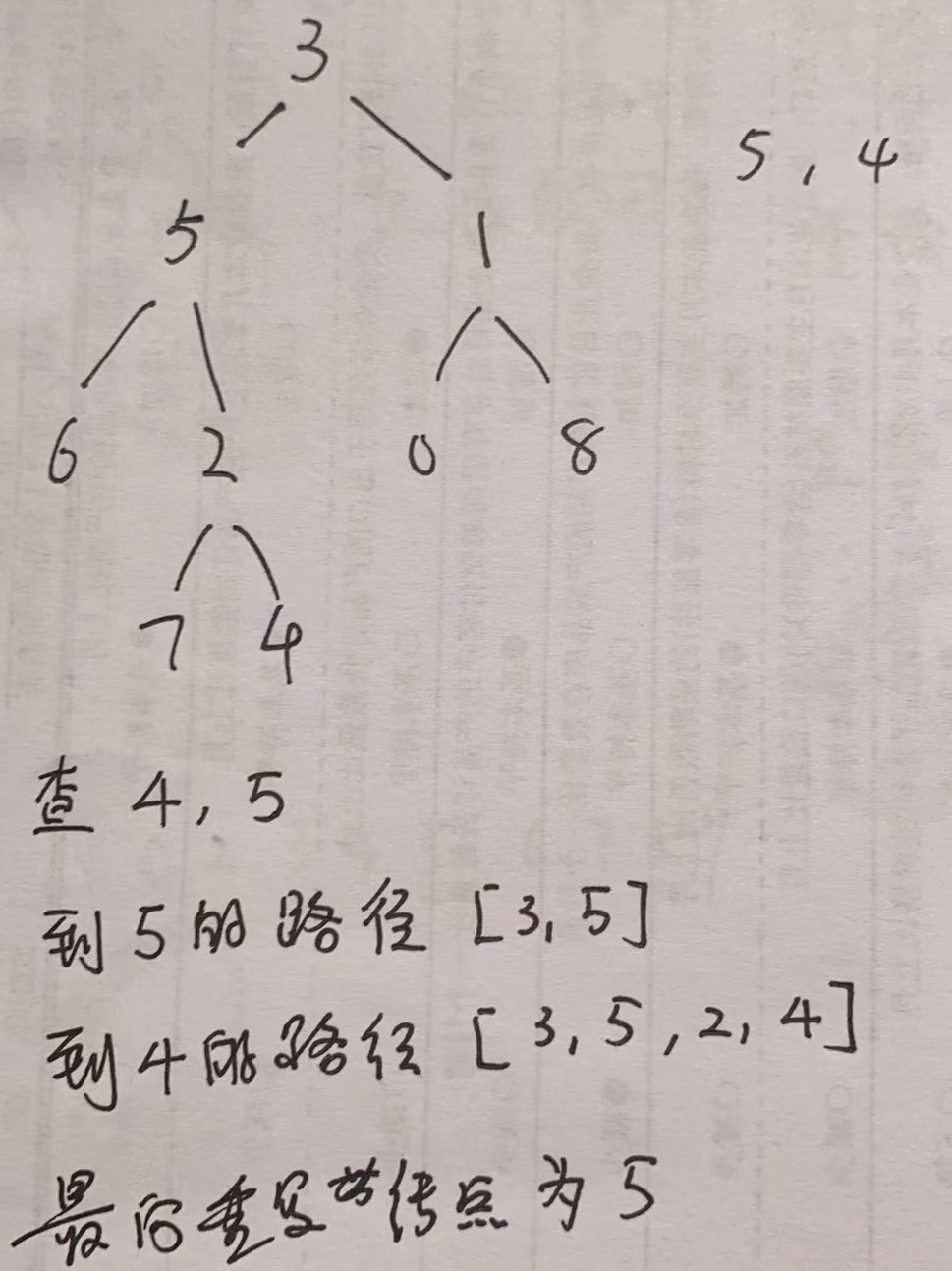
解题思路2: 利用层序遍历获取从根结点到p，q结点的路径。然后遍历两个路径，找到两个路径中最后相同的结点，这个结点就是公共祖先。

image-20230129174511972

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // 如果树为空或者只有一个结点
    if (root == null || (root.left == null && root.right == null)) return root;
    // 利用层序遍历，记录到p，q的路径
    Queue<TreeNode> nodeQ = new LinkedList<>();
    Queue<ArrayList<TreeNode>> pathQ = new LinkedList<>();
    ArrayList<ArrayList<TreeNode>> res = new ArrayList<>(2);
    // 根结点入队
    nodeQ.offer(root);
    pathQ.offer(new ArrayList<>(Arrays.asList(root)));
    while (!nodeQ.isEmpty()) {
        TreeNode node = nodeQ.poll();
        ArrayList<TreeNode> path = pathQ.poll();
        if (node == p || node == q) {
          	res.add(path);
        }
        if (node.left != null) {
            nodeQ.offer(node.left);
            ArrayList<TreeNode> left = new ArrayList<>(path);
            left.add(node.left);
            pathQ.offer(left);
        }
        if (node.right != null) {
            nodeQ.offer(node.right);
            ArrayList<TreeNode> right = new ArrayList<>(path);
            right.add(node.right);
            pathQ.offer(right);
        }
    }
    // 当循环结束，可以获取到到p，q的路径
    ArrayList<TreeNode> path1 = res.get(0);
    ArrayList<TreeNode> path2 = res.get(1);
    TreeNode ret = null;
    int i = 0, j = 0;
    while (i < path1.size() && j < path2.size()) {
        if (path1.get(i) == path2.get(j)) {
            ret = path2.get(j);
        }
        i++;
        j++;
    }
    return ret;
  }

3.Leetcode235 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

解题思路1: 利用BST性质直接从根结点开始搜索。

img

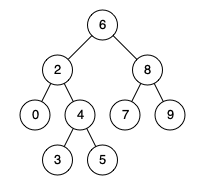
举个例子更容易说明问题。假设我们要搜索的结点是3，5。

  • 那么从根结点6开始，因为6是大于max(3,5)，所以继续在左子树搜索公共祖先。
  • 然后判断2，2是大于min(3,5)，所以继续搜索右子树
  • 遍历到结点4，因为4属于(3,5)区间之间，所以4就是最近公共祖先。

这里还有一种情况，假设我们搜索的结点是4和5，那么遍历到2结点，因为2小于min(4,5)，所以遍历右子树。然而此时判断4是否位于(4,5)区间时，上述的几种判断条件都不成立，进入死循环，如下面的代码：

while (cur != null) {
    if (cur.val > min && cur.val < max) return cur;
    if (cur.val < min) cur = cur.right;
    else if (cur.val > max) cur = cur.left;
}

因此我们在判断的时候，还需要加一个条件，就是如果遍历的这个结点就等于p或者q，那么直接返回这个结点就可以了。

if (cur.val == min || cur.val == max) return cur;

所以完整版的代码如下：

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  // 如果树为空或者只有一个结点 
    if (root == null || (root.left == null && root.right == null)) return root;
    TreeNode cur = root;
    // 每次都比较当前遍历到的元素的值和qp值关系
    int max = Math.max(p.val, q.val);
    int min = Math.min(p.val, q.val);

    while (cur != null) {
        if (cur.val == min || cur.val == max) return cur;
        if (cur.val > min && cur.val < max) return cur;
        if (cur.val < min) cur = cur.right;
        else if (cur.val > max) cur = cur.left;
    }
    return null;
}

三种情况的图示如下：

image-20230129170752211

当然，这个题使用二叉树的求公共祖先的代码也可以

4.Leetcode701 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。输入数据保证 ，新值和原始二叉搜索树中的任意节点值都不同。

解题思路： 首先需要知道的是，BST中插入结点，那么这个结点一定是叶子结点。其次就是按照手工插入结点的方式进行代码模拟即可。

需要注意的是，当我们通过比较root的val和输入的val来确定往左还是往右走的时候，需要先判断一下左或者右是否为空，如果为空，则这个空的位置就是要插入的位置。

而指针正好指向要插入结点的父结点，因此非常好插入。

public TreeNode insertIntoBST(TreeNode root, int val) {
    if (root == null) return new TreeNode(val);
    TreeNode cur = root;
    while (cur != null) {
        if (cur.val > val) {
            // 应该往左遍历
            if (cur.left != null)
              	cur = cur.left;
            else {
              // 如果左边为空了，则说明这个地方需要插入新结点
                cur.left = new TreeNode(val);
                break;
            }
          } else {
              if (cur.right != null)
                	cur = cur.right;
              else {
                  // 如果左边为空了，则说明这个地方需要插入新结点
                  cur.right = new TreeNode(val);
                  break;
              }
        }
    }
    return root;
}

采用相同的思路的递归版本代码如下：

public TreeNode insertIntoBST(TreeNode root, int val) {
    if (root == null) return new TreeNode(val);
    if (root.val > val) {
        TreeNode left = insertIntoBST(root.left, val);
        root.left = left; // 新结点的连接
    } else {
        TreeNode right = insertIntoBST(root.right, val);
        root.right = right;
    }
    return root;
}

5.Leetcode450 删除BST中的结点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：首先找到需要删除的节点；如果找到了，删除它。

解题思路： 删除BST中的结点有5中情况。

  • 要删除的结点不存在
  • 若要删除的结点是叶子结点，则直接删除
  • 要删除的结点只有左边有元素，右边为空，则直接将要删除的元素的左子树赋值给要删除元素的父结点的左孩子即可。
  • 要删除的结点只有右边有元素，左边为空，则直接将要删除的元素的右子树赋值给要删除元素的父结点的右孩子即可。
  • 要删除的结点左右都有不为空，则需要将要删除结点的左子树，赋值给要删除结点的右子树中最左边元素的左子树上。

image-20230129201813019

public TreeNode deleteNode(TreeNode root, int key) {
    // 如果这个树是空树 或者BST中不存在key的结点，返回空
    if (root == null) return root;
    // 如果不是空树
    if (root.val == key) {
        // 存在要删除的结点
        // 如果要删除的结点是叶子结点，中直接返回空
        if (root.left == null && root.right == null)
          return null;
        // 如果要删除的结点是左边不为空，右边为空
        if (root.left != null && root.right == null)
          return root.left;
        // 如果要删除的结点是左边为空右边不为空
        if (root.left == null && root.right != null)
          	return root.right;
        // 如果左右都不为空
        if (root.left != null && root.right != null) {
          // 首先获取到要删除结点右子树最左边的元素
            TreeNode cur = root.right;
            while (cur.left != null) cur = cur.left;
            cur.left = root.left;
            return root.right;
        }
    }
    if (root.val > key)
      	root.left = deleteNode(root.left, key);
    if (root.val <key)
      	root.right = deleteNode(root.right, key);
    return root;
}

在这个题中，是使用递归的返回值来实现元素的删除的。

image-20230129202348710

6.Leetcode669 修剪BST

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

public TreeNode trimBST(TreeNode root, int low, int high) {
    if (root == null) return null;
    if (root.val < low) {
        TreeNode left = trimBST(root.right, low, high);
        return left;
    }
    if (root.val > high) {
        TreeNode right = trimBST(root.left, low, high);
        return right;
    }
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
}

递归过程图解：

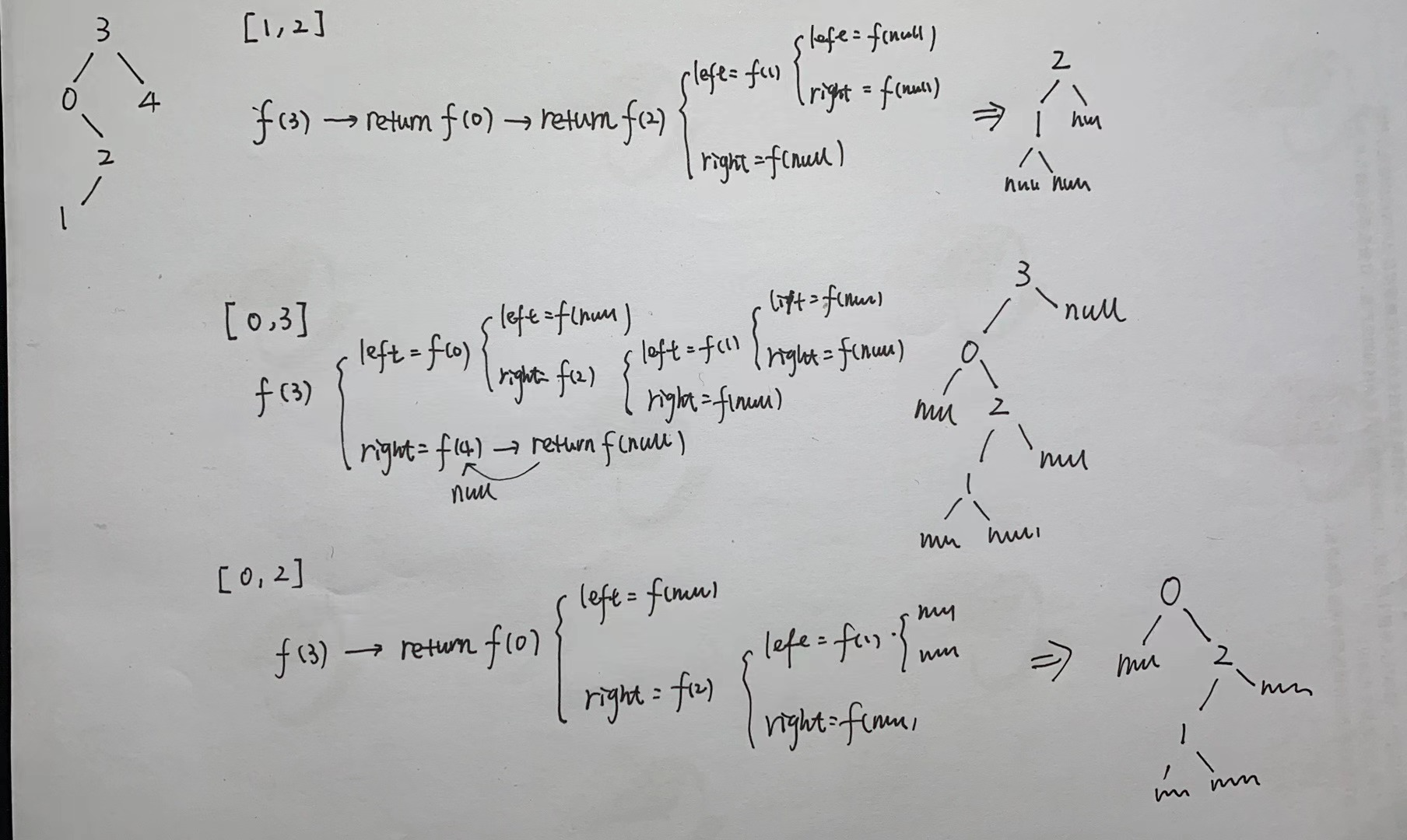
image-20230129222007059

总结一下：通过return来删除元素，通过root.left = trimBST来连接元素

7.Leetcode108 将有序数组转化为BST

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

这个题一开始考虑的时候都在想如何保证为平衡二叉树，但是实际上按照数组去中间元素然后递归的方法构建的BST本身就是平衡的。

这里强调平衡是因为升序的数组也可以构建为一个链表，这个链表也可看作二叉树。本题提出平衡二叉树就是为了避免构建出这种单链表形势的二叉树。

解题思路： 直接取数组中的中间元素作为根结点，然后将数组划分为两部分，然后递归的构建左右子树即可。另外如果数组长度为偶数，那么中间结点选左边还是右边都可以。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MdHMJYBB-1675019361383)(https://code-thinking.cdn.bcebos.com/pics/108.%E5%B0%86%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E8%BD%AC%E6%8D%A2%E4%B8%BA%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.png)]

public TreeNode sortedArrayToBST(int[] nums) {
  	return f(nums, 0, nums.length - 1);
}

private TreeNode f(int[] nums, int left, int right) {
    if (left > right) return null;
    if (left == right) return new TreeNode(nums[left]);

    int mid = (left + right) / 2;
    TreeNode root = new TreeNode(nums[mid]);
    root.left = f(nums, left, mid - 1);
    root.right = f(nums, mid + 1, right);
    return root;
}

这个题本质上和通过前序序列和中序序列构建二叉树的题是一样的。

8.Leetcode538 把二叉搜索树转化为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

解题思路：

  • 首先遍历一边二叉树，计算出所有的叶子叶子结点之和total。
  • 然后再次中序遍历二叉树，第一个结点的值就是total
  • 对于其他结点来说，它的值等于total - 其前驱结点的val(未累加的值)。
private int total = 0;
private Integer preVal = null;
public TreeNode convertBST(TreeNode root) {
    // 第一次中序遍历二叉树 统计所有结点val之和
    inorder(root);
    inorderAgain(root);
    return root;
}
private void inorder(TreeNode root) {
  // 中序遍历二叉树 统计所有结点val之和
    if (root == null) return;
    inorder(root.left);
    total += root.val;
    inorder(root.right);
}
private void inorderAgain(TreeNode root) {
    if (root == null) return;
    inorderAgain(root.left);
    // 如果是第一个元素
    if (preVal == null) {
        preVal = root.val;
        root.val = total;
    } else {
        total -= preVal;
        preVal = root.val;
        root.val = total;
    }
    inorderAgain(root.right);
}

图解过程：

image-20230130023014538

后记：

现在是1月30号凌晨3点06，从1月14号开始刷代码随想录，一共耗时半个月的时间，系统性的学习了数组，队列，栈，链表，哈希表，双指针，二叉树。这次刷题只刷了例题，扩展到题目并没有刷，二刷的时候不上。另外对于一些高级的算法，如贪心等，后序有机会再会。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/186621.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

大数据行业如何获取高薪岗位offer？

大数据行业如何获取高薪岗位offer？

在互联网行业需要保持不断的学习。学习大数据先思考自身未来想往哪个方向发展&#xff0c;想要入门快、基础深厚&#xff0c;并且需求多应用广建议从JAVA开始学起&#xff0c;找到适合自己的学习方法。 大数据行业人才稀缺&#xff0c;据第三方统计2020年全国招收程序员394699…
阅读更多...
mybatis-plus2

mybatis-plus2

目录 一、乐观锁 二、乐观锁与悲观锁的区别 1.乐观锁和悲观锁的应用场景 三、条件查询构造器 四、分页查询 五、逻辑删除 六、在Mybatis-plus中使用xml配置 一、乐观锁 乐观锁插件 | MyBatis-PlusMyBatis-Plus 官方文档https://baomidou.com/pages/0d93c0/ 当要更新一条…
阅读更多...
16. JSON解析

16. JSON解析

1. 什么是 JSON &#xff1f; JSON 指的是 JavaScript 对象表示法&#xff08;JavaScript Object Notation&#xff09;。 JSON 是轻量级的文本数据交换格式。 JSON 独立于语言&#xff1a;JSON 使用 Javascript语法来描述数据对象&#xff0c;但是 JSON 仍然独立于语言和平台…
阅读更多...
Kettle基础操作

Kettle基础操作

目录 Kettle基础操作 1 启动Kettle 2 创建本地资源库 3 基础操作 3.1 新建转换 3.2 新建作业 3.3 节点连接 4 导入/导出资源库 5 创建数据库连链接 Kettle基础操作 1 启动Kettle 前置环境&#xff1a;JDK 1.7以上、IE浏览器升级至IE10以上&#xff08;Kettle7.0以下…
阅读更多...
Java——打家劫舍

Java——打家劫舍

题目链接 leetcode在线oj题——打家劫舍 题目描述 你是一个专业的小偷&#xff0c;计划偷窃沿街的房屋。每间房内都藏有一定的现金&#xff0c;影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统&#xff0c;如果两间相邻的房屋在同一晚上被小偷闯入&#xff…
阅读更多...
Hive数仓建设手册

Hive数仓建设手册

1 数仓的分层及建模理论 1.1 数据仓库的用途 整合公司所有业务数据&#xff0c;建立统一的数据中心产生业务报表&#xff0c;用于作出决策为网站运营提供运营上的数据支持可以作为各个业务的数据源&#xff0c;形成业务数据互相反馈的良性循环分析用户行为数据&#xff0c;通…
阅读更多...
MySQL中的正则表达式

MySQL中的正则表达式

目录 一.介绍 二.格式 三.操作 一.介绍 正则表达式(regular expression)描述了一种字符串匹配的规则&#xff0c;正则表达式本身就是一个字符串&#xff0c;使用这个字符串来描述、用来定义匹配规则&#xff0c;匹配一系列符合某个句法规则的字符串。在开发中&#xff0c;正…
阅读更多...
5G小区选择重选参数的设置

5G小区选择重选参数的设置

学习大唐杯的过程中的一些总结。 目录 前言 一、S准则 二、R准则 三、关于频点优先级 总结 前言 5G参数总体的设计思想是在总体成本的控制下&#xff0c;满足覆盖范围和容量的同时&#xff0c;达到5G各个小区之间正确进行通信。 一、S准则 在后续介绍的频点优先级中&#xff0…
阅读更多...
【多任务】任务损失/梯度优化策略合集

【多任务】任务损失/梯度优化策略合集

本文分享如何从loss和gradient方面，优化多任务模型，缓解负迁移或跷跷板的问题。不足之处，还望批评指正。 背景 最近工作中，有使用到多任务模型，但实际使用时，会面临负迁移、跷跷板等现象。 除了从模型角度优化，这里介绍从loss和gradient方面的优化
阅读更多...
SpringBoot创建接口

SpringBoot创建接口

目录 一、创建Spring Boot Project (一)配置Spring Boot (二)配置数据库连接&#xff0c;并启动tomcat 二、新建测试网页——这一步可以忽略&#xff0c;主要是测试配置是否成功 1.新建一个页面 2.创建TestController类 3.启动SpringbootpracticeApplication类——sprin…
阅读更多...
【Linux】makemakefile

【Linux】makemakefile

【Linux】make & makefile 文章目录【Linux】make & makefile1、makefile文件2、make命令3、make原理规则4、.PHONY5、编译与否的判断法1、makefile文件 makefile实际上是一个文件&#xff0c;配置文件 充当Linux上的工程管理工具&#xff0c;可以实现自动化编译 mak…
阅读更多...
transformer库的思想

transformer库的思想

transformer库建立思路 (1) Model类: 如BertModel , 目前收录有超过30个PyTorch模型或Keras模型; (2) Configuration类: 如BertConfig , 用于存储搭建模型的参数; (3) Tokenizer类: 如BertTokenizer , 用于存储分词词汇表以及编码方式; 使用from_pretrained()和save_pretraine…
阅读更多...
区块链知识系列 - 系统学习EVM(二)

区块链知识系列 - 系统学习EVM(二)

特点 EVM出于所谓运算速度和效率方面考虑&#xff0c;采用了非主流的256bit整数。不支持浮点数缺乏标准库支持,例如字符串拼接、切割、查找等等都需要开发者自己实现给合约打补丁或是部分升级合约代码在EVM中是完全不可能的 存储 Code code 部署合约时储存 data 字段也就是合…
阅读更多...
08-linux网络管理-iptables扩展模块

08-linux网络管理-iptables扩展模块

文章目录1. 概述2. icmp 模块2.1 示例&#xff08;禁止本机ping其它主机&#xff09;2.2 示例&#xff08;其他主机ping本机&#xff09;2.3 --icmp-type 说明3. iprange模块4. multiport 模块5. state 模块5.1 语法5.2 完整示例6. limit模块6.1 语法6.2 完整示例7. connlimit7…
阅读更多...
[2019红帽杯]easyRE1题解

[2019红帽杯]easyRE1题解

迷蒙马背眠&#xff0c;月随残梦天边远&#xff0c;淡淡起茶烟。 ——松尾芭蕉 目录 1.查壳 2.拖入64位IDA&#xff0c;找到主函数 3.静态分析主函数 4.wp 1.查壳 ELF文件&#xff0c;64bit 2.拖入64位IDA&#xff0c;找到主函数 没有标明main函数&#xff0c;我们打开str…
阅读更多...
OSCP_VULHUB COVFEFE: 1

OSCP_VULHUB COVFEFE: 1

文章目录前言信息收集渗透过程权限提升前言 靶机下载地址&#xff1a;https://www.vulnhub.com/entry/covfefe-1,199/ 攻击机&#xff1a;kali&#xff08;192.168.132.139&#xff09; 靶机&#xff1a;covfefe&#xff08;192.168.132.146&#xff09; 下载好靶机之后直接使…
阅读更多...
vivo 超大规模消息中间件实践之路

vivo 超大规模消息中间件实践之路

作者&#xff1a;vivo 互联网存储技术团队-Luo Mingbo、中间件团队- Liu Runyun 本文根据“2022 vivo开发者大会"现场演讲内容整理而成。 本文主要介绍超大数据规模场景下分布式消息中间件在vivo的应用实践。 在线业务侧主要从RocketMQ集群部署架构、平台系统架构、日常运…
阅读更多...
EMC基础：电容的频率特性

EMC基础：电容的频率特性

本文将对其中使用电容和电感降噪的对策进行介绍&#xff0c;这也可以称为“噪声对策的基础”。在这里使用简单的四元件模型。如果要进一步表达高频谐振时&#xff0c;可能需要更多的元件模型。 电容的频率特性 探讨利用电容器来降低噪声时&#xff0c;充分了解电容器的特性是…
阅读更多...
设计模式——软件设计原则

设计模式——软件设计原则

目录 3.软件设计原则 3.1 开闭原则 3.2 里氏代换原则 3.3 依赖倒转原则 3.4 接口隔离原则 3.5 迪米特法则 3.6 合成复用原则 3.软件设计原则 在软件开发中&#xff0c;为了提高软件系统的可维护性和可复用性&#xff0c;增加软件的可扩展性和灵活性&#xff0c;程序员要…
阅读更多...
8、Servlet——Servlet生命周期、Servlet特性

8、Servlet——Servlet生命周期、Servlet特性

目录 一、Servlet生命周期 1、生命周期的四个阶段 1.1 实例化 1.2 初始化 1.3 服务 1.4 销毁 2、Servlet执行流程 3、代码演示 二、 Servlet特性 1、线程安全问题 2、如何保证线程安全 一、Servlet生命周期 1、生命周期的四个阶段 1.1 实例化 当用户第一次访问Ser…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023