中点分割直线段裁剪算法

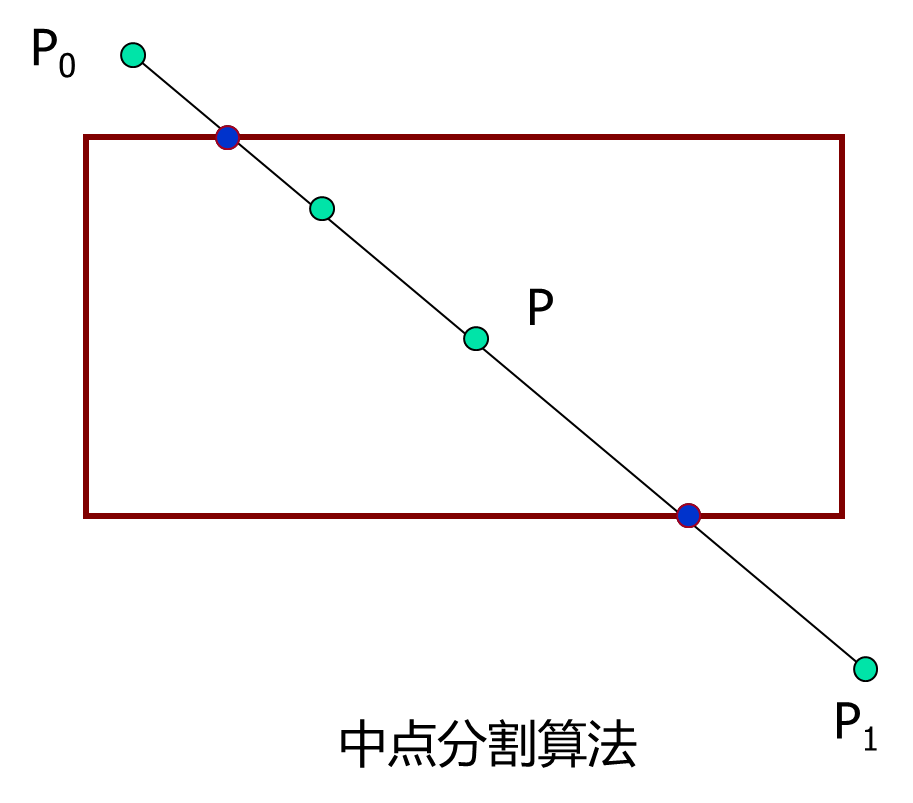
中点分割直线段裁剪算法对Cohen-Sutherland直线裁剪算法的第3种情况做了改进，

原理
在这里插入图片描述

中点计算公式

在这里插入图片描述

代码

BOOL CTestView::Cohen()//Cohen－Sutherland算法
{
	EnCode(P[0]);//起点编码
	EnCode(P[1]);//终点编码
	while(P[0].rc!=0 || P[1].rc!=0)
             {//处理至少一个顶点在窗口之外的情况
		if((P[0].rc & P[1].rc)!=0)//简弃之
		{
			PtCount=0;
			return FALSE;
		}
		if(0==P[0].rc)//确保P[0]位于窗口之外
		{
			CP2 Temp;
			Temp=P[0];
			P[0]=P[1];
			P[1]=Temp;
		}
		MidClip(P[0],P[1]);
	}
	return TRUE;
}

void CTestView::MidClip(CP2 p0,CP2 p1)//中点分割算法
{
	CP2 p;//中点坐标	
	p.x=(p0.x+p1.x)/2;p.y=(p0.y+p1.y)/2;EnCode(p);
	while(fabs(p.x-p0.x)>1e-6||fabs(p.y-p0.y)>1e-6)//判断结束
	{
		if(0==p.rc)//中点也在窗口内，则舍弃P0点
		      p1=p;
		else//否则舍弃P1点
		       p0=p;
		p.x=(p0.x+p1.x)/2;
                       p.y=(p0.y+p1.y)/2;
                       EnCode(p);
	}
	P[0]=p;
}

Liang-Barsky直线段裁剪算法⭐⭐⭐

80年代初梁友栋先生提出了著名的Liang-Barsky裁剪算法，通过线段的参数化表示实现快速裁剪，至今仍是计算机图形学中最经典的算法之一。

梁友栋与Barsky提出了比Cohen-Sutherland裁剪算法速度更快的直线段裁剪算法。

原理
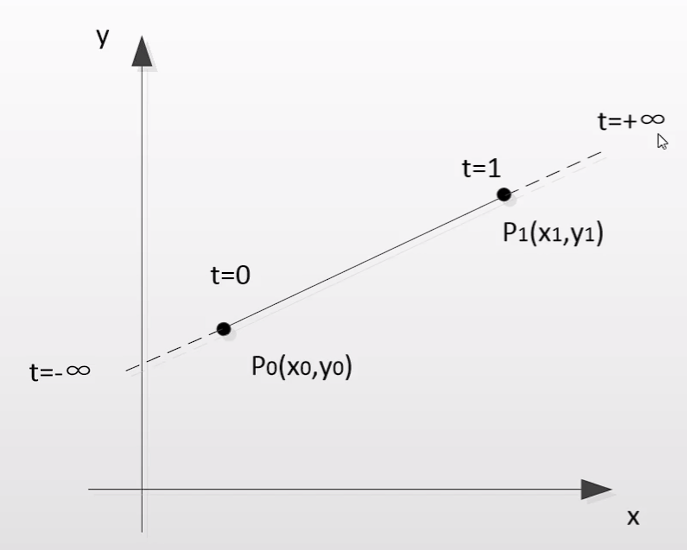
该算法是以直线的参数方程为基础设计的，把判断直线与窗口边界求交的二维裁剪问题转化为求解一组不等式，确定直线参数的一维裁剪问题。
在这里插入图片描述

当t=0的时候，是起点；当t=1的时候，是终点。
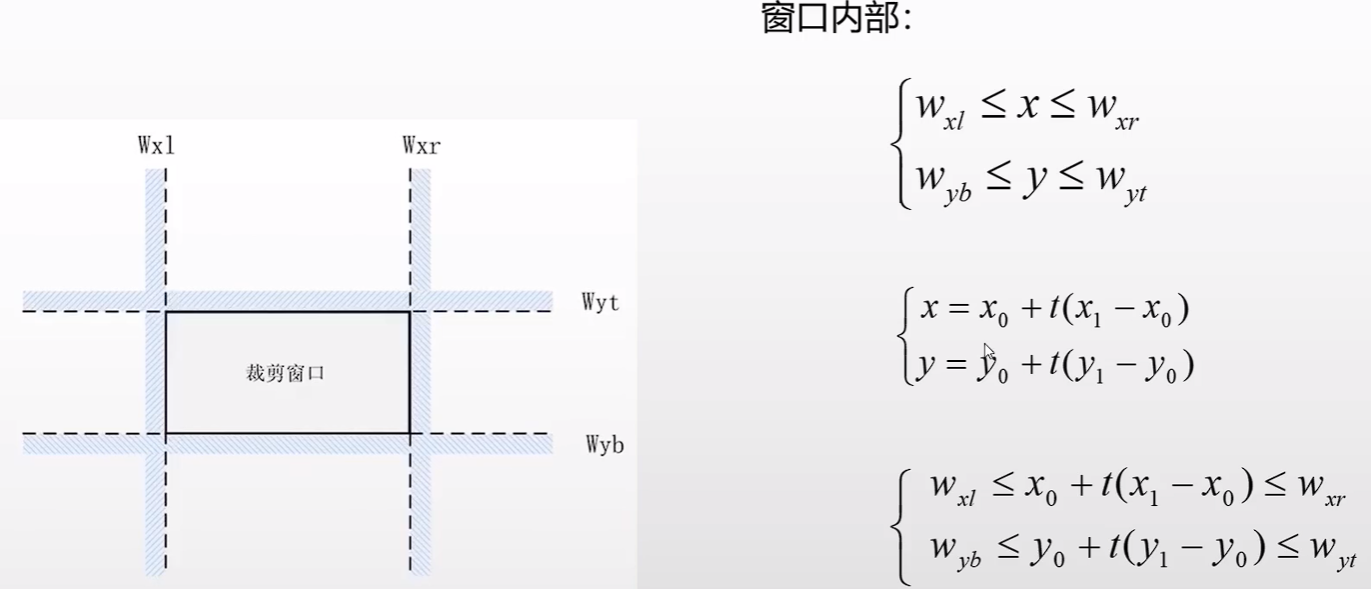
在这里插入图片描述

裁剪窗口：
在这里插入图片描述

在这里插入图片描述

这个算法主要考察参数 t 的变化。
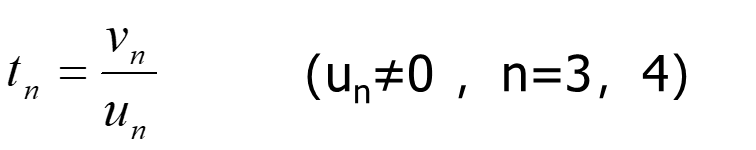
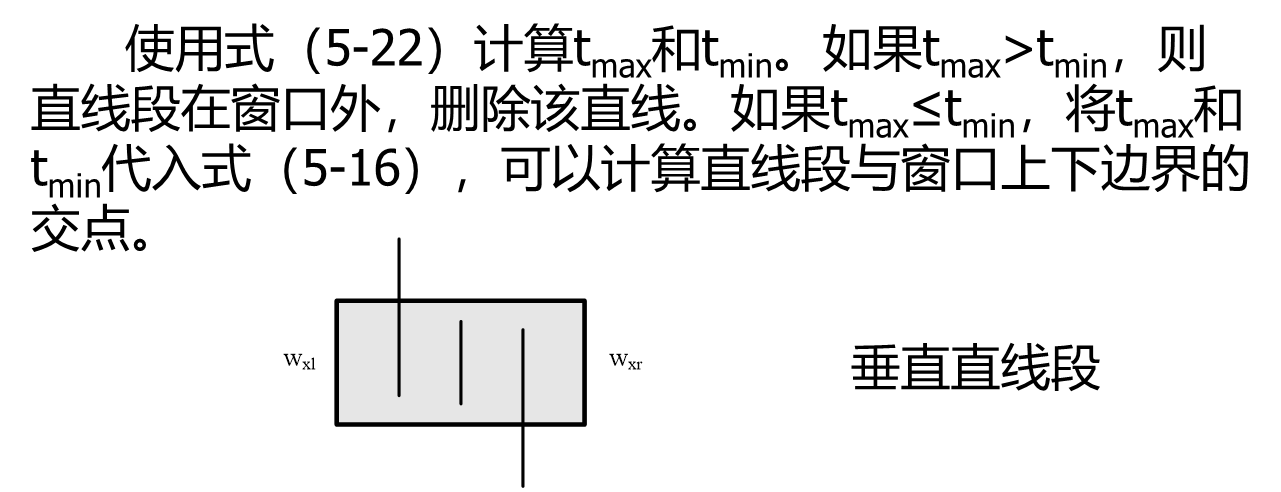
在这里插入图片描述

在这里插入图片描述

参数u的定义上边有。上图垂直的情况只需判断n=3,4 两值。

在这里插入图片描述

代码：

void CTestView::LBLineClip()//Liang-Barsky裁剪函数
{
	double tmax,tmin,dx,dy;
	dx=P[1].x-P[0].x;dy=P[1].y-P[0].y;tmax=0.0,tmin=1.0;
	if(ClipTest(-dx,P[0].x-wxl,tmax,tmin)) //窗口边界的左、右、下、上顺序裁剪直线
	{
		if(ClipTest(dx,wxr-P[0].x,tmax,tmin))
		{			
			if(ClipTest(-dy,P[0].y-wyb,tmax,tmin))
			{
				if(ClipTest(dy,wyt-P[0].y,tmax,tmin))
				{
					if(tmin<1.0)//判断直线终点
					{
						      
                                                                                            P[1].x=P[0].x+tmin*dx;
						  
                                                                                            P[1].y=P[0].y+tmin*dy
					}
					if(tmax>0.0)//判断直线的起点
					{
						 
                                                                                          P[0].x=P[0].x+tmax*dx;
						
                                                                                          P[0].y=P[0].y+tmax*dy;
					}
                  									                                }
			}
		}
	}
}

BOOL CTestView::ClipTest(double u,double v,double &tmax,double &tmin)//裁剪测试函数
{
	double t;
	BOOL ReturnValue=TRUE;
	if(u<0.0)//从裁剪窗口的外部到内部,计算起点处的tmax
	{
		t=v/u;
		if(t>tmin)
			ReturnValue=FALSE;
		else if(t>tmax)
			tmax=t;
	}
	else
	{
		if(u>0.0)//从裁剪窗口的内部到外部，计算终点处的tmin
		{
			t=v/u;
			if(t<tmax)
				ReturnValue=FALSE;
			else if(t<tmin)
				tmin=t;
		}
		else//平行于窗口边界的直线
		{
			if(v<0.0)//直线在窗口外可直接删除
				ReturnValue=FALSE;
		}
	}
	return(ReturnValue);
}

多边形裁剪算法/Sutherland-Hodgman裁剪算法

Sutherland-Hodgman裁剪算法又称为逐边裁剪算法，基本思想是用裁剪窗口的4条边依次对多边形进行裁剪。
窗口边界的裁剪顺序无关紧要，这里采用左、右、下、上的顺序。
多边形裁剪算法的输出结果为裁剪后的多边形顶点序列。
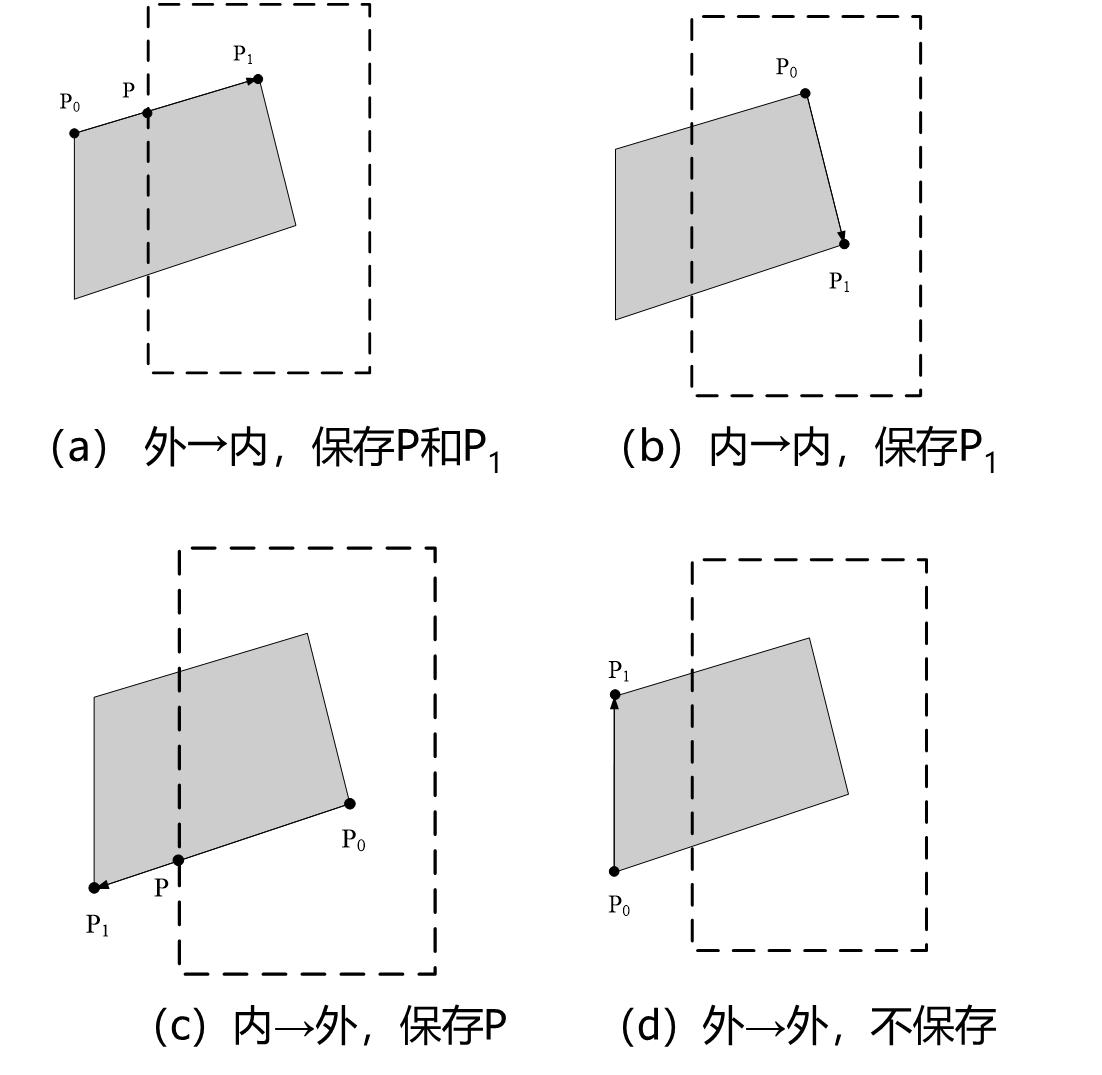
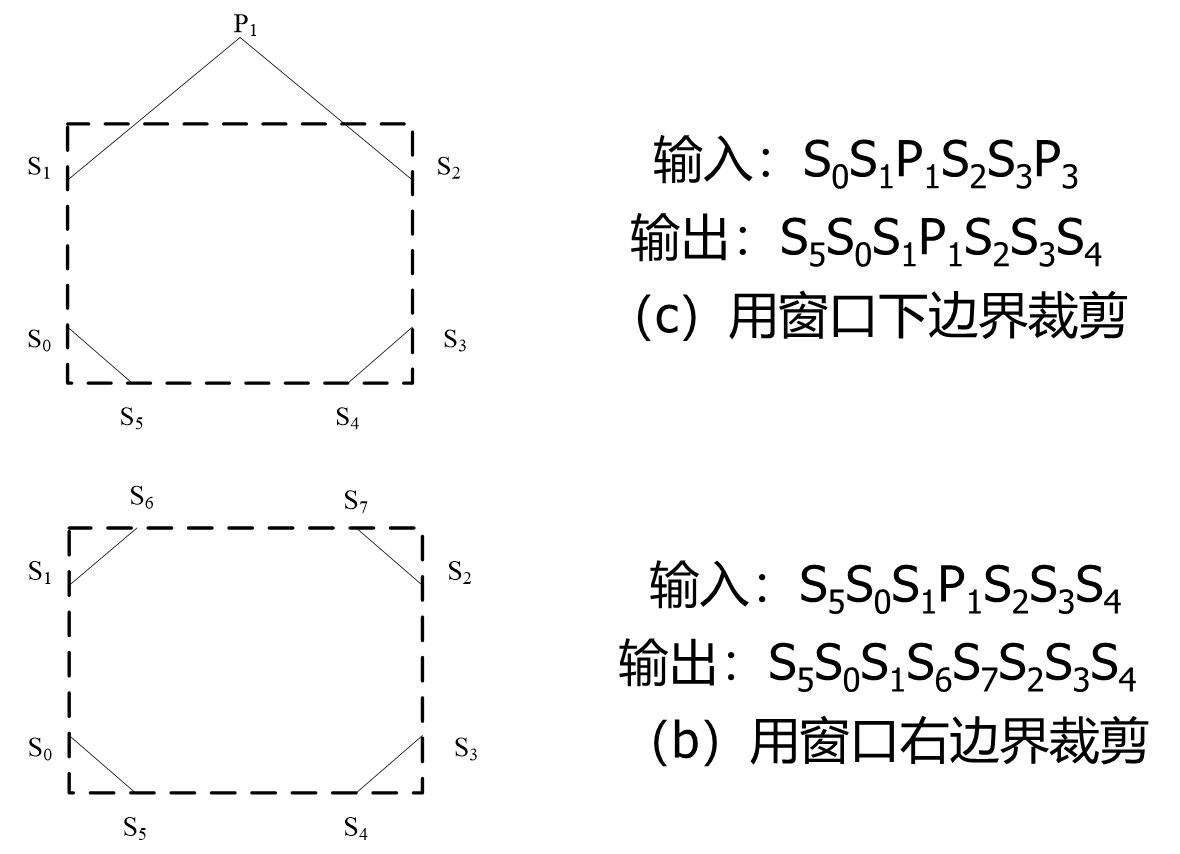
在这里插入图片描述

在这里插入图片描述

为了正确地裁剪凹多边形，一种方法是先将凹多边形分割为两个或更多的凸多边形，然后分别使用Sutherland-Hodgman裁剪算法裁剪。
另一种方法是使用Weiler-Atherton 裁剪算法。该算法适用于任何凸的、凹的带内孔的多边形裁剪，但计算工作量很大。

代码

void CTestView::ClipPolygon(CP2 *out,int Length,UINT Boundary)
{
	CP2 *pTemp=new CP2[Length];
	for(int i=0;i<Length;i++)
		pTemp[i]=out[i];
	CP2 p0,p1,p;//p0-起点，p1-终点，p-交点
	OutCount=0;
	p0=pTemp[Length-1];
	for(i=0;i<Length;i++)
	{
		p1=pTemp[i];
		if(Inside(p0,Boundary))//起点在窗口内
		{
			if(Inside(p1,Boundary))//终点在窗口内,属于内→内
			{
				Out[OutCount]=p1;//终点在窗口内
				OutCount++;
			}
			else//属于内→外
			{
				p=Intersect(p0,p1,Boundary);//求交点
				Out[OutCount]=p;
				OutCount++;
			}
		}
		
	else if(Inside(p1,Boundary))//终点在窗口内,属于外→内
		{
			p=Intersect(p0,p1,Boundary);//求交点
			Out[OutCount]=p;
			OutCount++;
			Out[OutCount]=p1;
			OutCount++;
		}
		p0=p1;
	}
	delete[] pTemp;
}