对于结点x和y,需要找他们的最近公共祖先
一个最简单的办法就是沿着x和y的父节点一个一个往上找
这样的时间复杂度是o(n),对于较大的数据量会TLE
今天要使用的方法是利用倍增来加速这个找lca的过程
倍增算法:
按2的倍数来往上找,也就是找第1,2,4,8,16,32...个父节点
而在这里,我们需要从大步往小步地去逐渐尝试
比如先尝试找第32个,不行再找第16个,以此类推
为什么不从小步往大步去尝试呢?
这和把一个十进制的数转为一个二进制的数是一样的,我们都是从最高位往最低位填1
如果填了这个1比要转换的数大了,那就不填
所以想要实现这样的算法,我们需要记录各个点的深度,以及他们距离的祖先
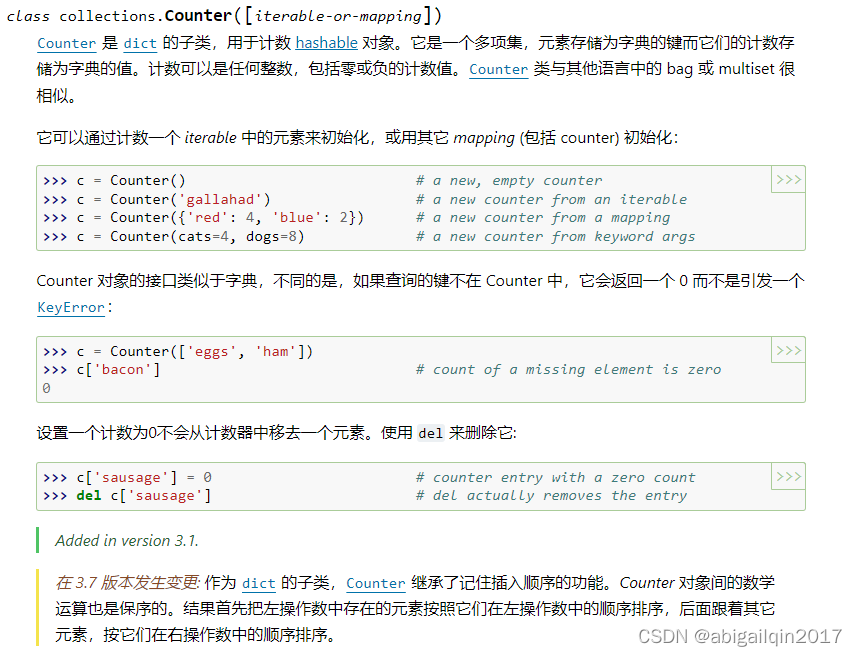
const int N=1E5;
int n,m,s;
//链式前向星
int to[N<<1],nxt[N<<1],h[N],tot;
//dep[x]记录结点x的深度
//fa[x][j]记录结点x的距离为2^j的祖先
int dep[N],fa[N][20];
//lg[i]=log2[i]+1
int lg[N];
void init(){
for(int i=1;i<=n;i++){
lg[i]=lg[i-1]+(1<<lg[i-1]==i);
}
}
//x为访问的节点
//f为x的父亲
void dfs(int x,int f){
//儿子的深度比父亲大1
dep[x]=dep[f]+1;
//节点x的距离为2^0的祖先就是自己的父亲f
fa[x][0]=f;
//更新距离x为2^i远的祖先
//由于距离2^i不可能超过dep[x],所以i只要小于lg[dep[x]]就可以了
for(int i=1;i<lg[dep[x]];i++){
//关系转移的核心公式
//距离x为2^i远的祖先就是——距离[距离x为2^(i-1)远的祖先]为2^(i-1)远的祖先
fa[x][i]=fa[fa[x][i-1]][i-1];
}
//开始遍历x的子节点
for(int i=h[x],y;y=to[i];i=nxt[i]){
//如果遍历到了自己的父亲,跳过
if(y==f) continue;
dfs(y,x);
}
}预处理完毕各个结点fa数组以后,我们就可以通过倍增算法来求得他们的lca了
在找lca的时候,可能有以下几种情况:
1.dep[x]==dep[y]
在这种情况下,我们只需要x和y同步往上爬,直到他们两个的祖先重合,就可以得到x与y的公共祖先了
2.dep[x]<dep[y]或dep[y]<dep[x]
这两种情况其实是等价的,只需要把x与y对调一下即可
现在不妨取dep[x]<dep[y]
那么这时会有两种情况:
(1) y是x的某个祖先
这个时候,x与y的lca一定是y
也就是说,只要返回y就可以了
(2)y不是x的某个祖先
这个时候,我们就应当先找到一个x的祖先,这个祖先和y的深度相同,然后再按照情况2处理
综上所述,实现代码如下:
int LCA(int x,int y){
//第1种情况
if(dep[x]<dep[y]){
swap(x, y);
}
//当x与y不处于同一个深度的时候
while(dep[x]>dep[y]){
//找到距离x为dep[x]-dep[y]的祖先
x = fa[x][lg[dep[x] - dep[y]] - 1];
}
//这个时候x和y同深度
//如果y就是x的祖先的话
//直接返回
if(x==y){
return y;
}
//如果不是的话
//共同向上爬
for (int k = lg[dep[x] - 1]; ~k;k--){
//如果向上跳到的他们的祖先不相同,说明还没有合并到同一棵子树上
//可以放心地跳到他们对应的祖先上
if(fa[x][k]!=fa[y][k]){
x = fa[x][k];
y = fa[x][k];
}
}
//循环结束以后,一定会有fa[x][0]==fa[y][0]
//这个就是他们的lca
return fa[x][0];
}