🎯要点

🎯快速傅立叶变换算法周期域解椭圆曲线波 | 🎯算法数值解孤波脉冲和结果动画 | 🎯三种语言孤子解浅水表面波方程 | 🎯渐近分解算法孤子波 | 🎯自适应步长算法孤子波 | 🎯流体自动造波器电机控制，检测孤子波碰撞 | 🎯算法计算复现无碰撞孤子波 | 🎯能量守恒定律线性隐式算法解孤波 | 🎯两种语言有限差分算法解孤波

📜孤子波用例：Python火焰锋动力学和浅水表面波浪偏微分方程

📜有限差分用例：Python微磁学磁倾斜和西塔规则算法

📜标量场用例：Python光束三维二维标量场和算法

🍇Python钢棒热微分

热方程简洁地描述了热扩散和传递的极其复杂的世界，它是一个偏微分方程，而非常微分方程，所以在求解它时，只要知道它涉及一个具有多个变量的函数的导数，而不是只有一个变量的函数。
$$\frac{\partial u}{\partial t}=k\frac{{\partial }^{2}u}{\partial x^2}$$
考虑一根初始冷的 $\left(0^{\circ }C\right)$ 金属棒，长度为 $L$，具有传递热量 $k$ 的能力。如果我们连续加热该金属棒的两端，例如 $200^{\circ }C$，那么随着时间的推移，热量将在金属棒上扩散并达到平衡。热方程告诉我们热量如何随时间传播，其解为我们提供了一个函数 $u(t,x)$，该函数可以在任何给定时间 $t$ 给出沿着杆 $x$ 的任何点的温度。

然而，与大多数微分方程一样，热方程的精确解析解极难获得，因此对于大多数应用而言，最佳解方法是我们尽可能最好的求近似值。获得这些近似值的方法有很多，但我们今天要重点讨论的是迄今为止最简单且应用最广泛的方法，即有限差分法。

假设一个未知函数 $f(x)$ 的值是我们知道的，这种情况在现实世界中与收集外部数据的任何情况下经常出现。如果我们想求 $f(x)$ 在 $n$ 点的导数，那么，我们需要找到一条与 $f(n)$​ 相切的线，并找到它的斜率，如下所示：

如果我们不知道函数 $f(x)$，则我们不可能求其导数并找到切线的斜率。而有限差分法旨在解决这个问题，它使用 $n$ 的相邻值来近似估计实际切线。如果我们查看 $n$ 之前的一个点和 $n$ 之后的一个点，并且知道它们的值，我们可以通过在 $n$ 和它的一个相邻点之间画一条线来开始估计切线。例如，我们可以尝试在 $n$ 和 $n+1$​ 之间画一条线。

$n$ 和 $n+1$ 之间的估计切线与目标切线相对相似，但让我们看看是否可以通过使用 $n$ 和 $n-1$ 来更接近。

现在我们知道如何获得估计的切线，我们现在可以使用前面提到的斜率公式来获得它的斜率，从而获得函数在该点的导数。

斜率方程：
$$\frac{y_2-y_1}{x_2-x_1}$$
我们知道 $y$ 值就是 $f(n+1)$ 和 $f(n)$​，因此代入我们所知道的斜率公式就变成：
$$\frac{f(n+1)-f(n)}{x_2-x_1}$$
$x$ 值遵循类似的套路，因为对 $x_2$ 插入 $n+1$，对 $x_1$ 插入 $n$​ 会导致：
$$\frac{f(n+1)-f(n)}{1}$$
实际上，我们的 $n$ 值很少会精确地间隔为 1，更一般的形式将使它们间隔为任意值 $dx$​，从而导致我们的有限差分导数的最终公式为：
$$\frac{df}{dx}\approx \frac{f(x+dx)-f(x)}{dx}$$
现在回到热方程，我们可以用方程的左边代替它的有限差分版本，考虑到有限微分是相对于 $t$ 发生的事实，而空间变量 $x$ 保持不变。
$$\frac{u(t+dt,x)-u(t,x)}{dt}\approx k\frac{{\partial }^{2}u}{\partial x^2}$$
在本模拟中，我们将模拟一根长度为 2 米的初始冷金属棒，两端持续加热至 200˚C，假设该棒为钢，热常数 $k$​ 为 0.466。我们将运行 10 秒的模拟，看看会发生什么。

import numpy
from matplotlib import pyplot

常量：

length = 10               
k = .466                  
temp_at_left_end = 200   
temp_at_right_end = 200   
total_time = 10           

dx = .1    
x_vec = numpy.linspace(0, length, int(length/dx))    
dt = .0001    
t_vec = numpy.linspace(0, total_time, int(total_time/dt))
u = numpy.zeros([len(t_vec), len(x_vec)])

由于我们的棒将在两端持续加热，因此我们希望棒的左侧和右侧始终分别为 temp_at_left_end 和 temp_at_right_end。从数学上讲，这可以表示为 u(t, 0) = 200 和 u(t, length) = 200（对于所有时间 t），代码如下：

u[:, 0] = temp_at_left_end     
u[:, -1] = temp_at_right_end  

您可以看到两端的温度很高，而其他地方的温度均为 0，因此，我们准备解决这个问题！我们要做的就是迭代沿棒的所有点和所有时间点，将它们代入我们之前推导的方程中。

for t in range(1, len(t_vec)-1):
    for x in range(1, len(x_vec)-1):
        u[t+1, x] = k * (dt / dx**2) * (u[t, x+1] - 2*u[t, x] + 
                    u[t, x-1]) + u[t, x]

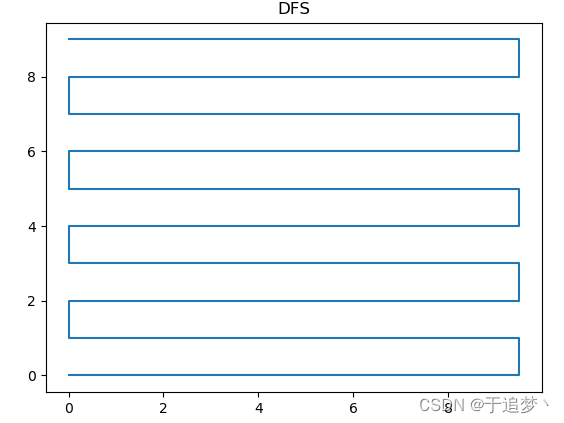
要可视化它，只需在循环内部调用 pyplot.plot() 即可获得动画绘图，或在循环外部调用 pyplot.plot() 获得静态绘图。

参阅：👉 计算思维 | 亚图跨际