gici-open学习日记(7)：GNSS图优化—

gici-open学习日记——GNSS RTK图优化

前言
初始化RTK的调用
`rearrangePhasesAndCodes`
双差构造`formPhaserangeDDPair`
周跳探测`cycleSlipDetectionSD`
添加参数块
- 模糊度参数部分`addSdAmbiguityParameterBlocks`
- 添加双差伪距残差`addDdPseudorangeResidualBlocks`
- 添加双差相位残差`addDdPhaserangeResidualBlocks`
- 添加多普勒观测残差`addDopplerResidualBlocks`
- 其他一些参数块的添加
伪距双差残差`PseudorangeErrorDD`
- `EvaluateWithMinimalJacobians`
相位双差残差`PseudorangeErrorDD`
- `EvaluateWithMinimalJacobians`
多普勒残差`DopplerError`
- `EvaluateWithMinimalJacobians`
添加相对残差
更新DOP值`updateGdop`

前言

自己其实很久没有看这个框架了，包括后续代码好像也更新了不少，不过正好过一阵可能就要准备找工作了，这里就当简单把RTK的知识稍微看一下吧。如果和最新版本的代码有冲突的地方还请以最新版本为主

初始化RTK的调用

这个的调用流程和SPP是一样的，只不过相当于是在SPP调用的上一层，具体在GnssImuInitializer::addMeasurement函数里

bool GnssImuInitializer::addMeasurement(const EstimatorDataCluster& measurement)
{
    /* 这部分不关注的代码 */
    if (sub_gnss_estimator_->addMeasurement(*measurement.gnss)) {
    /* 这部分不关注的代码 */
}

事实上，在进行具体的RTK解算之前，需要进行SPP提供给RTK解算的初值，所以才会在RtkEstimator::addGnssMeasurementAndState函数的最前面先进行SPP观测的添加以及SPP的解算

关于RtkEstimator::addGnssMeasurementAndState这个函数，大概的流程在gici-open学习日记(5)：runMeasurementAddin函数引申——初始化这篇文章的“GNSS/INS初始化补充1：RtkEstimator流程”这里梳理过，所以这里不再梳理具体的流程，重点关注具体的参数块添加和解算

`rearrangePhasesAndCodes`

我的理解是这个函数是删除重复的相位，让每个观测值只对应一个相位的函数。这里面的核心是把载波相位和期对应的伪距码对应起来，如果不对应的情况，就把伪距观测值根据不同的DCB对应到同一个基础下，我在原函数的基础上加了一点点注释，就不特别详细地展开记录了。

void rearrangePhasesAndCodes(GnssMeasurement& measurement, bool accept_coarse)
{
  CodeBiasPtr code_bias = measurement.code_bias;
  for (auto& sat : measurement.satellites) {
    std::string prn = sat.first;
    char system = prn[0];
    Satellite& satellite = sat.second;
    std::unordered_map<int, Observation>& observations = satellite.observations;
    std::unordered_map<int, Observation> arranged_observations;   // 重新排序的观测
    for (auto it = observations.begin(); it != observations.end(); it++) {
      std::pair<int, Observation> arranged_observation;
      int code = it->first;
      Observation observation = it->second;
      int phase_id = getPhaseID(system, code);
      int default_code = 0;
#define MAP(S, P, C) \
  if (system == S && phase_id == P) { default_code = C; }
  PHASE_CHANNEL_TO_DEFAULT_CODE;  // 为每个载波相位分配默认的码
#undef MAP
      bool can_add = true;
      // do not need to arrange
      if (default_code == code) arranged_observation = *it;
      // arrange to default code
      else {
        double bias = code_bias->getCodeBias(prn, code, accept_coarse);
        double default_bias = 
          code_bias->getCodeBias(prn, default_code, accept_coarse);
        // do not have code bias
        if (bias == 0.0 || default_code == 0.0) {
          // consider DCBs in the same frequency are zeros
          if (accept_coarse) {
            arranged_observation = std::make_pair(default_code, observation);
          } 
          // cannot arrange
          else {
            // pass
            can_add = false;
          }
        }
        // use code bias to arrange
        else {
          observation.pseudorange += bias - default_bias; // 相当于把伪距观测值也对齐到默认码下面
          arranged_observation = std::make_pair(default_code, observation);
        }
      }
      // add to observations
      if (can_add) {
        if (arranged_observations.find(default_code) == arranged_observations.end()) {
          arranged_observations.insert(arranged_observation);
        }
      }
    }
    satellite.observations = arranged_observations;
  }
}

双差构造`formPhaserangeDDPair`

双差的公式manual里有给出了，这里不再详细记录
在这里插入图片描述
formPhaserangeDDPair进行了观测值双差的构建，其调用的参数有三个

const GnssMeasurement& measurement_rov, 	// 流动站观测值
const GnssMeasurement& measurement_ref,		// 基准站观测值
const GnssCommonOptions& options			// GNSS基本的配置选项

函数先对接收机之间做了一次单差

  GnssMeasurementSDIndexPairs sd_pairs = formPhaserangeSDPair(
    measurement_rov, measurement_ref, options); // 先对接收机间做一个单差

接下来先定义了5个变量，不过有一个目前来看是没有用到的。代码的话就是针对每一个变量进行赋值

   /**
   * prn_to_number_phases 卫星和载波相位数对应起来
   * prn_to_index         每一个卫星prn所对应的在单差sd_pairs的索引
   * prn_to_phases        prn和载波相位对应起来
   * system_to_num_phases 卫星系统和载波相位的对应，每一种系统挑出载波观测最多的以可卫星      
   */
  std::map<char, int> system_to_num_phases;
  std::multimap<char, double> system_to_phases; // FIXME 没用到
  std::map<std::string, int> prn_to_number_phases;
  std::multimap<std::string, double> prn_to_phases;
  std::multimap<std::string, int> prn_to_indexes;

然后// Find base satellites for each system and phases，这里就是为形成双差挑选一颗基础卫星，操作和RTKLIB是一样的，也是找出卫星高度角最大的。

  std::map<char, std::string> system_to_base_prn;
  for (size_t i = 0; i < getGnssSystemList().size(); i++) {
    char system = getGnssSystemList()[i];

    double max_elevation = 0.0;
    for (size_t j = 0; j < sd_pairs.size(); j++) {
      if (sd_pairs[j].rov.prn[0] != system) continue;

      // we only select satellites with max phase number
      if (prn_to_number_phases.at(sd_pairs[j].rov.prn) != 
          system_to_num_phases.at(system)) continue;

      double elevation = satelliteElevation(  // 相对参考站的卫星高度角
        measurement_ref.getSat(sd_pairs[j].ref).sat_position, 
        measurement_ref.position);
      if (max_elevation < elevation) {
        system_to_base_prn[system] = sd_pairs[j].rov.prn;
        max_elevation = elevation;          // 找到最大的卫星高度角
      }
    }
  }

最后就是形成双差了，这里也是只是形成了双差的结构，但没有完成具体的双差计算

  GnssMeasurementDDIndexPairs dd_pairs;
  for (size_t i = 0; i < sd_pairs.size(); i++) {
    char system = sd_pairs[i].rov.prn[0]; 
    std::string prn = sd_pairs[i].rov.prn;
    std::string prn_base = system_to_base_prn.at(system);

    if (prn == prn_base) continue;  // 同一颗卫星无法形成双差

    for (auto it = prn_to_indexes.lower_bound(prn_base); 
         it != prn_to_indexes.upper_bound(prn_base); it++) {
      GnssMeasurementSDIndexPair& sd_pair_base = sd_pairs[it->second];
      int phase_id_base = getPhaseID(system, sd_pair_base.rov.code_type);
      int phase_id = getPhaseID(system, sd_pairs[i].rov.code_type);
      if (phase_id_base == phase_id) {
        dd_pairs.push_back(GnssMeasurementDDIndexPair(  // 形成了双差结构
          sd_pairs[i].rov, sd_pairs[i].ref, sd_pair_base.rov, sd_pair_base.ref));
        break;
      }
    }
  }

周跳探测`cycleSlipDetectionSD`

周跳的精确探测可以确保正确的模糊度参数化，包括整周模糊度的搜索准则，所以也是RTK解算的一个重要部分。

GICI和RTKLIB一样，也是在一上来利用LLI对周跳进行探测。LLI（Loss of Lock Indicator）表示失锁标识符，和接收机板卡的性能有关系。但在实际GNSS处理中，有些板卡也会把不是周跳通过LLI探测成周跳，周跳的过探测对后边的固定率影响也比较大，所以这个选项是可以根据自己的需要进行修改的，不过那都是很特殊的需求了。

  cycleSlipDetectionLLI(measurement_rov_pre, measurement_rov_cur);
  cycleSlipDetectionLLI(measurement_ref_pre, measurement_ref_cur);

关于cycleSlipDetectionLLI函数，就是根据当前历元的LLI标志和上一历元LLI与当前历元LLI是否一致判断的。

void cycleSlipDetectionLLI(GnssMeasurement& measurement_pre, 
                           GnssMeasurement& measurement_cur)
{
  for (auto& sat : measurement_cur.satellites) {  // 先根据当前历元的LLI判断有没有周跳
    for (auto& obs : sat.second.observations) {
      Observation& observation = obs.second;
      if (observation.LLI & 1) {
        observation.slip = true;
        continue;
      }

      // detect slip by parity unknown flag transition in LLI
      uint8_t LLI_cur = observation.LLI;          // 再根据两个历元的LLI是否一样判断
      auto it_sat = measurement_pre.satellites.find(sat.first);
      if (it_sat == measurement_pre.satellites.end()) continue;
      auto it_obs = it_sat->second.observations.find(obs.first);
      if (it_obs == it_sat->second.observations.end()) continue;
      uint8_t LLI_pre = it_obs->second.LLI;
      if (((LLI_pre & 2) && !(LLI_cur & 2)) || (!(LLI_pre & 2) && (LLI_cur & 2))) {
        observation.slip = true;
#if LOG_CYCLE_SLIP
        LOG(INFO) << "Detected cycle slip by LLI at " << sat.second.prn << ".";
#endif
      }
    }
  }
}

接下来分别生成了上一历元与当前历元的单差观测值，这里不仅构造了GnssMeasurementSDIndexPairs单差类型的变量，还完成了具体单差观测值的计算。
然后根据GF组合进行了周跳探测

Under not disturbed ionospheric conditions, the geometry-free combination performs as a very precise and smooth test signal,
driven by the ionospheric refraction. Although, for instance, the jump produced by a simultaneous one-cycle slip in both signals is smaller in this combination than in the original signals (λ2-λ1 =5.4cm), it can provide reliable detection even for small jumps

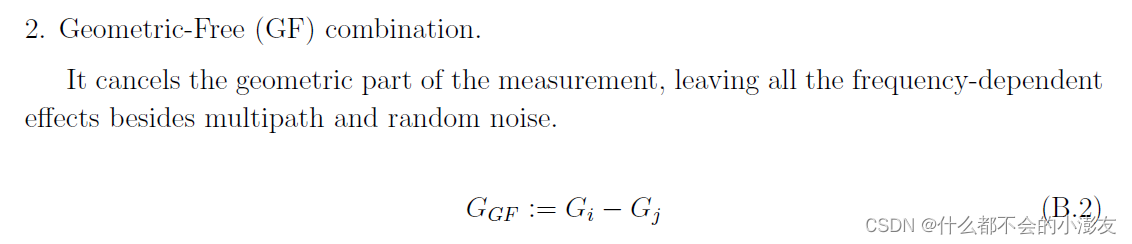
在这里插入图片描述
代码也很简单，就是分别计算得到了上一历元和当前历元的GF值，然后作差和阈值比较，大于阈值就认为发生了周跳。具体的计算内容在

cycleSlipDetectionGF(measurement_sd_pre, measurement_sd_cur, options.gf_sd_slip_thres);

根据时间间隔判断是否周跳
这个的核心就在于cycleSlipDetectionTimeGap中的一行代码

cycleSlipDetectionTimeGap(measurement_sd_pre, measurement_sd_cur, options.period * 1.5);

// cycleSlipDetectionTimeGap函数中
if (measurement_cur.timestamp - measurement_pre.timestamp < max_time_gap) {
    return;
  }

如果时间间隔大于设置的阈值，然后接下来又在代码中判断确认是单频率，就直接认为发生了周跳

最后就是周跳的汇总了，当流动站和参考站中有一个发生周跳的时候，就会认为当前的历元发生了周跳

  for (size_t i = 0; i < pairs_cur.size(); i++) {
    Observation& observation_sd = measurement_sd_cur.getObs(pairs_cur[i].rov);
    Observation& observation_rov = measurement_rov_cur.getObs(pairs_cur[i].rov);
    Observation& observation_ref = measurement_ref_cur.getObs(pairs_cur[i].ref);
    observation_rov.slip |= observation_sd.slip;
    observation_ref.slip |= observation_sd.slip;
  }

添加参数块

模糊度参数部分`addSdAmbiguityParameterBlocks`

  addSdAmbiguityParameterBlocks(curGnssRov(), 
    curGnssRef(), index_pairs, curGnssRov().id, curAmbiguityState());

前几个参数很好理解，就是当前的流动站、基准站、双差以及ID，最后一个参数得到的是模糊度状态容器ambiguity_states_(定义在gnss_estimator_base.h里)的最后一个变量，这里只是加入到参数块之中，具体的解算也在后面

函数上来先利用之前形成的双差关系得到了一些变量，在后边可能会用到

const Satellite& satellite = // 先利用双差得到了一些之后可能会用的变量
      measurement_rov.getSat(index_pair.rov);
// 。。。这里省略了一些变量

然后根据ID判断在图优化中是否已经存在了

    double code = index_pair.rov.code_type;
    double wavelength = observation.wavelength; // FIXME 没用到啊
    double phase_id = gnss_common::getPhaseID(system, code);
    BackendId ambiguity_id = createGnssAmbiguityId(satellite.prn, phase_id, id);
    CHECK(!graph_->parameterBlockExists(ambiguity_id.asInteger())) 
      << "Ambiguity parameter for " << satellite.prn << " in phase " 
      << phase_id << " has already been added!";

接下来用伪距和载波相位观测值给了个初值，其实原理就是用两个观测方程减一下就得到了

TODO：事实上前面定义了波长的变量，按理说这里给初值用这个变量好一点，不过这里没有用到。我觉得用一下是不是比较好？

    double phaserange = observation.phaserange; // 这里利用伪距和载波观测给了个初值
    double pseudorange = observation.pseudorange;
    double phaserange_ref = observation_ref.phaserange;
    double pseudorange_ref = observation_ref.pseudorange;
    double ambiguity = phaserange - phaserange_ref -
                      (pseudorange - pseudorange_ref);
    // TODO ambiguity /= wavelength;

接下来就是构建模糊度参数并加到图中了

    Eigen::Matrix<double, 1, 1> init;
    init[0] = ambiguity;
    std::shared_ptr<AmbiguityParameterBlock> ambiguity_parameter_block = 
      std::make_shared<AmbiguityParameterBlock>(init, ambiguity_id.asInteger());
    CHECK(graph_->addParameterBlock(ambiguity_parameter_block));
    state.ids.push_back(ambiguity_id);

因为形成双差是需要一颗base_satellite的，所以接下来就是对这个卫星再进行一遍类似的操作

    BackendId ambiguity_base_id =   // 这里为作为基础的那颗卫星添加参数块
      createGnssAmbiguityId(satellite_base.prn, phase_id, id);
    if (!graph_->parameterBlockExists(ambiguity_base_id.asInteger())) 
    {
      phaserange = observation_base.phaserange;
      pseudorange = observation_base.pseudorange;
      phaserange_ref = observation_ref_base.phaserange;
      pseudorange_ref = observation_ref_base.pseudorange;
      ambiguity = phaserange - phaserange_ref - 
                        (pseudorange - pseudorange_ref);
      // TODO 同理，这里是不是也可以利用上波长信息作为初值？
      /**
       * wavelength = observation_base.wavelength;
       * ambiguity /= wavelength;
        */
      Eigen::Matrix<double, 1, 1> init_base;
      init_base[0] = ambiguity;
      std::shared_ptr<AmbiguityParameterBlock> ambiguity_base_parameter_block = 
        std::make_shared<AmbiguityParameterBlock>(
          init_base, ambiguity_base_id.asInteger());
      CHECK(graph_->addParameterBlock(ambiguity_base_parameter_block));
      state.ids.push_back(ambiguity_base_id);

最后添加模糊度的残差

      addAmbiguityResidualBlock(ambiguity_base_id, init_base[0], 	// 在构建误差的时候会执行setInformation的操作
        gnss_base_options_.error_parameter.initial_ambiguity);

添加双差伪距残差`addDdPseudorangeResidualBlocks`

这个函数也是进行了参数块的添加，关于参数块的核心计算步骤不在这个函数里，也是分为了ECEF和ENU两种框架下

// 这里用ENU框架下的代码举例子
      else {
        is_state_pose_ = true;  // ENU框架下
        BackendId pose_id = state.id_in_graph;
        std::shared_ptr<PseudorangeErrorDD<7, 3>> pseudorange_error = 
          std::make_shared<PseudorangeErrorDD<7, 3>>( // 主要是进行构建这个残差
          measurement_rov, measurement_ref, 
          index_pair.rov, index_pair.ref, index_pair.rov_base, index_pair.ref_base,
          gnss_base_options_.error_parameter); 
        pseudorange_error->setCoordinate(coordinate_);
        graph_->addResidualBlock(pseudorange_error, 
          huber_loss_function_ ? huber_loss_function_.get() : nullptr,
          graph_->parameterBlockPtr(pose_id.asInteger()), 
          graph_->parameterBlockPtr(gnss_extrinsics_id_.asInteger()));
      }

添加双差相位残差`addDdPhaserangeResidualBlocks`

这个和上一个函数没啥区别，不过是相位观测的话残差的维度会变多(模糊度)，这里就不再重复记录了

  // Add phaserange residual blocks
  addDdPhaserangeResidualBlocks(curGnssRov(), curGnssRef(), index_pairs, curState()); // 相位双差残差

添加多普勒观测残差`addDopplerResidualBlocks`

这个其实和前两个也没什么不同，不过就是添加进去的残差信息换成多普勒观测量的了，关于多普勒的残差因子可以看manual的3.4.3节，这里代码也没有什么特别的东西，不再重复记录

  if (rtk_options_.estimate_velocity) {
    addDopplerResidualBlocks(curGnssRov(), curState(), num_valid_satellite);          // 多普勒残差
  }

其他一些参数块的添加

其实剩下添加的一些残差块都差不多，核心都在于残差构建的地方，那就不在具体的添加残差的函数里了，所以这里就不一一详细记录了，只是大概列一下都加了哪些

  if (!isFirstEpoch()) {
    if (!rtk_options_.estimate_velocity) {
      // position
      addRelativePositionResidualBlock(lastState(), curState());    // 相对位置残差
    }
    else {
      // position and velocity
      addRelativePositionAndVelocityBlock(lastState(), curState()); // 速度和位置
      // frequency
      addRelativeFrequencyBlock(lastState(), curState());           // 频率
    }
    // ambiguity
    addRelativeAmbiguityResidualBlock(                              // 模糊度残差
      lastGnssRov(), curGnssRov(), lastAmbiguityState(), curAmbiguityState());
  }

伪距双差残差`PseudorangeErrorDD`

关于双差伪距残差的几种形式，注释里也给出了比较详细的解释

// Group 1: P1. receiver position in ECEF (3)
// Group 2: P1. body pose in ENU (7), P2. relative position from body to receiver
// in body frame (3)
// Group 3: Group 1 + P2. troposphere delay at rov (1), P3. troposphere delay at ref (1)
// P4. ionosphere delay (1), P5. ionosphere delay of base satellite (1)
// Group 4: Group 2 + P3. troposphere delay at rov (1), P4. troposphere delay at ref (1),
// P5. ionosphere delay (1), P6. ionosphere delay of base satellite (1)

构造函数也是判断了具体是哪种形式，以及调用setInfoemation设置了信息矩阵

`EvaluateWithMinimalJacobians`

残差和雅可比矩阵的计算在这个函数里

首先是得到了在ECEF下的坐标

  if (!is_estimate_body_)   // ECEF框架下
  {
    t_WR_ECEF = Eigen::Map<const Eigen::Vector3d>(parameters[0]);
  }
  else 
  {
    // pose in ENU frame
    t_WS_W = Eigen::Map<const Eigen::Vector3d>(&parameters[0][0]);
    q_WS = Eigen::Map<const Eigen::Quaterniond>(&parameters[0][3]);

    // relative position
    t_SR_S = Eigen::Map<const Eigen::Vector3d>(parameters[1]);

    // receiver position
    Eigen::Vector3d t_WR_W = t_WS_W + q_WS * t_SR_S;

    if (!coordinate_) {
      LOG(FATAL) << "Coordinate not set!";
    }
    if (!coordinate_->isZeroSetted()) {
      LOG(FATAL) << "Coordinate zero not set!";
    }
    t_WR_ECEF = coordinate_->convert(t_WR_W, GeoType::ENU, GeoType::ECEF);
  }

然后计算了卫星到接收机的距离，因为是双差所以也是分为base satellite和使用到的另一颗

  double rho_rov = gnss_common::satelliteToReceiverDistance(  // 接收机和卫星的距离
    satellite_rov_.sat_position, t_WR_ECEF);
  double rho_ref = gnss_common::satelliteToReceiverDistance(
    satellite_ref_.sat_position, measurement_ref_.position);
  double rho_rov_base = gnss_common::satelliteToReceiverDistance( // 接收机和base卫星的距离
    satellite_rov_base_.sat_position, t_WR_ECEF);
  double rho_ref_base = gnss_common::satelliteToReceiverDistance(
    satellite_ref_base_.sat_position, measurement_ref_.position);

然后和距离一样，计算对应的高度角

  double elevation_rov = gnss_common::satelliteElevation(
    satellite_rov_.sat_position, t_WR_ECEF);
  double elevation_ref = gnss_common::satelliteElevation(
    satellite_ref_.sat_position, measurement_ref_.position);
  double elevation_rov_base = gnss_common::satelliteElevation(
    satellite_rov_base_.sat_position, t_WR_ECEF);
  double elevation_ref_base = gnss_common::satelliteElevation(
    satellite_ref_base_.sat_position, measurement_ref_.position);

在短基线的情况下，认为大气延迟都被双差模型消除了，就不再计算大气相关的延迟量了；而如果选择估计大气延迟，就要计算对应的延迟量

  if (!is_estimate_atmosphere_) 
  {
    // We think all atmosphere delays are eliminated by double-difference
  }
  else
  { 
    // use estimated atomspheric delays
    double zwd_rov = 0.0, zwd_ref = 0.0;
    double dionosphere_delay_cur = 0.0, dionosphere_delay_base = 0.0;
    if (!is_estimate_body_) {
      zwd_rov = parameters[1][0];
      zwd_ref = parameters[2][0];
      dionosphere_delay_cur = parameters[3][0];
      dionosphere_delay_base = parameters[4][0];
    }
    else {
      zwd_rov = parameters[2][0];
      zwd_ref = parameters[3][0];
      dionosphere_delay_cur = parameters[4][0];
      dionosphere_delay_base = parameters[5][0];
    }

    // troposphere hydro-static delay
    double zhd_rov = gnss_common::troposphereSaastamoinen(
      timestamp, t_WR_ECEF, PI / 2.0);
    double zhd_ref = gnss_common::troposphereSaastamoinen(
      timestamp, t_WR_ECEF, PI / 2.0);
    double zhd_rov_base = gnss_common::troposphereSaastamoinen(
      timestamp, t_WR_ECEF, PI / 2.0);
    double zhd_ref_base = gnss_common::troposphereSaastamoinen(
      timestamp, t_WR_ECEF, PI / 2.0);
    // mapping
    gnss_common::troposphereGMF(  // 投影函数模型
      timestamp, t_WR_ECEF, elevation_rov, &gmf_hydro_rov, &gmf_wet_rov);
    gnss_common::troposphereGMF(
      timestamp, t_WR_ECEF, elevation_ref, &gmf_hydro_ref, &gmf_wet_ref);
    gnss_common::troposphereGMF(
      timestamp, t_WR_ECEF, elevation_rov_base, &gmf_hydro_rov_base, &gmf_wet_rov_base);
    gnss_common::troposphereGMF(
      timestamp, t_WR_ECEF, elevation_ref_base, &gmf_hydro_ref_base, &gmf_wet_ref_base);
    dtroposphere_delay = zhd_rov * gmf_hydro_rov - zhd_ref * gmf_hydro_ref - 
      zhd_rov_base * gmf_hydro_rov_base + zhd_ref_base * gmf_hydro_ref_base + 
      zwd_rov * gmf_wet_rov - zwd_ref * gmf_wet_ref - 
      zwd_rov * gmf_wet_rov_base + zwd_ref * gmf_wet_ref_base;

    // ionosphere 
    dionosphere_delay_cur = gnss_common::ionosphereConvertFromBase(
      dionosphere_delay_cur, observation_rov_.wavelength);
    dionosphere_delay_base = gnss_common::ionosphereConvertFromBase(
      dionosphere_delay_base, observation_rov_base_.wavelength);
    dionosphere_delay = dionosphere_delay_cur - dionosphere_delay_base;
  }

接下来就是计算残差以及赋权了

  double dpseudorange_estimate = rho_rov - rho_ref - rho_rov_base + rho_ref_base
 + dtroposphere_delay + dionosphere_delay;

  // Compute error
  double dpseudorange = observation_rov_.pseudorange - observation_ref_.pseudorange -
    observation_rov_base_.pseudorange + observation_ref_base_.pseudorange;
  Eigen::Matrix<double, 1, 1> error = 
    Eigen::Matrix<double, 1, 1>(dpseudorange - dpseudorange_estimate);
    
  Eigen::Map<Eigen::Matrix<double, 1, 1> > weighted_error(residuals);
  weighted_error = square_root_information_ * error;  // 利用在构造函数中得到的权重进行赋权的操作

计算雅可比矩阵，对应着manual的3.8.3节中的第一个残差，具体的雅可比计算在3.4.1节中的Formulation 11形式里，待估参数形式：

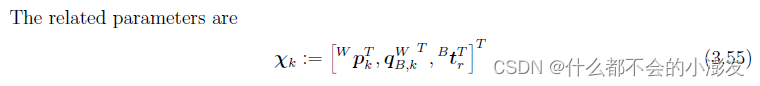
残差形式：

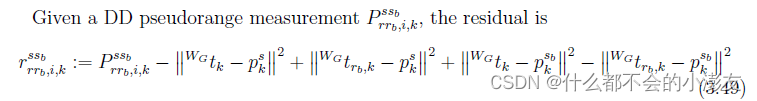
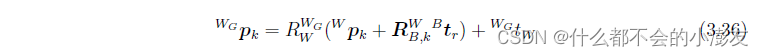
在这里插入图片描述

雅可比的形式：
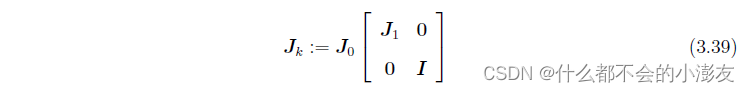
具体的J0以及J1：

在这里插入图片描述

相位双差残差`PseudorangeErrorDD`

相位双差主要比伪距残差多了一维模糊度的参数，但是具体形式的分类和伪距是一样的，也是根据是否估计大气延迟进行分类的。在具体的构造函数中，选择了残差的形式并利用setInfomation设置了信息矩阵以及对应的权重。

`EvaluateWithMinimalJacobians`

这里和伪距残差的部分也没什么不同，多的模糊度的部分雅可比对应到manual里的公式(3.80)又是-1和1
在这里插入图片描述

    Eigen::Matrix<double, 1, 1> J_amb = -Eigen::MatrixXd::Identity(1, 1); // 模糊度对应的雅可比部分
    Eigen::Matrix<double, 1, 1> J_amb_base = Eigen::MatrixXd::Identity(1, 1);

剩下的和伪距残差没有特别大的区别，对应3.8.3中的第二个残差，具体可以参考manual的3.4.2小节，这里就不再详细记录了

多普勒残差`DopplerError`

如果需要对速度进行估计的情况下就会用到多普勒观测量，这个时候也就需要计算对应的多普勒残差。多普勒的残差只根据框架分为了ECEF框架下和ENU框架下两种形式，构造函数则是可以选择是否设置角速度的值，如果选择设置角度速的值，就会在执行完正常的构造函数后再给角速度赋值

template<int... Ns>
DopplerError<Ns ...>::DopplerError(
                       const GnssMeasurement& measurement,
                       const GnssMeasurementIndex index,
                       const GnssErrorParameter& error_parameter,
                       const Eigen::Vector3d& angular_velocity)
  : DopplerError(measurement, index, error_parameter)
{
  angular_velocity_ = angular_velocity;
}

关于具体调用哪种形式，也是根据框架来的，如果是ECEF框架下就不会设置，反之就会设置这个值

// gnss_estimator_base.cpp
      if (parameter_id.type() == IdType::gPosition) {
        /* 无关的代码 */
        std::shared_ptr<DopplerError<3, 3, 1>> doppler_error = 
          std::make_shared<DopplerError<3, 3, 1>>(measurement, 
          GnssMeasurementIndex(satellite.prn, obs.first), 
          gnss_base_options_.error_parameter);
        /* 无关的代码 */
      }
      // pose in ENU for fusion
      else {
        /* 无关的代码 */
        std::shared_ptr<DopplerError<7, 9, 3, 1>> doppler_error = 
          std::make_shared<DopplerError<7, 9, 3, 1>>(measurement, 
          GnssMeasurementIndex(satellite.prn, obs.first), 
          gnss_base_options_.error_parameter, angular_velocity);
        /* 无关的代码 */
      }

`EvaluateWithMinimalJacobians`

残差和雅可比的计算也是对照着手册来就可以了，对应着manual残差中的第三部分，具体到3.4.3小节，在ENU融合框架的形式下：

待估参数的形式为：
残差的计算：
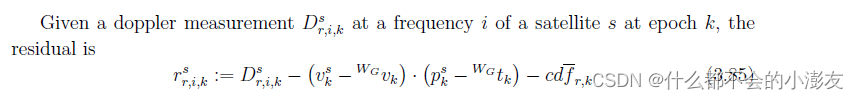
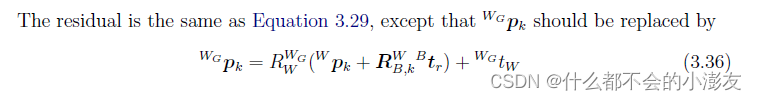
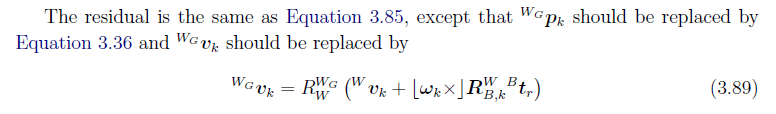
具体的雅可比计算

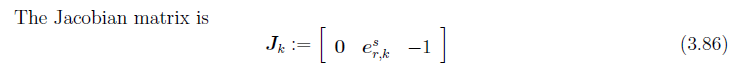
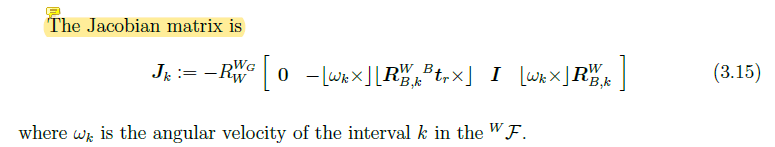
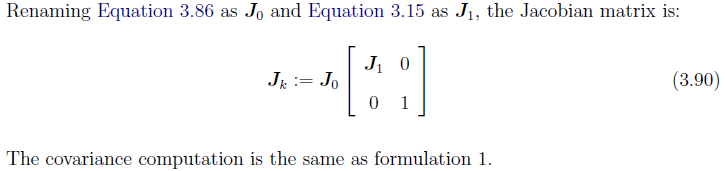
添加相对残差

相对残差的概念在manual 3.7.3有介绍
在这里插入图片描述
关于这部分的代码可以在RelativeConstError和RelativeIntegrationError找到，比如对应到公式(3.136)的这个

  RelativeIntegrationError(const Eigen::Matrix<double, Dim, Dim>& psd, double dt) { // 设置权阵
    Eigen::MatrixXd covariance = Eigen::MatrixXd::Zero(2*Dim, 2*Dim);
    covariance.topLeftCorner(Dim, Dim) = psd * pow(dt, 3) / 3.0;
    covariance.topRightCorner(Dim, Dim) = psd * pow(dt, 2) / 2.0;
    covariance.bottomLeftCorner(Dim, Dim) = psd * pow(dt, 2) / 2.0;
    covariance.bottomRightCorner(Dim, Dim) = psd * dt;
    setCovariance(covariance);
    dt_ = dt;
  }

更新DOP值`updateGdop`

DOP (dilution of precision)值，代表着精度因子，是用来判断卫星相对于观测者的几何位置所造成误差（卫星几何效应）的单位，会随卫星和接受器间的相对移动而变化，通常值越低代表误差越小。在GICI中，DOP值的计算是在函数gnss_common::computeDops中

  inline void updateGdop(
    const GnssMeasurement& measurement_rov, const GnssMeasurementDDIndexPairs& indexes) {
    gdop_ = gnss_common::computeDops(
      measurement_rov, indexes, gnss_base_options_.common).x();
  }

这个函数核心的计算部分是调用了RTKLIB的dops函数

dops(ns, azel, degreeToRad(options.min_elevation), Dops.data());

关于这部分的原理，其实很简单，就只是一种精度的评价方式
在这里插入图片描述