前言
在前端开发过程中,关于算法的使用也是非常常见的操作,尤其是处理一些复杂的业务场景,还有就是前端获取到后端返回的复杂结构的数据,所以说前端开发中处处都有算法使用的场景。开发者从接触编程开发开始,就与算法脱不了干系了,算法又和数学分不开,总归到底还是对逻辑思维和数学计算知识的使用。但是大部分开发者没有去深度的针对算法领域去深入,而且有时候太深奥的算法也不常用,往往就忽略了。但是作为程序开发人员,无算法无编程,经典的算法还是要掌握的,本篇博文就来分享一下关于八皇后算法在前端领域的运用,记录一下,方便后期查阅使用。
什么是八皇后问题?
诞生:八皇后问题(Eight queens),是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。
八皇后问题表述:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转,和对角线对称变换的摆法看成一类,共有42类。
八皇后问题解题思路分析:
第一个皇后先放在第一行第一列;
第二个皇后放在第二行第一列,然后判断是否0K,如果不OK, 继续放在第二列、第三列,依次把所有列都放完,直到找到一个合适的为止;
第三个皇后,以此尝试放在第一列、第二列…,直到第八个皇后也能放在一个互不冲突的位置,最后就算是找到了一个正确解。
当得到一个正确解时,在栈回退到上一个栈的时候,就会开始回溯,也就是将第一个皇后,放到第一列的所有正确解,全部得到;
然后回过头继续第一个皇后放第二列,后面的操作继续循环执行1、2、3的步骤即可。
解释说明:理论上应该创建一个二维数组来表示棋盘,但是实际上可以通过算法用一个一维数组即可解决问题。
如array[8]={0,4,6,1,7,5,2,3}表示一个正解,对应array的下标表示第几行,即第几个皇后,array[i]=val , val表示第i+1个皇后,放在第i+1行的第val+1列。
注意:使用这种方式的效率可能比较低,可以使用其他算法对其进行优化,如贪心算法。
JS解决八皇后问题
通过JS来实现解决八皇后问题的方法,具体代码如下所示。
//方法一
function queen(array, current) {
if (current==array.length) {
console.log(array);
return;
}
for (var i = 0; i < array.length; i++) {
array[current] = i;
var flag = true;
for (var j = 0; j < current; j++) {
var ab = i - array[j];
if (array[j]==i||(ab>0?ab:-ab)==current-j) {
flag=false;
break
};
};
if (flag) {
queen(array,current+1);
}
};
};
queen([1,1,1,1,1,1,1,1],0);运行效果如下所示:
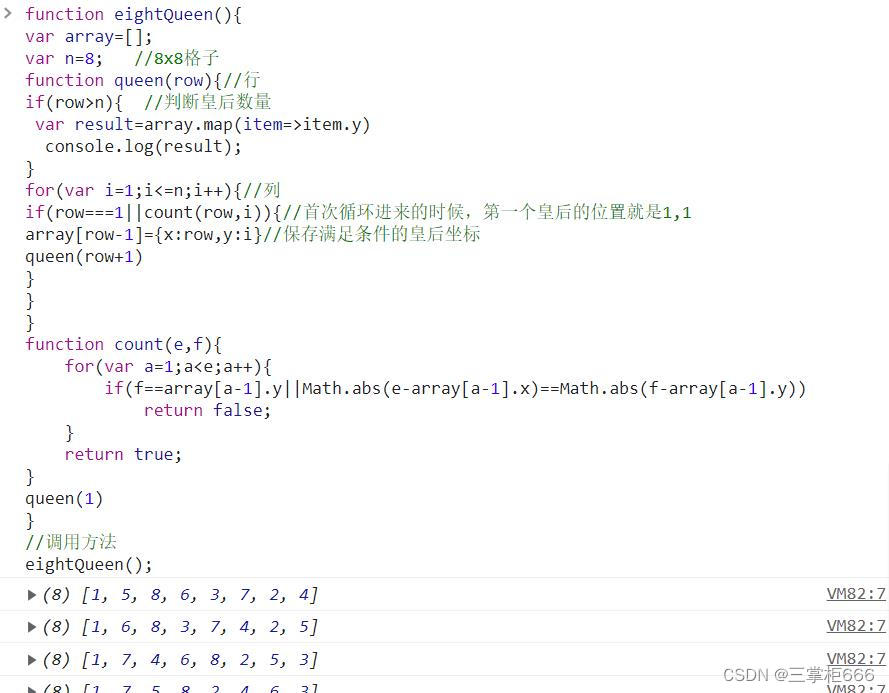
//方法二
function eightQueen(){
var array=[];
var n=8; //8x8格子
function queen(row){//行
if(row>n){ //判断皇后数量
var result=array.map(item=>item.y)
console.log(result);
}
for(var i=1;i
if(row===1||count(row,i)){//首次循环进来的时候,第一个皇后的位置就是1,1
array[row-1]={x:row,y:i}//保存满足条件的皇后坐标
queen(row+1)
}
}
}
function count(e,f){
for(var a=1;a
if(f==array[a-1].y||Math.abs(e-array[a-1].x)==Math.abs(f-array[a-1].y))
return false;
}
return true;
}
queen(1)
}
//调用方法
eightQueen();运行结果如下所示:
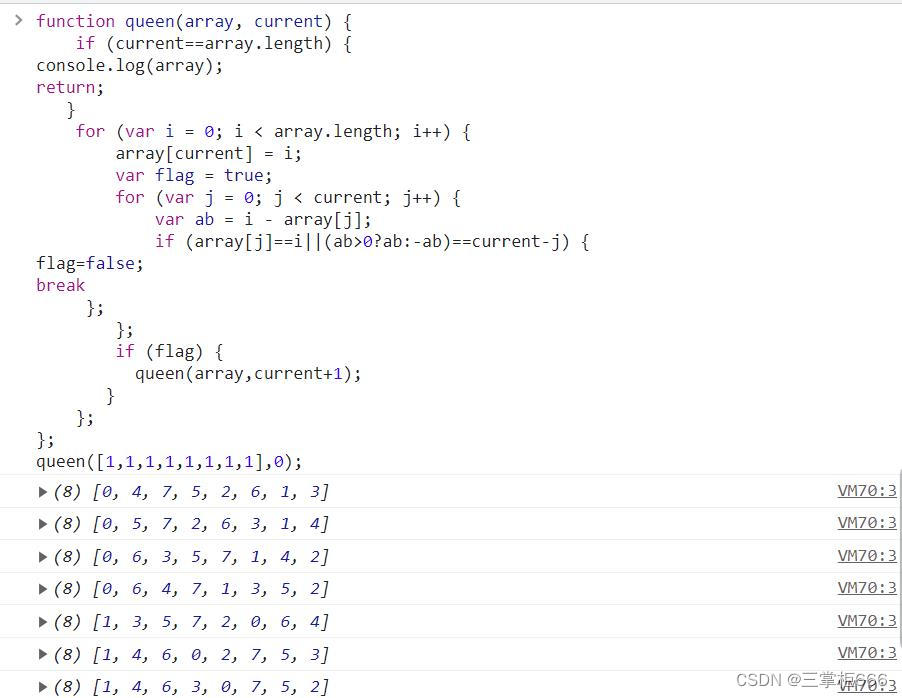
结论:需要枚举所有的搜索路径,当发现不满足求解条件的时候,就回溯到上一步,这也是为什么八皇后算法属于回溯算法的典型案例。
最后
通过本文关于前端开发中使用JS关于八皇后算法使用的介绍,虽然在大部分实际开发中使用到上述示例的可能性不大,但是还是要掌握对应的知识点,尤其是在求职面试过程中会涉及到前端相关的算法知识使用,所以还是要学会掌握的,尤其是从事前端开发不久的开发者来说尤为重要,是一篇值得阅读的文章,且在实际开发中也是必用知识点,所以说这个知识点是必备的,重要性就不在赘述。欢迎关注,一起交流,共同进步。