理论基础
动态规划是由前一个状态推导出来的, 而贪心是局部直接选取最优
五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
debug过程 : dp数组打印查看
509. 斐波那契数


参考

//动态规划的方法
//1.明确dp[i]含义:第i个数
//2.递推公式:dp[i] = dp[i - 1] + dp[i - 2]
//3.初始化: dp[0] = 0, dp[1] = 1
//4.遍历顺序: 从前往后
class Solution {
public:
int fib(int n) {
if (n < 2) return n;
vector<int>dp(n + 1, 0);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
//递归的方法
class Solution {
public:
int fn(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
return fn(n - 1) + fn(n - 2);
}
int fib(int n) {
return fn(n);
}
};
70. 爬楼梯


- dp[i] : 爬至第 i 阶楼梯总共的方法
- 递推公式 : dp[i] = dp[i-1] + dp[i-2],
- i 可以从 i-1 走一步上来,
- i 可以从 i-2 走两个上来,
- 所以 i 等于 [i-1] + [i-2]
- 初始化: n=0无意义, 所以从n=1开始初始化
- 遍历顺序: 从前向后遍历
class Solution {
public:
int climbStairs(int n) {
if (n <= 3) return n;
vector<int> dp(n + 1, 0);//索引: 0 1 ... n, 总共有n+1个元素
dp[1] = 1;
dp[2] = 2;
//dp[3] = 3;此处使用递归公式确定
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];//索引n代表第n阶楼梯
}
};
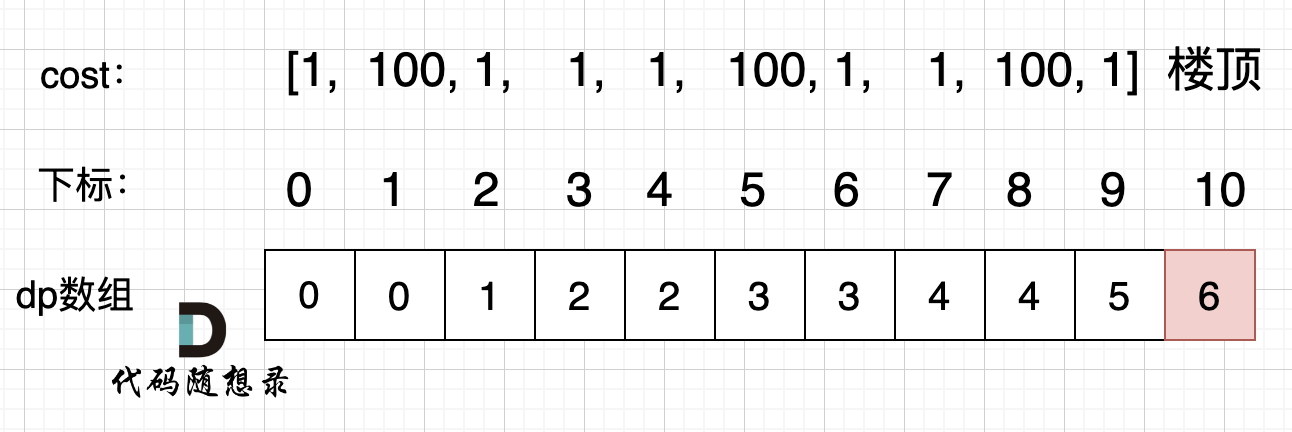
746. 使用最小花费爬楼梯


- dp[i] : 到达 i 的费用
- 递推公式: dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i-1]);
- 初始化 dp[0] = 0, dp[1] = 0 一开始不用耗费, 直接在 0 或 1 阶的楼梯上
- 遍历顺序: 从 0~n
在调试时确定其范围, 确定dp数组的大小

class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n+1, 0);
dp[0] = 0;
dp[1] = 0;
dp[2] = min(dp[0] + cost[0], dp[1] + cost[1]);
for (int i = 2; i <= n; i++) {
dp[i] = min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
}
return dp[n];
}
};