目录
齐次坐标
透视投影
透视投影的四棱锥体挤压为正交投影的长方体
变换规定
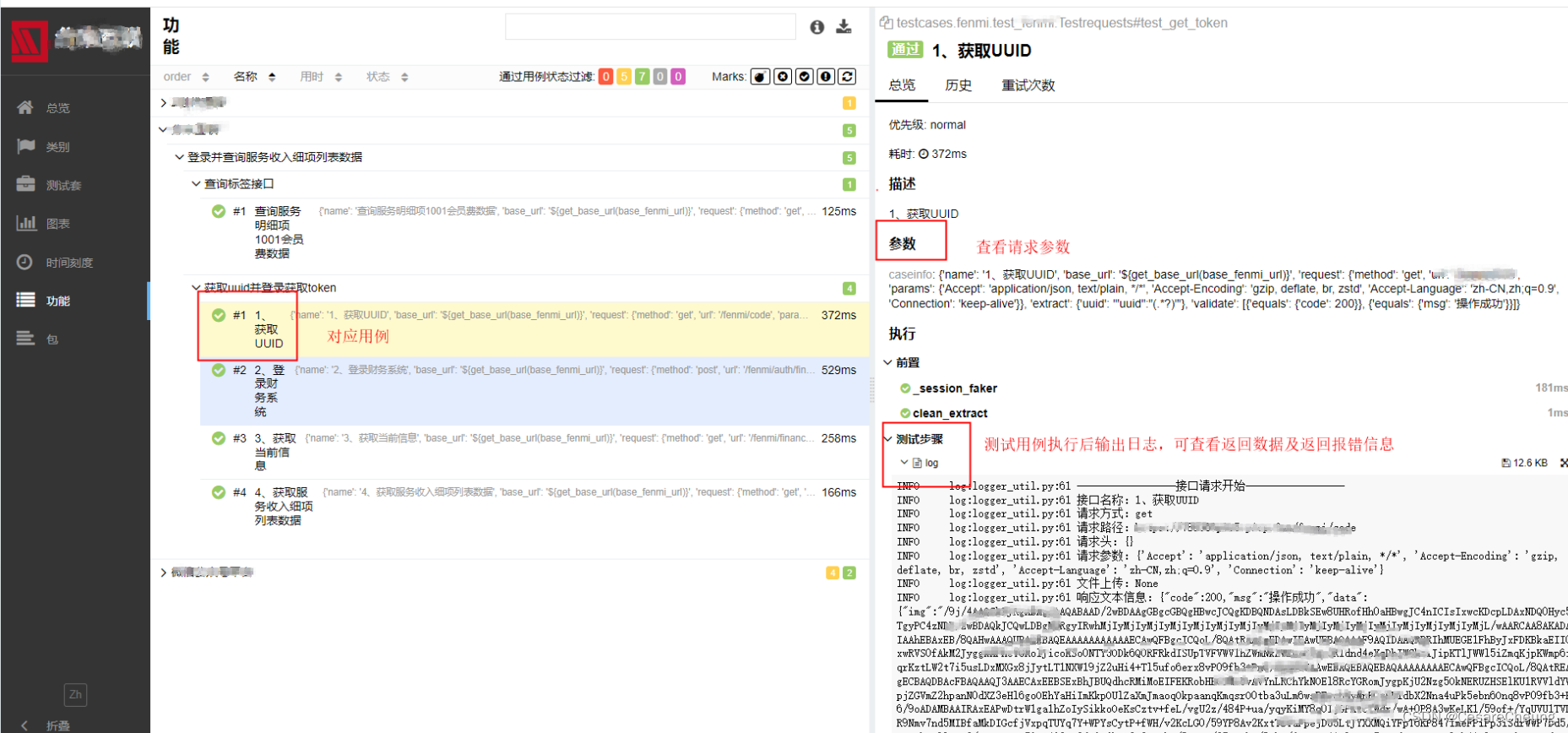
转换过程
观察1
观察2
关于任意一点挤压后向哪里移动的问题,简单推导了一下
齐次坐标
如下,(x, y, z, 1) 表示空间中的xyz点,让它每个分量乘以k,k!=0,得到的齐次坐标也是表示空间中的这个点,同样,乘以z,得到的也是xyz这个点

透视投影
从一个点往外延伸出来一个四棱锥,这个点就是相机,定义 远平面f 和 近平面n,透视投影视椎体的区别就在于它的远平面要比近平面更大,那么如何计算这个不规则的视体矩阵呢?
- 将透视相机的Frustum挤压为正交相机的Cuboid
- 再用正交投影矩阵相乘与上方变换矩阵相乘,即可得到最终的透视投影矩阵
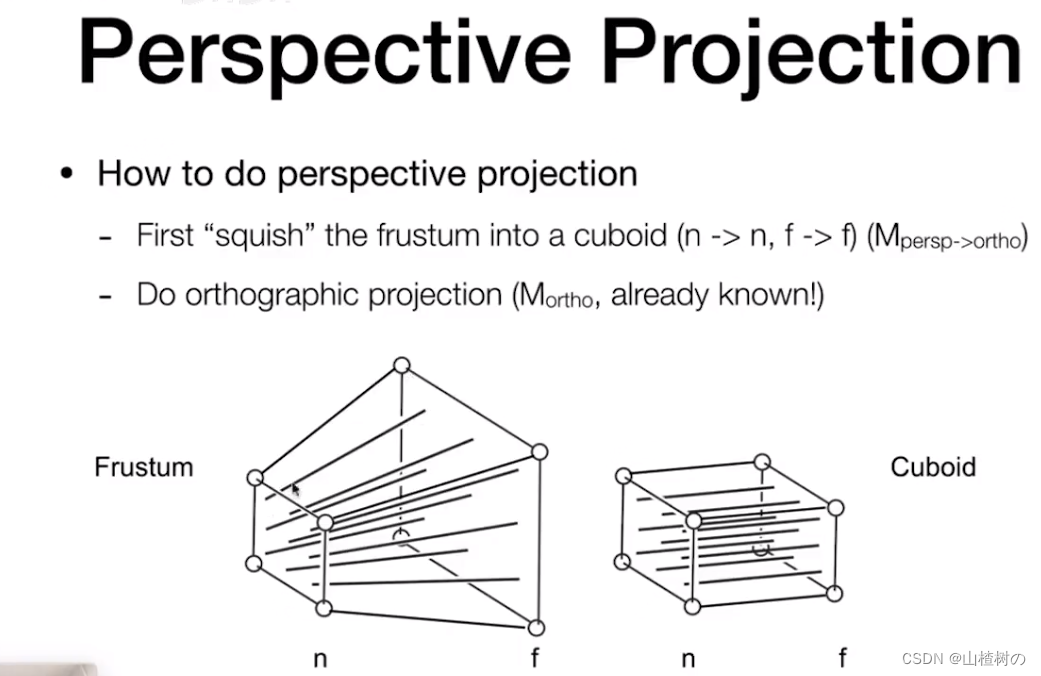
透视投影的四棱锥体挤压为正交投影的长方体
变换规定
- 近平面上的点,挤压后也不会变化
- 远平面上的点的z值是f,挤压后的z值仍然是f,它的z值不会发生变化,只是整体在向里面收缩
- 箭头指向的远平面中心点,挤压后仍然是中心点(0,0,f)
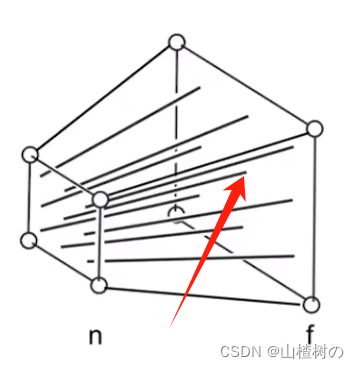
转换过程
如下,从侧面看向Frustum,蓝色箭头指向的是相机摆放的位置,上方向是Y,朝向-Z方向看,往右边看到的区域是近,远平面的一半
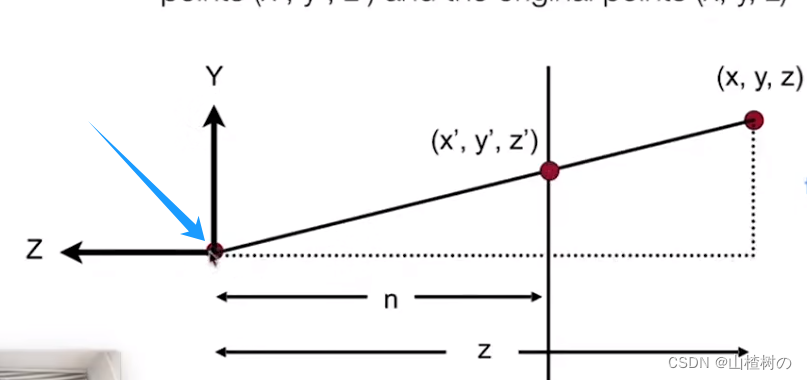
已知n,z,远平面上的xyz点,要把y挤压为 y',根据相似三角形可得 y'/y = n/z
满足如下规律

当然,对于x,同样满足相似三角形规律
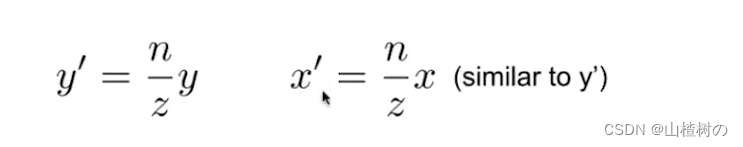
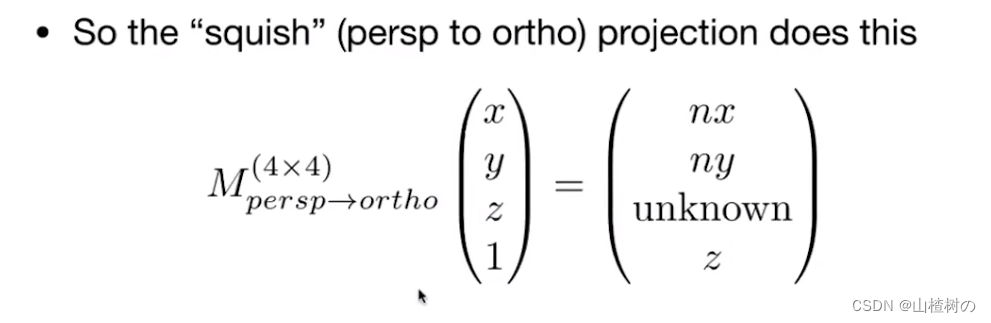
可得出结论,给定任何一点xyz,它被挤压后的点坐标一定是 (nx/z, ny/z, unkown, 1)T, 挤压的变换的矩阵左乘xyz点即可得到这个点
根据齐次坐标性质,另如下中间的齐次坐标点同乘z,得到的坐标依然不变,那么经过挤压变换后的点,依然可以用右边齐次坐标表示

现在,已知挤压变换后的 x y w 三个分量, 已经可以写出变换矩阵的 1 2 4 行的值
那么,第三行的行向量又是多少呢?
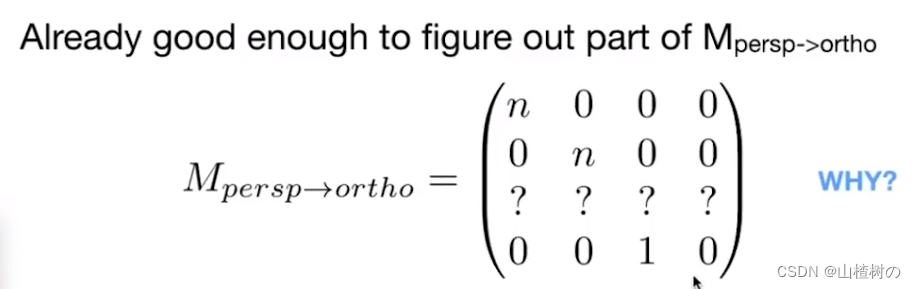
观察
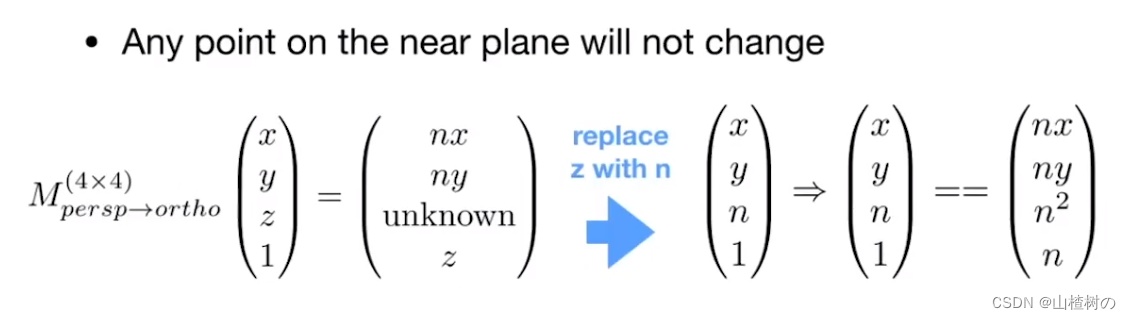
- 任何一个点在近的平面上经过挤压后不会发生任何变化,也就是,对于近平面上的点(x, y, n, 1) 经过矩阵变换后得到的点仍然是 (x, y, n, 1) (近平面的z值为n)
- 任何一个点在远的平面上经过挤压后它的xy值会朝里挤,但z值不会发生变化
观察1
挤压后的近平面上的点依然是(x, y, n, 1),另每个分量乘以 n,得到(nx,ny,n^2, n),依然表示这个点,那么我们就探讨什么样的挤压矩阵左乘(x, y, n, 1) 会 得到 (nx,ny,n^2, n)
上面已经推导出挤压变换矩阵的第 1 2 4 行向量,思考: 第三行的向量 *(x, y, n, 1)= n^2
由于点乘的结果是n^2,则必定跟xy没关系,讨论 A和B的取值即可
这里A和B的值并不能确定,因为 A=n, B=0 成立, A=0, B=n^2 也成立

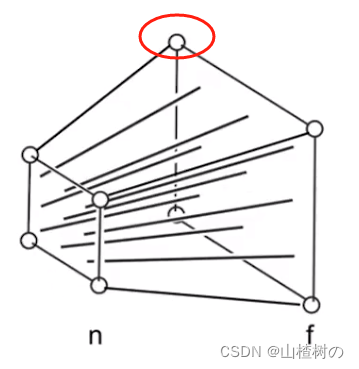
观察2
远平面的中心点经过挤压后它的坐标仍不会变化,依然是(0,0,f)由于w分量需要存储z值,另分量同乘以f,得到下图最右侧齐次坐标,从上 近平面,我们依然讨论挤压矩阵的第三行向量, 向量 * (0, 0, f, 1) = f^2

综观察1,观察2,可以得出如下两个等式

n, y已知,两个式子,两个未知数, 很容易得出 A,B的值
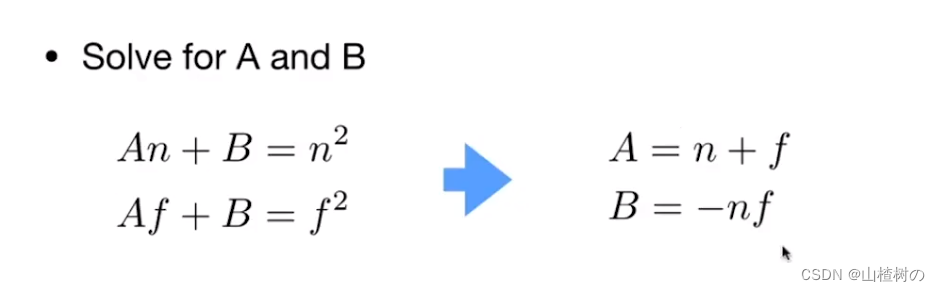
至此可解出 Mpersp -> ortho 透视投影的Frustum挤压为正交相机的Cuboid 的变换矩阵
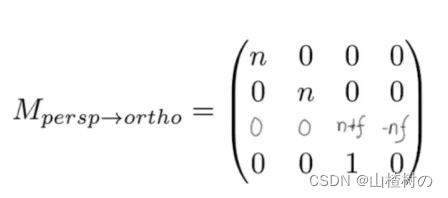
接下来,将 挤压变换矩阵 乘以 正交投影的投影矩阵 即可求出最终的透视投影矩阵
正交投影矩阵推导:Games101 正交投影矩阵推导-CSDN博客

关于任意一点挤压后向哪里移动的问题,简单推导了一下