20 世纪 50 年代,数学家恩斯特·施特劳斯(Ernst Straus)提出了一个有趣的问题:在一个侧壁由理想反射镜构成的任意形状的空房间里,一个点光源是否总能照亮整个房间?诺贝尔奖获得者罗杰·彭罗斯(Roger Penrose)爵士巧妙地回答了这个问题,他设计了一个包含不能被照亮区域的房间,因此被称为“无法被完全照亮的彭罗斯房间”(以下简称“彭罗斯房间”)。然而,彭罗斯房间真的不能被完全照亮吗?在今天这篇文章中,我们将使用 COMSOL Multiphysics 软件进行模拟,看看情况是不是像他所回答的那样,并讨论了射线光学的基本假设。
照明问题
当你次听到这个问题时,可能不能立即明白它到底在问什么。我们以下图中的示例来说明。如左图所示,一个二维房间的镜面墙可以是任意形状,光源可以位于房间内的任何位置。在这种特殊情况下,很容易想象整个房间都会被光源照亮,这一点也在右图中的射线追踪模拟中得到了证实。本质上,施特劳斯的问题是:是否存在这样一种房间形状设计,当在其中放置点光源时,某些区域不会被照亮。
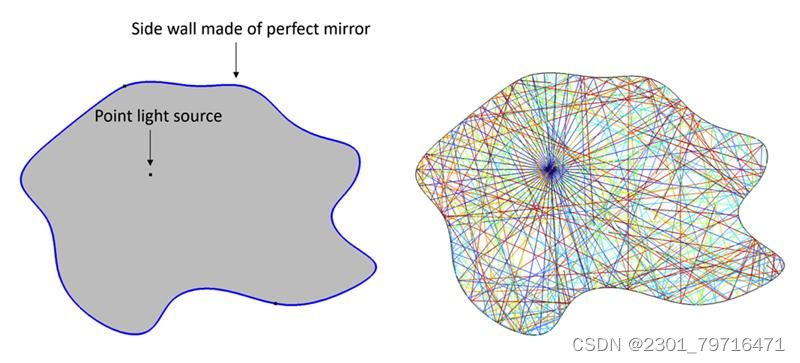
图片一个任意形状的空房间,周围是完美的镜子,房间内放有一个点光源(左)。射线追踪模拟显示整个房间都被点光源照亮(右)。
看到这个问题,我立刻想到,也许一个拐角很尖的房间可以阻止某些区域被照亮。但是,你可能已经猜到了:如果可以这么容易地计算出一个不能被照亮的房间的形状,那么对于科学界来说,这就不是一个有趣的问题了。我们可以看到,只要有足够的时间,灯光总会照亮整个房间。在这一点上,你可能不相信并认为你可以设计一个不能被照亮的房间。如果你准备接受这个挑战,欢迎你随时使用 COMSOL 射线光学模块来试一试。

带有尖角的房间完全被点光源照亮。
无法被完全照亮的彭罗斯房间
这个棘手的问题终被杰出的 2020 年诺贝尔物理学奖得主罗杰·彭罗斯解决了。如下图所示,他的设计初看并不显眼。这个房间由顶部和底部的两个椭圆形墙壁和一个带有两个“伞”形切口的矩形区域组成。设计的要求是,将顶壁和底壁描述为椭圆 图片,并且椭圆的焦点与伞的角点重合。一些细节,诸如 图片 和 图片 的具体值、伞的形状、伞的宽度等都不会改变房间的属性。
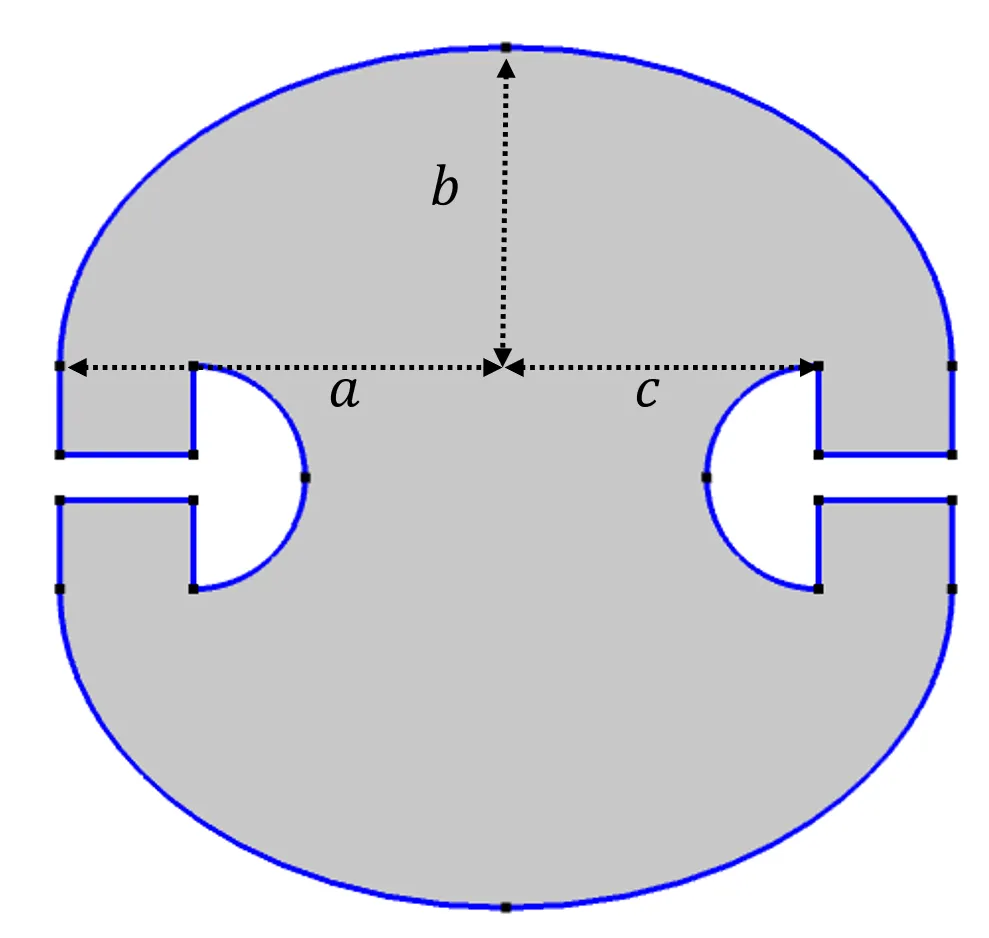
无法被完全照亮的彭罗斯房间的设计。
让我们使用射线光学模块来看看它是否有效!在下面的动画中,我们将点光源放置在一些具有代表性的位置——中心、上半部分和左边伞的左侧(如果我们假设伞是直立的,那么光源就位于伞的下方),光线从这些点各向同性地发射。显然,在任何情况下,都存在未被光照亮的区域。当光源被放置在伞的下方时,光线甚至不会传播到房间的下半部分。请注意,这并不是因为时域仿真运行时间不够长。即使时间接近无限长,这些阴影区域仍然没有被照亮。
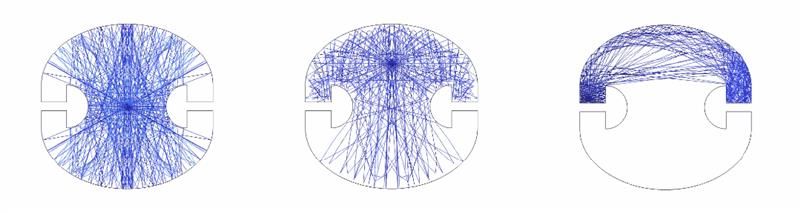
将点光源放置在彭罗斯房间的不同位置进行射线追踪模拟。在任何情况下,总是存在未照亮的区域。
彭罗斯房间的独特性来自于椭圆镜的特殊性。你可能还记得,在大学光学课上学过,从椭圆镜的一个焦点发出的光将聚焦在另一个焦点上,下面左下方的动画演示了这一特性。椭圆镜另一个鲜为人知的特性是,当光线从椭圆的一个焦点和其近的顶点之间发出时,它只会到达另一个焦点和另一个顶点之间的一点,永远不会与焦点之间的长轴相交,这个特性在下面中间的动画中进行了演示。此外,从两个焦点之间发出的光永远不会与每个焦点和其近的顶点之间的长轴相交,如下面右边的动画所示。

左:在焦点处发射的光线只会在焦点处与长轴相交。中:在焦点和近的顶点之间发射的光线不会与焦点之间的长轴相交。右:在两个焦点之间发射的光线只会与焦点之间的长轴相交。
考虑到这些特性,我们可以将彭罗斯房间划分为如下所示的区域。再次提醒,在彭罗斯的设计中,椭圆的焦点与伞的边缘重合。因此,我们知道:
放置在A1里面的一个点光源,只会照亮 ,A1,B1和 A2,因为它永远不能与焦点之间的椭圆长轴相交并进入 C1 区域。
放置在 B1 的一个点光源,不能照亮 A3 和 A4,因为光线只能进入下椭圆的两个焦点之间的下半部。因此,它们永远不能与焦点和顶点之间的长轴相交并进入 A3 和 A4。
同样的原因,放置在C1 的一个点光源,不能照亮 A1, A2, A3和 A4。
由于对称性,放置在房间下半部分相应区域的光源也会产生相同的效果。因此,我们可以得出结论,无论点光源放置在房间内的哪个位置,彭罗斯房间都会存在不能被照亮的区域。
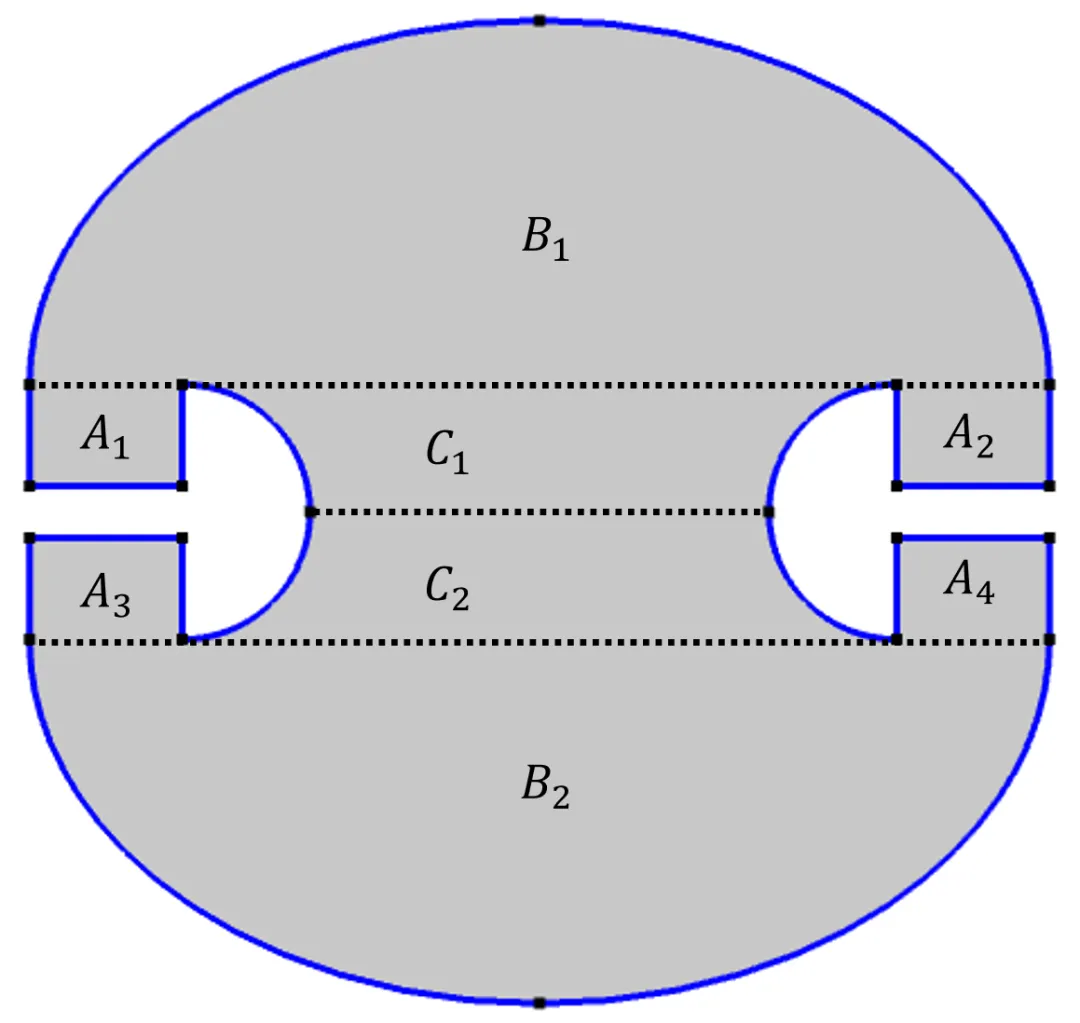
将房间划分为不同的区域。放置在 A1 区域的一个光源只会照亮 A1, B1和 A2区域;放置在 区域的 一个光源不会照亮A3 和 A4。放置在 C1 的一个光源不会照亮 A1,A2,A3 和 A4。
让光存在:照亮没有照亮的区域
上文中的射线追踪模拟似乎显示了令人信服的结果,证实了房间无法被照亮,但真的是这样吗?我们不能忘记射线光学的基本假设:光的波长远远小于与光相互作用的物体的大小,因此,衍射效应可以完全忽略。我们记得 图片 是描述房间顶部和底部墙壁的椭圆的长轴。射线光学模拟本质上是假设波长 <<。如果我们有一个大小在米级尺度的真实房间,光源在可见光谱范围内(约 500nm 波长),这个假设是成立的。但是,如果我们缩小房间或者增加光的波长,使 图片 与 图片 大小相当,那会怎样?
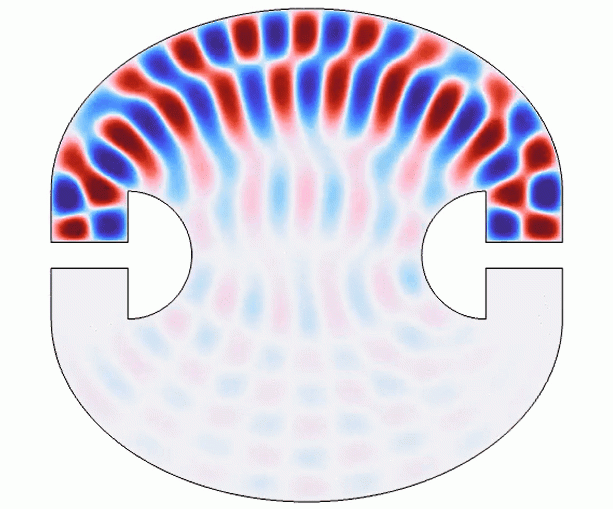
为了测试这一点,我们现在使用波动光学模块进行全波模拟。一个点[线电流(面外)]放置在左上角的伞的下方(图片 区域),类似于上面显示的房间的第三个射线追踪动画。线电流用作点源,发射出电场指向面外方向的圆柱形波。在频域中模拟波长增加时的场分布,如下图所示。正如预期的那样,在 图片(左上)时,场分布与射线追踪模拟相似。场似乎没有穿过房间的下半部分。然而,随着波长变长,衍射更加突出,场渗入到房间的下半部分。在 图片(左下)和 图片(右下)时,很明显之前没有被照亮的区域被照亮了!

图片在 图片, 图片, 图片 和 图片 时,模拟的频域中的场分布。在较短的波长下,场分布与射线追踪结果类似。然而,在较长的波长下,场会穿透到之前由于衍射而没有被照亮的区域。图中绘制了电场的模。
除了使用电磁波,频域接口来展现达到稳态时的场分布外,使用电磁波,瞬态接口运行时域仿真可以通过视图查看波的传播和衍射过程。
由位于房间上半部的左侧伞的“下方”(左侧)的线电流发出的面外电场,并在时域中进行了模拟。由于衍射,电场渗入到房间的下半部分。波长为 。
波干涉
到目前为止,我们的模拟似乎表明彭罗斯房间只有在忽略衍射效应的前提下才能不被照亮。但是,我们必须意识到,不能急于得出这个结论,实际情况更加复杂。当光的波动性出现时,需要考虑另一个重要现象——干涉。通过查看频域仿真结果,我们可以看到,在许多区域,电场模实际上为零。这是因为出射波和衍射波相互干涉,形成一个场强存在零点的驻波模式。因此,从某种意义上说,这些区域在达到稳态时并未被照亮。如果等待足够长的时间,总会有没有光线的区域。从时域角度来看,当光波次传播到这些区域时,它们在一段时间内被照亮,直到衍射波到达后抵消电场。从这个意义上说,整个房间至少在一段时间内都被照亮了。总之,整个房间有没有被照亮取决于你的解释。重要的是,我们可以看到,在不同的尺度上,光学现象看起来可能大不相同。作为仿真工作者,我们始终需要牢记波动光学和射线光学之间的根本区别,以及与之相关的独特现象。
结语
除了这个有意思的数学谜题之外,彭罗斯房间是展示波动光学和射线光学之间根本区别的一个很好的例子。在不同的假设下,同一个问题的结论可能完全不同。它还回答了很多初学者提出的问题:COMSOL? 软件有两个光学模块。我应该使用波动光学模块还是射线光学模块来模拟我的光学问题?简单的回答是:我们研究的几何尺寸远大于相关波长,如可见光与相机透镜系统的交互或街道上运行的激光雷达,那么使用射线光学模块就非常合适。另一方面,如果我们关注的是尺寸与波长相当或更小的纳米粒子的光散射现象,那么使用波动光学模块或 RF 模块进行全波模拟是不可避免的。同时,模块的选择还取决于你感兴趣的物理量和过程。例如,射线光学模拟可以生成光传播路径,而波动光学模拟可以渲染完整的电场分布。
为你的仿真选择合适的模块不仅可以确保仿真结果的准确性,还可以节省大量的仿真时间。