【Python机器学习】聚类算法的对比与评估—

数据探查：

我们将k均值、DBSCAN和凝聚聚类算法应用于Wild数据集中的Labeled Faces，并查看它们是否找到了有趣的结构。我们将使用数据的特征脸表示，它由包含100个成分的PCA(whiten=True)生成：


people=fetch_lfw_people(data_home = "C:\\Users\\86185\\Downloads\\",min_faces_per_person=20,resize=.7)
image_shape=people.images[0].shape
mask=np.zeros(people.target.shape,dtype=np.bool_)
for target in np.unique(people.target):
    mask[np.where(people.target==target)[0][:50]]=1

X_people=people.data[mask]
y_people=people.target[mask]

pca=PCA(n_components=100,whiten=True,random_state=0)
pca.fit_transform(X_people)
X_pca=pca.transform(X_people)

与原始像素相比，这是对人脸图像的一种语义更强的表示，它的计算速度更快。

用DBSCAN分析人脸数据：

dbscan=DBSCAN()
labels=dbscan.fit_predict(X_pca)
print('标签：{}'.format(np.unique(labels)))

可以看到，所有返回的标签的-1，因此所有数据都被DBSCAN标记为噪声。我们可以改变两个参数来改进这一点：

1、增大eps，从而扩展每个点的邻域；

2、缩小min_samples，从而将更小的点视为簇。

首先尝试改变min_samples：

dbscan=DBSCAN(min_samples=3)
labels=dbscan.fit_predict(X_pca)
print('标签：{}'.format(np.unique(labels)))

可以看到，由3个点构成的组，所有点也被标记为噪声，因此需要增大eps：

dbscan=DBSCAN(min_samples=3,eps=15)
labels=dbscan.fit_predict(X_pca)
print('标签：{}'.format(np.unique(labels)))

使用更大的eps（15），只得到了单一簇和噪声点。我们可以利用这一结果找出噪声相对于其他数据的形状。

print('噪声、簇内点：{}'.format(np.bincount(labels+1)))

可以看到，噪声只有37个，因此可以查看所有的噪声点：


noise=X_people[labels==-1]
fig,axes=plt.subplots(5,9,subplot_kw={'xticks':(),'yticks':()},figsize=(12,4))
for image,ax in zip(noise,axes.ravel()):
    ax.imshow(image.reshape(image_shape),vmin=0,vmax=1)
plt.show()

可以看到，有些人脸图像在喝水（拿杯子）或者戴帽子等，猜测这就是被标记为噪声的原因。

这种类型的分析（尝试找出“奇怪的那一个”）被称为异常值检测。如果这是一个真实的应用，那么我们可以去尝试更好的裁切图像，以得到更均匀的数据。

如果想找到更有趣的簇，而不是一个非常大的簇，可以把eps设置的更小。

来看一下不同eps取值的结果：


for eps in [1,3,5,7,9,11,13]:
    print('\neps:{}'.format(eps))
    dbscan=DBSCAN(eps=eps,min_samples=3)
    labels=dbscan.fit_predict(X_pca)
    print('簇类别：{}'.format(np.unique(labels)))
    print('簇的大小：{}'.format(np.bincount(labels+1)))

对于较小的eps，所有的点都被标记为噪声。

eps=7时，会得到很多噪声点和一些较小的簇；

eps=9时，仍然会得到很多噪声点，但是会得到一个比较大的簇和一个较小的簇；

从eps=11开始，就只能得到一个较大的簇和一些噪声。

较大的簇从来没有超过过一个，最多有一个较大的簇包含大多数点，还有一些较小的簇。

我们可以通过研究eps=7时，将7个较小的簇中的点全部可视化来深入研究这个聚类：


dbscan=DBSCAN(min_samples=3,eps=7)
labels=dbscan.fit_predict(X_pca)
for cluster in range(max(labels)+1):
    mask=labels==cluster
    n_images=np.sum(mask)
    fig,axes=plt.subplots(1,n_images,figsize=(n_images*1.5,4),subplot_kw={'xticks':(),'yticks':()})
    for image,label,ax in zip(X_people[mask],y_people[mask],axes):
        ax.imshow(image.reshape(image_shape),vmin=0,vmax=1)
        ax.set_title(people.target_names[label].split()[-1])
    plt.show()

有一些簇对应这个数据集中一些脸部非常不同的人。

每个簇的人脸方向和面部表情也是固定、相似的。而有些簇中虽然包含多个人的面孔，但他们的方向和表情都比较相似。

用k均值分析人脸数据：

我们可以看到，利用DBSCAN无法创建多余一个较大的簇。凝聚聚类和k均值更可能创建均匀大小的簇。但我们需要设置簇的目标个数。

我们可以将簇设置为数据集中的已知个数，虽然无监督聚类算法不太可能完全得到他们。相反，我们可以先设置一个比较小的簇个数，这样我们可以分析每个簇：


km=KMeans(n_clusters=10,random_state=0)
label_km=km.fit_predict(X_pca)

print('簇的大小（k均值）：{}'.format(np.bincount(label_km)))

可以看到，k均值聚类将数据划分为大小相似的簇，大小在60到363之间，这与DBSCAN非常不同。

通过将簇中心可视化来进一步分析k均值的结果。

由于我们是在PCA生成的表示中进行聚类，因此我们需要使用pca.inverse_transform将簇中心旋转回到原始空间并可视化：


fig,axes=plt.subplots(2,5,subplot_kw={'xticks':(),'yticks':()},figsize=(12,4))
for center,ax in zip(km.cluster_centers_,axes.ravel()):
    ax.imshow(pca.inverse_transform(center).reshape(image_shape),vmin=0,vmax=1)
plt.show()

k均值找到的簇中心是非常平滑的人脸。因为每个簇中心都是60到363张人脸图像的平均。使用降维的PCA表示，可以增加图像的平滑度。聚类似乎捕捉到人脸的不同方向、不同表情、以及是否有衬衫扣子之类的特征。

我们对每个簇中心给出了簇中5张最经典的图像（也就是该簇中与簇中心距离最近的图像）与5张最不典型的图像（也就是该簇中与簇中心距离最远的图像）：

mglearn.plots.plot_kmeans_faces(km,pca,X_pca,X_people,y_people,people.target_names)
plt.show()

可以看到，“非典型的”点与簇中心不太相似，似乎分配有些随意。这可以归因于一下原因：k均值对所有数据点进行划分，不想DBSCAN那样具有噪声点的概念。

利用更多数量的簇，算法可以找到更细微的区别，但添加更多的簇会使得人工检查更为困难。

用凝聚聚类分析人脸数据：

下面看一下凝聚聚类的结果：

agglomerative=AgglomerativeClustering(n_clusters=10)
label_agg=agglomerative.fit_predict(X_pca)

print('簇的大小（凝聚聚类）：{}'.format(np.bincount(label_agg)))

凝聚聚类生成的也是大小相近的簇，大小在49到553之间，这比k均值生成的簇更不均匀，但比DBSCAN生成的簇更加均匀。

我们可以通过计算ARI来度量凝聚聚类和k均值给出的两种数据划分是否相似：

km=KMeans(n_clusters=10,random_state=0)
label_km=km.fit_predict(X_pca)

print('ARI:{:.2f}'.format(adjusted_rand_score(label_agg,label_km)))

ARI只有0.09，说明labels_agg和labels_km这两种聚类的共同点很少，原因在于：对于k均值，原理簇中心的点似乎没有什么共同点。

下面绘制树状图，但是限制了数的深度，要不然全部呈现2063个数据点，图像无法阅读：

linkage_array=ward(X_pca)
plt.figure(figsize=(20,5))
dendrogram(linkage_array,p=7,truncate_mode='level',no_labels=True)
plt.xlabel('数据点')
plt.ylabel('簇 间距')
plt.show()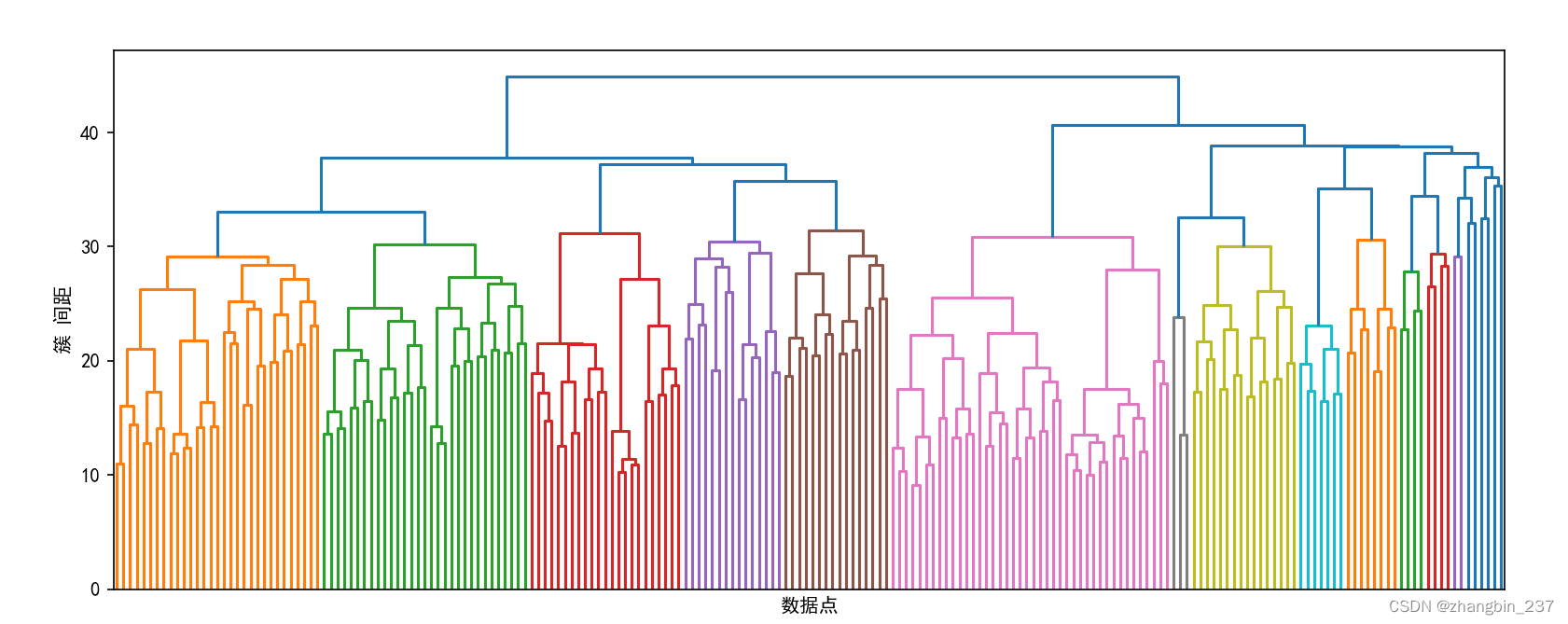

想要创建10个簇，我们要在顶部有10条竖线的位置将树横切。

我们将10个簇可视化。

在凝聚聚类内，没有簇中心的概念（虽然我们计算了平均值），我们芝士给出了每个簇的前几个点。


n_cluster=10
for cluster in range(n_cluster):
    mask=label_agg==cluster
    fig,axes=plt.subplots(1,10,figsize=(15,8),subplot_kw={'xticks':(),'yticks':()})
    axes[0].set_ylabel(np.sum(mask))
    for image,label,asdf,ax in zip(X_people[mask],y_people[mask],label_agg[mask],axes):
        ax.imshow(image.reshape(image_shape),vmin=0,vmax=1)
        ax.set_title(people.target_names[label].split()[-1],fontdict={'fontsize':9})
    plt.show()

虽然某些簇似乎具有语义上的主题，但其实很多簇都太大而实际上很难是均匀的。

为了得到更均匀的簇，我们可以再次运行算法，把簇设置为40个，并挑选一些特别的簇。

n_cluster=40
for cluster in [10,13,19,22,36]:
    mask=label_agg==cluster
    fig,axes=plt.subplots(1,15,figsize=(15,8),subplot_kw={'xticks':(),'yticks':()})
    cluster_size=np.sum(mask)
    axes[0].set_ylabel('#{}:{}'.format(cluster,cluster_size))
    for image,label,asdf,ax in zip(X_people[mask],y_people[mask],label_agg[mask],axes):
        ax.imshow(image.reshape(image_shape),vmin=0,vmax=1)
        ax.set_title(people.target_names[label].split()[-1],fontdict={'fontsize':9})
    for i in range(cluster_size,15):
        axes[i].set_visible(False)
    plt.show()