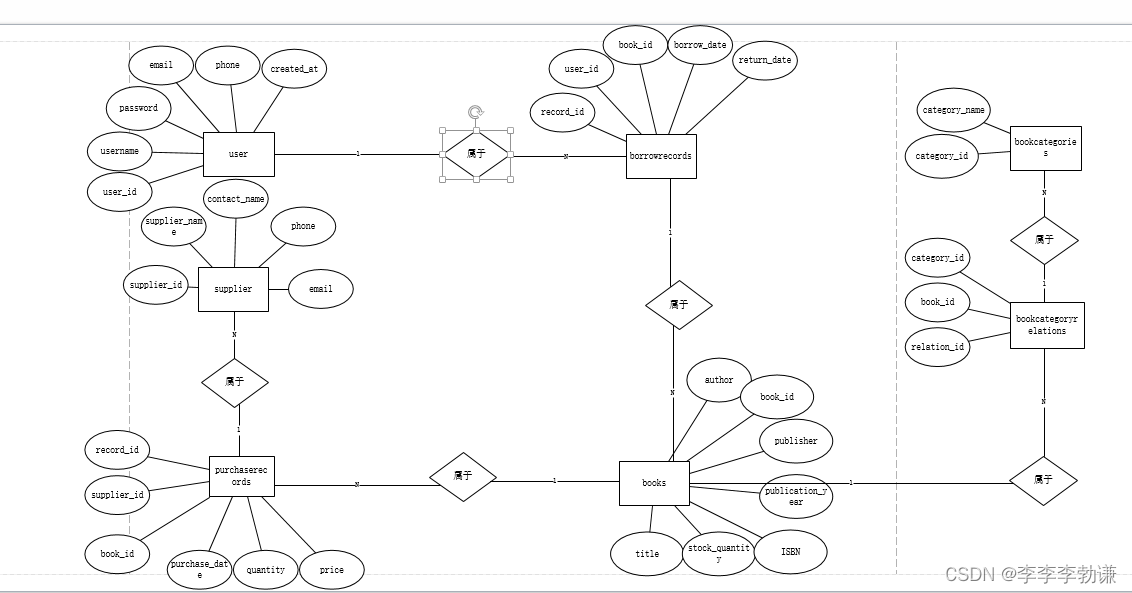
三相PMSM的数学模型是一个比较复杂且强耦合的多变量系统。为了便于后期控制器设计，必须选择合适的坐标变换对数学模型进行降阶和解耦变换。

1、什么是Clark变换

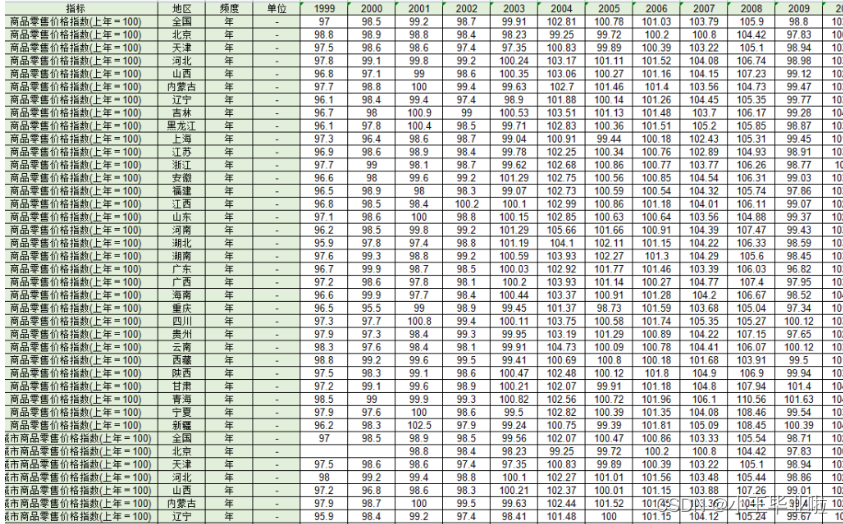
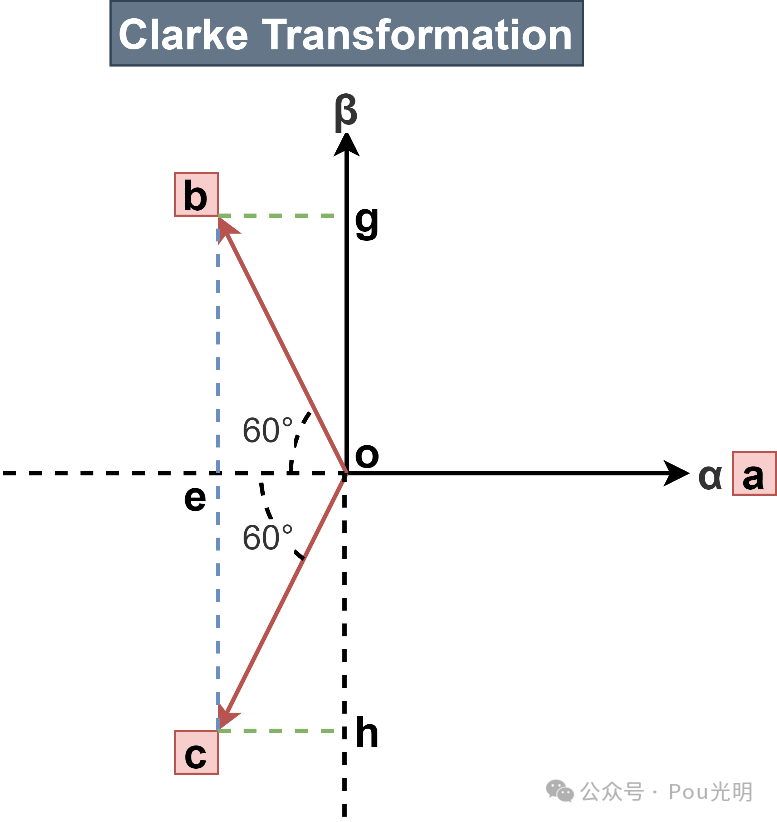
静止abc轴系与αβ轴系如上图。为满足功率不变约束，在图中设αβ轴系中定子绕组以及转子绕组的的有效匝数均为abc轴系每项绕组的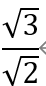倍。

磁动势等效是坐标变换的基础和原则。因为只有这样，坐标变换后才不会改变电机内的气隙磁场分布，才不会影响机电能量转换和电磁转矩生成。

              变换过程的推导，从计算上来讲是将是二维下的三个向量变为两个向量，算出一组两个线性无关的向量。直接利用投影即可。

计算过程：

已知三相坐标系的相位依次相差120°且αβ为正交坐标系。将α轴与a轴重叠，将向量a沿着原点O的方向延长做一条辅助线，∠boe和∠coe等于60°。    

计算向量b和向量c到α轴的投影长度：

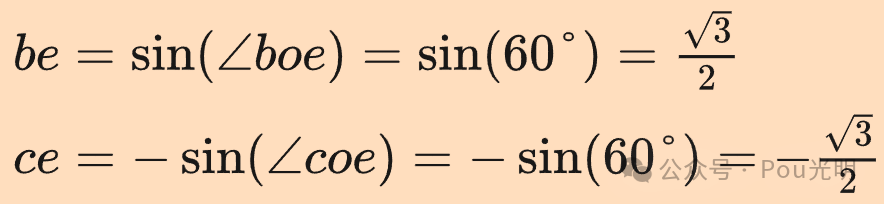
因为向量c在α轴的下方所以投影为负。

同理可计算向量b和向量c到β轴的投影长度。

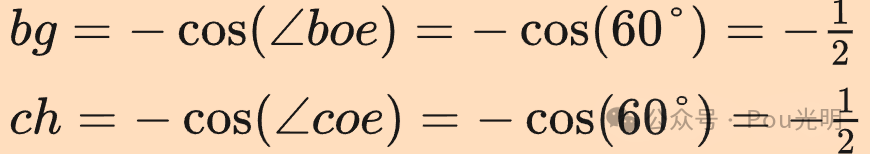
组合基变换矩阵：

2、等幅值变换

基尔霍夫电流定律：

所有进入某个节点的电流的总和等于所有离开这个节点的电流的总和。假设进入某节点的电流为正值，离开这个节点的电流为负值，则所有设计这个节点的电流的代数和等于零。    

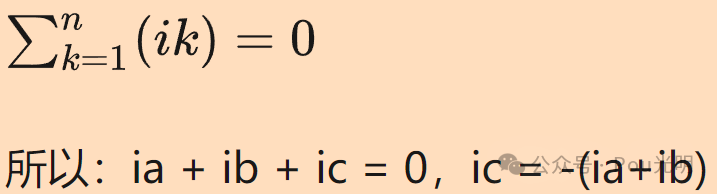
使用ia和ib将公式中的ic消除后的公式：

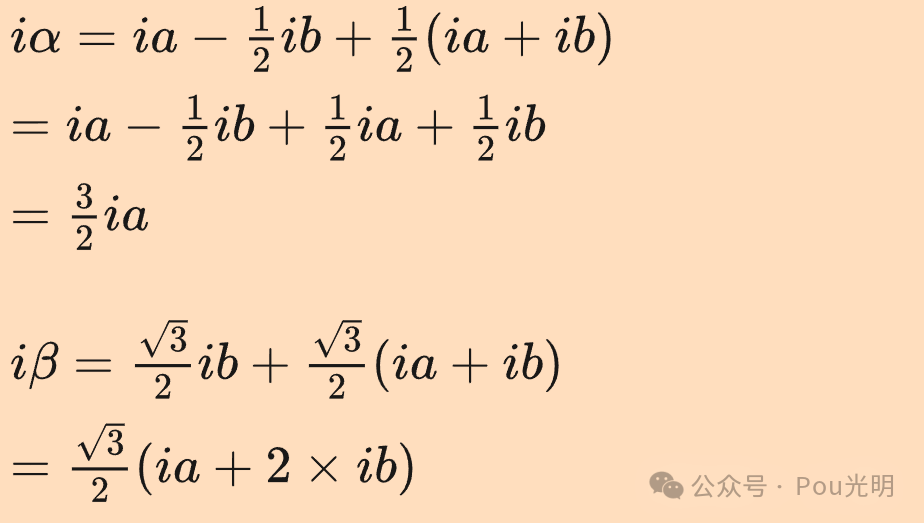
等幅值变换：

如果采用功率不变作为约束，系数为。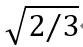

变换矩阵可记作：。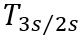

        欢迎关注：