优选算法2

news2024/10/9 20:25:29

五、位运算

常见位运算总结

&：有0就是0；

|：有1就是1

^：相同为0，相异就是1/无进位相加

给定一个数n,确定它的二进制表示中的第x位是0还是1：二进制中权值最小的是第0位，所以int整型是从第0位到第31位。于是n>>x &1就可以了

将一个数n的二进制表示的第x位修改成为1： (1<<x) | n

将一个数n的二进制表示的第x位修改成为0：(~(1<<x)) & n 

提取一个数n的二进制表示中最右侧的1：n&(-n)，正数变成负数的二进制表示就是按位取法再加1。-n的本质是将最右侧的1的左边区域（不包括最右侧的1也就是当前位置）全部变成相反，其余的都不变。

干掉一个数n二进制表示中最右侧的1，也就是将这个1变成0：n&(n-1) ,n-1的本质是将最右侧的1右边的区域（包含1）全部变成相反。

异或：a^a=0；a^0=a；a^b^c=a^(b^c)；交换律；采用无进位相加很容易证明 

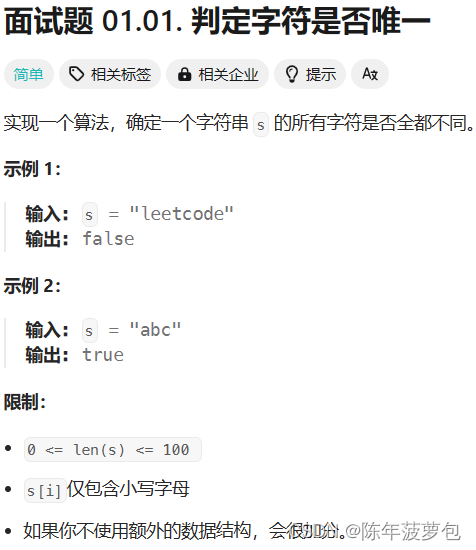
 1.判断字符是否唯一


采用位图的思想：因为单独的一个整型变量就有32位比特位

优化点：鸽巢原理，也就是如果字符串的长度超过26，必定存在重复字符。

class Solution {
public:
    bool isUnique(string astr) 
    {
        //利用鸽巢原理进行优化
        if(astr.size()>26) return false;
        int bitmap=0;
        for(auto ch:astr)
        {
            //判断字符出现在哈希表中
            if((1<<(ch-'a')) & bitmap) return false;
            //将当前字符加入到位图中
            else bitmap+=(1<<(ch-'a'));//bitmap |= (1<<(ch-'a'))
        }
        return true;
    }
};

2.丢失的数字

class Solution {
public:
    int missingNumber(vector<int>& nums) 
    {
        int n=nums.size()+1;
        int result=0;
        for(auto ch:nums) result^=ch;
        for(int i=0;i<n;i++) result^=i;
        return result;
    }
};

3.两整数之和（巧妙）



利用异或的无进位相加，然后找到需要进位的地方。通过a&b可以找到需要进位的地方，因为只有1&1才能得到1，而这也是我们需要进位的地方。（a&b)<<1才是我们需要进位的位置。

class Solution {
public:
    int getSum(int a, int b) 
    {
        while(b)
        {
            int temp_a=a;
            a=temp_a^b;//先算出无进位相加的结果
            b=(temp_a&b)<<1;//算出进位
        }
        return a;
    }
};

4.只出现一次的数字


 

class Solution {
public:
    int singleNumber(vector<int>& nums) 
    {
        int ret=0;
        for(int i=0;i<32;i++)//依次去修改ret中的每一位
        {
            int sum=0;//统计nums中第i比特位出现1的次数
            for(auto ch:nums)
                if(ch & (1<<i)) sum++;
            if(sum%3) ret |= (1<<i);//修改ret的第i比特位
        }
        return ret;
    }
};

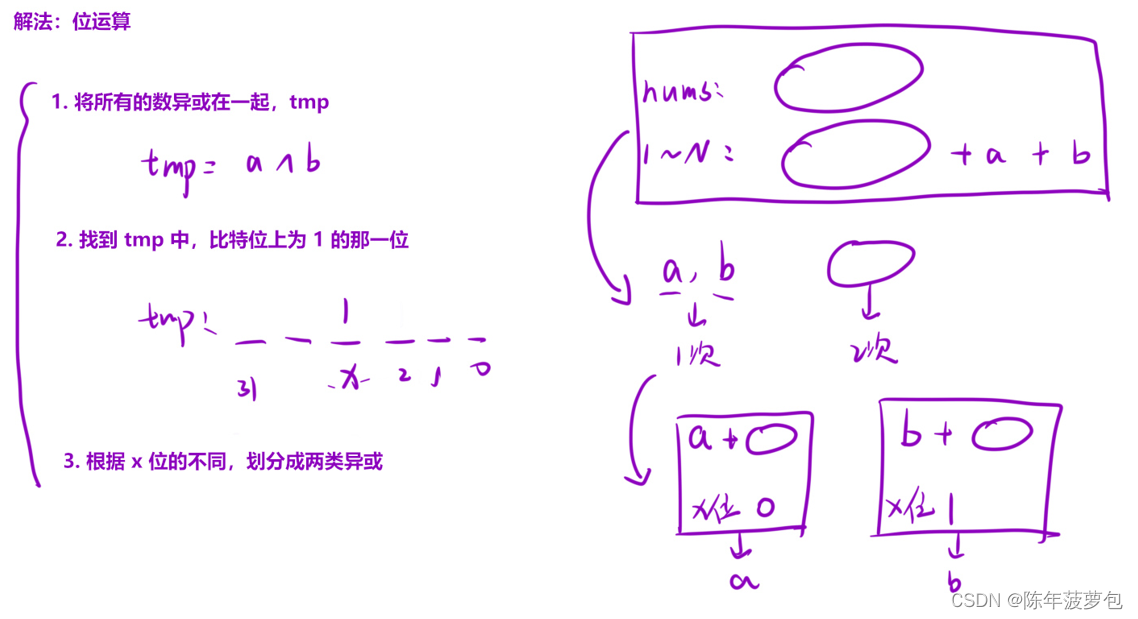
5.消失的两个数

  

class Solution {
public:
    vector<int> missingTwo(vector<int>& nums) 
    {
        vector<int> result;
        //将所有的数全部都异或到一起
        int tmp=0;
        int n=nums.size();
        for(auto ch:nums) tmp^=ch;
        for(int i=1;i<=n+2;i++) tmp^=i;
        //找到tmp中，比特位为1的那一位pos，在该比特位上a和b的比特值是不一样的。
        int pos;
        for(pos=0;pos<32;pos++) 
            if((tmp>>pos)&1) break;
        //根据pos位的不同，划分成为两类来异或
        int a=0,b=0;
        for(auto ch:nums)
        {
            if((ch>>pos)&1) a^=ch;
            else b^=ch;
        }
        for(int i=1;i<=n+2;i++)
        {
            if((i>>pos)&1) a^=i;
            else b^=i;
        }
        return {a,b};
    }
};

六、模拟算法

模拟算法就是依葫芦画瓢，思路比较简单，但是算法流程存在很多细节，将流程转换成为算法有比多要注意的细节。模拟题找优化一般都是通过找规律进行的。

6.替换所有的问号

class Solution {
public:
    string modifyString(string s) 
    {
        int n=s.size();
        //遍历字符串
        for(int i=0;i<n;i++)
        {
            //找到？字符
            if(s[i]=='?')
            {
                //遍历26个字母替换该字符
                for(char ch='a';ch<='z';ch++)
                {
                    //找到符合要求的字符，下面的if条件是关键
                    if((i==0 || ch!=s[i-1]) && (i==n-1 || ch!=s[i+1]))
                    {
                        s[i]=ch;
                        break;
                    }
                }
            }
        }
        return s;
    }
};

7.提莫攻击


 

class Solution {
public:
    int findPoisonedDuration(vector<int>& timeSeries, int duration) 
    {
        int result=0;
        for(int i=0;i<timeSeries.size()-1;i++)
        {
            if(timeSeries[i+1]-timeSeries[i]>=duration) result+=duration;
            else result+=(timeSeries[i+1]-timeSeries[i]);
        }
        return result+duration;
    }
};

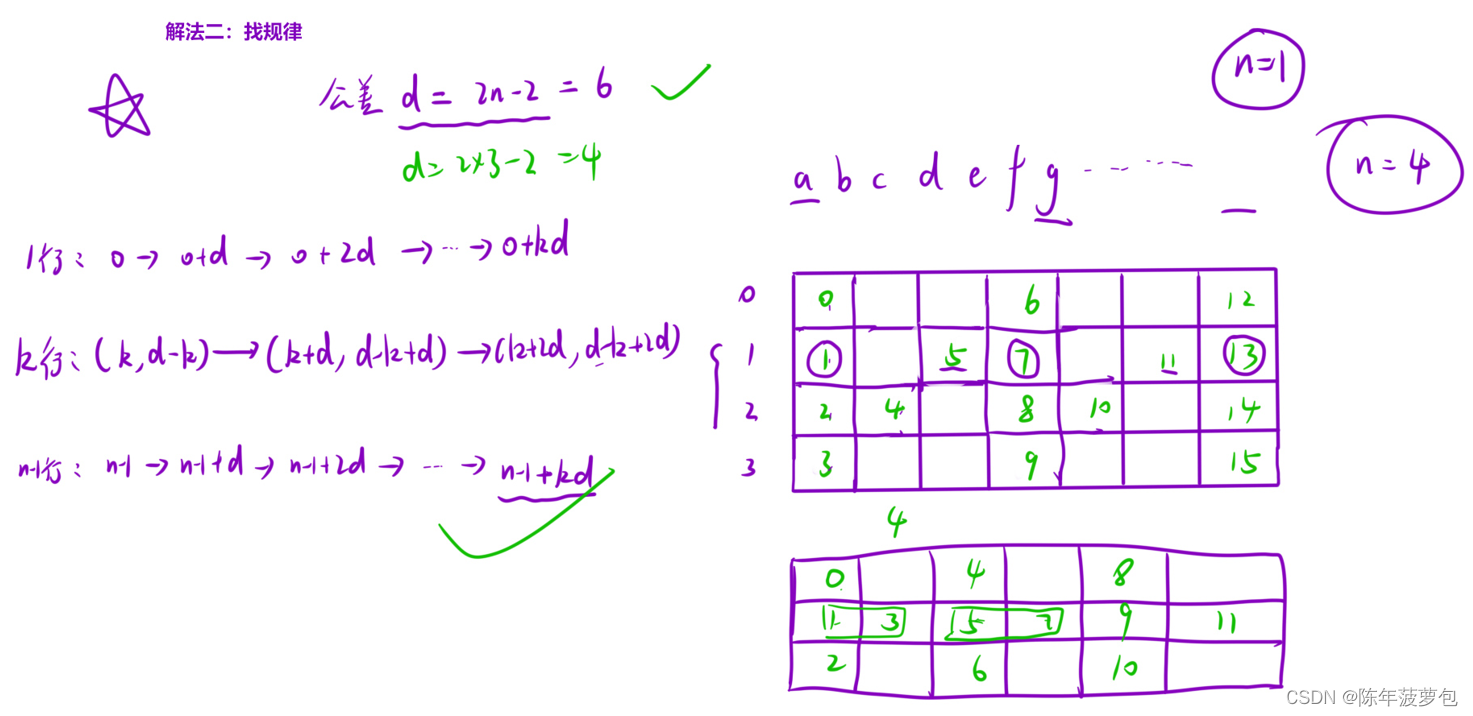
8.Z字形变换


class Solution {
public:
    string convert(string s, int numRows) 
    {
        //处理边界情况
        if(numRows==1) return s;
        string result;
        int n=s.size();
        int d=numRows*2-2;//公差d
        //1.先处理第一行
        for(int i=0;i<n;i+=d)
        {
            result+=s[i];//
        }
        //2.处理中间行
        for(int k=1;k<numRows-1;k++)//枚举每一行
        {
            for(int i=k,j=d-k;i<n || j<n;i+=d,j+=d)//注意不要将i<n || j<n写成了i<n && j<n
            {
                if(i<n) result+=s[i];
                if(j<n) result+=s[j];
            }
        }
        //3.最后处理最后一行
        for(int i=numRows-1;i<n;i+=d)
        {
            result+=s[i];
        }
        return result;
    }
};

9.外观数列

class Solution {
public:
    string countAndSay(int n) 
    {
        string result="1";
        if(n==1) return result;
        for(int i=1;i<n;i++)//翻译n次
        {
            string tmp;
            int len=result.size();
            //采用双指针来进行翻译
            for(int left=0,right=0;right<len;)
            {
                while(right<len && result[left]==result[right]) right++;//当right=len-1的边界情况也可以正确处理
                tmp+=to_string(right-left);//to_string函数处理下标left和right的值不同的时候
                tmp+=result[left];
                left=right;
            }
            result=tmp;
        }
        return result;
    }
};

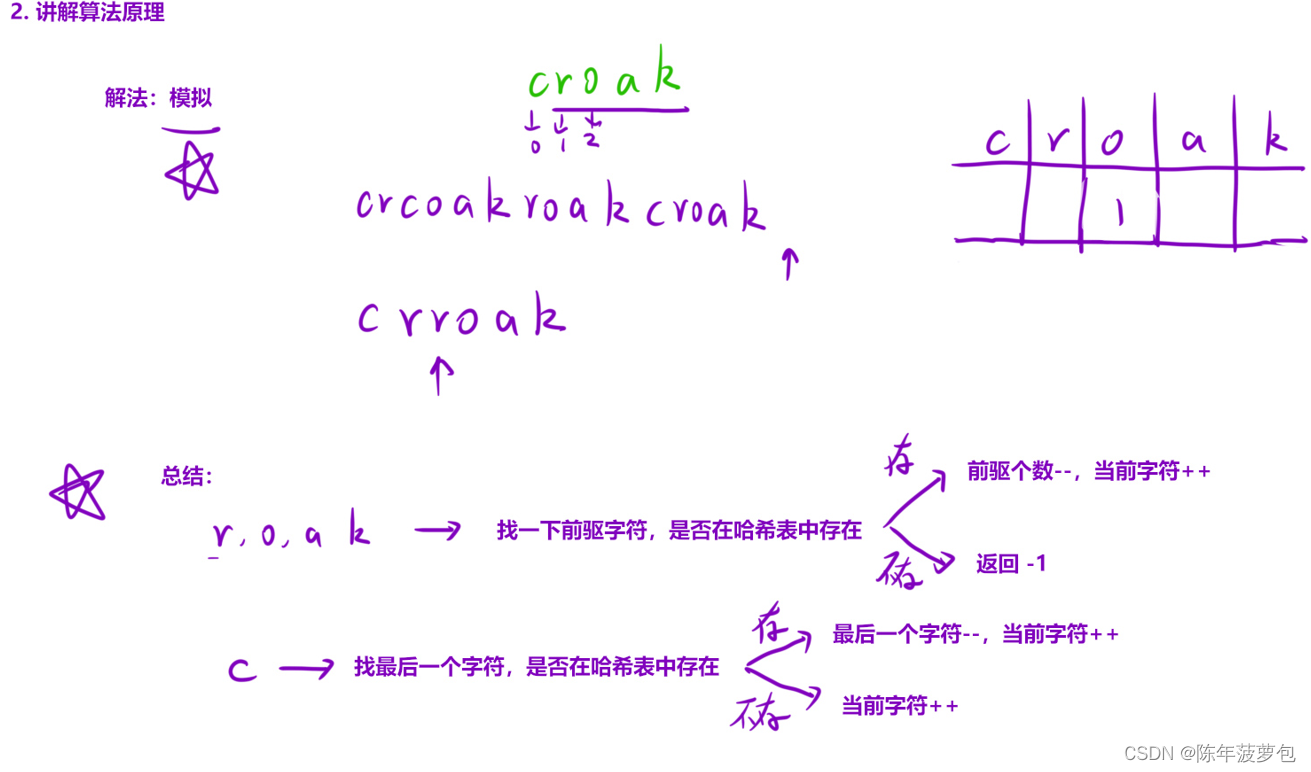
10.数青蛙


上述总结就是代码的逻辑非常重要

class Solution {
public:
    int minNumberOfFrogs(string croakOfFrogs) 
    {
        string t="croak";
        int n=t.size();
        vector<int> hash(n);//用数组来模拟哈希表
        unordered_map<char,int> index;//存储t字符串每个字符char以及对应的下标int
        for(int i=0;i<n;i++) index[t[i]]=i;
        //遍历字符串
        for(auto ch:croakOfFrogs)
        {
            //1、如果ch不在字符串t的范围内
            if(index.count(ch)==0) return -1;
            //2、如果字符ch不是c并且前面并没有匹配的字符
            if(ch!=t[0] && hash[index[ch]-1]<1) return -1;
            //3、正常运作
            if(ch==t[0] && hash[n-1]<1) hash[0]++;
            else if(ch==t[0] && hash[n-1]>=1) hash[0]++,hash[n-1]--;
            else hash[index[ch]]++,hash[index[ch]-1]--;
        }
        for(int i=0;i<n-1;i++) 
            if(hash[i]!=0) return -1;
        return hash[n-1];
    }
};

七、分治

分治就是分而治之，将一个大问题转换成为若干个相同或者相似的子问题，直到划分到子问题可以快速解决为止。

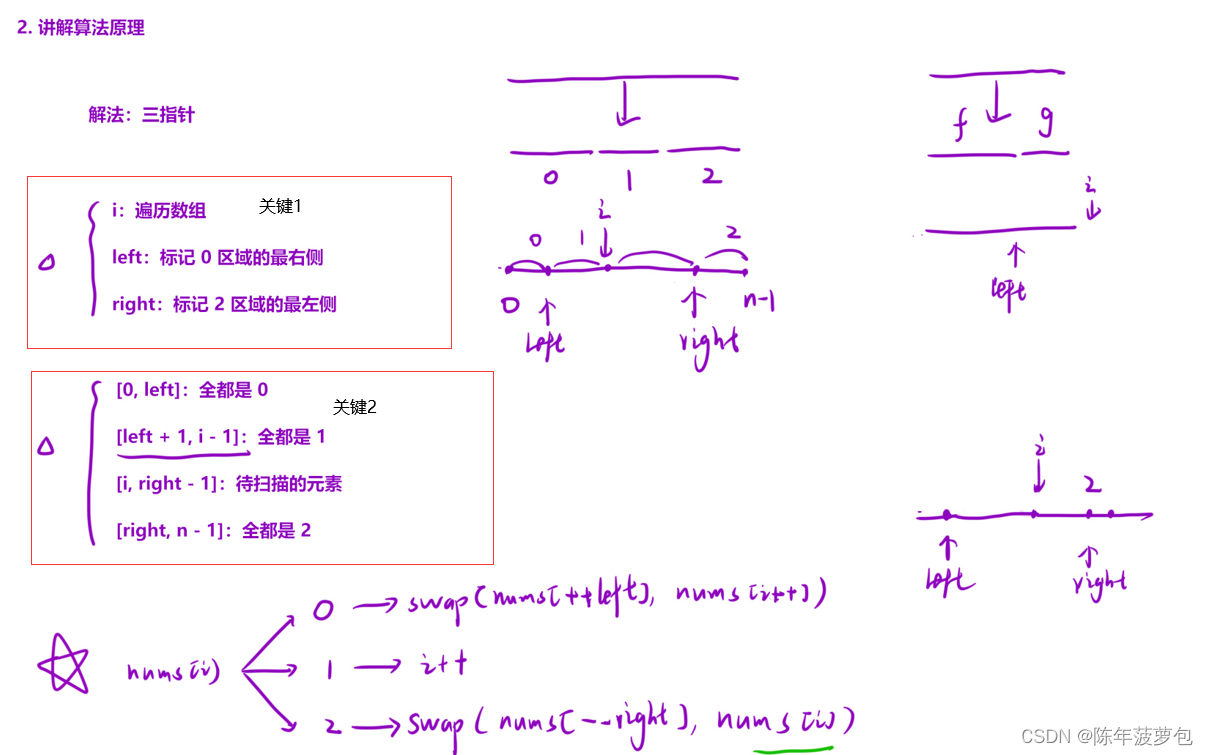
10.颜色分类(快排关键）


 

class Solution {
public:
    void sortColors(vector<int>& nums) 
    {
        int n=nums.size();
        int left=-1,right=n;
        for(int i=0;i<right;)//条件是i<right不是i<n，这是一个易错点。
        {
            if(nums[i]==0) swap(nums[++left],nums[i++]);
            else if(nums[i]==1) i++;
            else swap(nums[--right],nums[i]);
        }
    }
};

 11.排序数组 （快排）

class Solution {
public:
    int getrandom(vector<int>& nums,int left,int right)
    {
        int r=rand();
        return nums[r % (right-left+1) + left];
    }
    void sortArray_help(vector<int>& nums,int l,int r)
    {
        //定义递归出口
        if(l>=r) return;
        //随机方式选择基准元素
        int standar=getrandom(nums,l,r);
        int left=l-1;
        int right=r+1;
        //分成三块
        for(int i=l;i<right;)
        {
            if(nums[i]<standar) swap(nums[++left],nums[i++]);
            else if(nums[i]==standar) i++;
            else swap(nums[--right],nums[i]);  
        }
        sortArray_help(nums,l,left);
        sortArray_help(nums,right,r);
    }
    vector<int> sortArray(vector<int>& nums) 
    {
        srand(time(NULL));//种下一棵随机数种子
        sortArray_help(nums,0,nums.size()-1);
        return nums;
    }
};

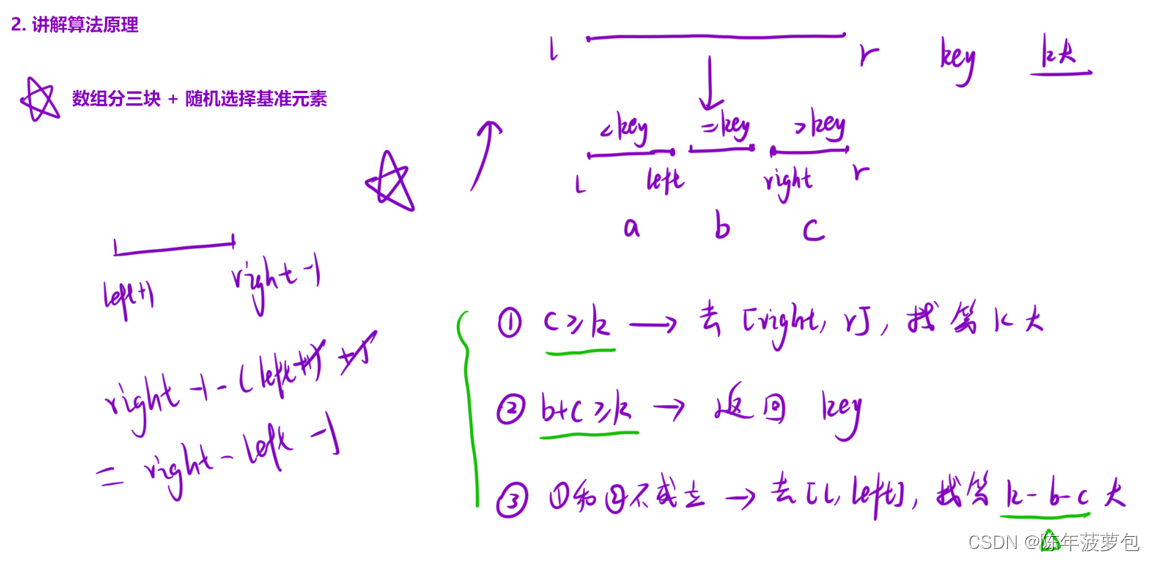
12.数组中的第k个最大元素

class Solution {
public:
    int getrandom(vector<int>&nums,int left,int right)
    {
        int r=rand();
        return nums[r%(right-left+1)+left];
    }
    int qsort(vector<int>& nums,int l,int r,int k)
    {
        if(l==r) return nums[l];//容易遗漏的点
        //1、随机选择基准元素
        int standard=getrandom(nums,l,r);
        //2、根据基准元素将数组分成三块
        int left=l-1;
        int right=r+1;
        int i=l;
        while(i<right)
        {
            if(nums[i]<standard) swap(nums[++left],nums[i++]);
            else if(nums[i]==standard) i++;
            else swap(nums[--right],nums[i]);
        }
        //分情况讨论
        //下面的三个条件判断是关键
        if(r-right+1>=k) return qsort(nums,right,r,k);
        else if(r-left>=k) return standard;
        else return qsort(nums,l,left,k-r+left);
    }
    int findKthLargest(vector<int>& nums, int k) 
    {
        srand(time(NULL));
        return qsort(nums,0,nums.size()-1,k);
    }
};

13.最小k个数（未做）

14.归并排序（归并排序）

class Solution {
public:
    vector<int> tmp;//辅助数组用来排序
    void mergesort(vector<int>& nums,int left,int right)
    {
        if(right<=left) return;
        //1、选择中间点划分区间
        int mid=(left+right)/2; 
        //2、将左右区间排序
        int left1=left;
        int right1=mid;
        int left2=mid+1;
        int right2=right;
        mergesort(nums,left1,right1);
        mergesort(nums,left2,right2);
        int i=0;
        //3、合并两个有序数组
        while(left1<=right1 && left2<=right2) tmp[i++]=nums[left1]<=nums[left2]?nums[left1++]:nums[left2++];
        //4、处理没有遍历完的数组
        while(left1<=right1) tmp[i++]=nums[left1++];
        while(left2<=right2) tmp[i++]=nums[left2++];
        //5、还原
        for(int i=left;i<=right;i++) nums[i]=tmp[i-left];     
    }
    vector<int> sortArray(vector<int>& nums) 
    {
        tmp.resize(nums.size());
        mergesort(nums,0,nums.size()-1);
        return nums;
    }
};

15.交易逆序对的总数（未做）

class Solution {
public:
    int reversePairs_helper(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;
        int ret=0;
        //1、找中间点，将数组分成两部分
        int mid=(left+right)>>1;
        //2.左边的个数+排序+右边的个数+排序
        ret +=reversePairs_helper(nums,left,mid);
        ret +=reversePairs_helper(nums,mid+1,right);
        //3.一左一右的个数
        int cur1=left,cur2=mid+1,i=0;
        vector<int> tmp(right-left+2);
        while(cur1<=mid && cur2<=right)
        {
            if(nums[cur1]<=nums[cur2]) tmp[i++]=nums[cur1++];
            else
            {
                ret+= mid-cur1+1;
                tmp[i++]=nums[cur2++];
            }
        }
        while(cur1<=mid) tmp[i++]=nums[cur1++];
        while(cur2<=right) tmp[i++]=nums[cur2++];
        for(int j=left;j<=right;j++)
            nums[j]=tmp[j-left];
        return ret;
      
    }
    
    int reversePairs(vector<int>& record) 
    {
        return reversePairs_helper(record,0,record.size()-1);
    }
};

16.計算右側小於當前元素的個數

class Solution {
    vector<int> ret;
    vector<int> index;//记录nums当前元素的下标、
    int tmpNums[500010];
    int tmpIndex[500010];
public:
    vector<int> countSmaller(vector<int>& nums) {
        int n=nums.size();
        ret.resize(n);
        index.resize(n);
        for(int i=0;i<n;i++)
            index[i]=i;
        mergesort(nums,0,nums.size()-1);
        return ret;
    }
    void mergesort(vector<int>& nums,int left,int right)  {
        if(left>=right) return;
        int mid=(left+right)>>1;
        mergesort(nums,left,mid);
        mergesort(nums,mid+1,right);
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid && cur2<=right)
        {
            if(nums[cur1]>nums[cur2])
            {
                tmpNums[i]=nums[cur1];
                ret[index[cur1]]+=right-cur2+1;
                tmpIndex[i]=index[cur1];
                i++;
                cur1++;
            }
            else
            {
                tmpNums[i]=nums[cur2];
                tmpIndex[i]=index[cur2];
                i++;
                cur2++;
            }
        }

        while(cur1<=mid)
        {
            tmpNums[i]=nums[cur1];
            tmpIndex[i]=index[cur1];
            i++;
            cur1++;
        }
        while(cur2<=right)
        {
            tmpNums[i]=nums[cur2];
            tmpIndex[i]=index[cur2];
            i++;
            cur2++;
        }
        for(int j=left;j<=right;j++)
        {
            nums[j]=tmpNums[j-left];
            index[j]=tmpIndex[j-left];
        }

       
    }
};

17.翻转对

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1863162.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android app Java层异常捕获方案

Android app Java层异常捕获方案

背景&#xff1a; 在Android app运行中&#xff0c;有时一些无关紧要的异常出现时希望App 不崩溃&#xff0c;能继续让用户操作&#xff0c;可以有效提升用户体验和增加业务价值。 新流程&#xff1a; 哪些场景需要Catch Crash Config配置信息&#xff1a; 支持从网络上获…
阅读更多...
MySQL 5.7.42 主从复制环境搭建

MySQL 5.7.42 主从复制环境搭建

MySQL 5.7.42 主从复制环境搭建 下载MySQL二进制包操作系统环境配置安装过程搭建从库 本次安装环境&#xff1a; OS版本&#xff1a;Red Hat Enterprise Linux Server release 6.8 (Santiago) MySQL版本&#xff1a;5.7.42 架构&#xff1a;同一台机器&#xff0c;多实例安装搭…
阅读更多...
国标GB28181视频汇聚平台EasyCVR安防监控系统常见播放问题分析及解决方法

国标GB28181视频汇聚平台EasyCVR安防监控系统常见播放问题分析及解决方法

国标GB28181安防综合管理系统EasyCVR视频汇聚平台能在复杂的网络环境中&#xff0c;将前端设备统一集中接入与汇聚管理。平台支持多协议接入&#xff0c;包括&#xff1a;国标GB/T 28181协议、GA/T 1400协议、RTMP、RTSP/Onvif协议、海康Ehome、海康SDK、大华SDK、华为SDK、宇视…
阅读更多...
【工具测评】ONLYOFFICE8.1版本桌面编辑器测评：好用！

【工具测评】ONLYOFFICE8.1版本桌面编辑器测评：好用！

随着远程工作的普及和数字化办公的发展&#xff0c;越来越多的人开始寻找功能强大、易于使用的办公软件。在这个背景下&#xff0c;ONLYOFFICE 8.1应运而生&#xff0c;成为许多用户的新选择。ONLYOFFICE 8.1是一款办公套件软件&#xff0c;提供文档处理、电子表格和幻灯片制作…
阅读更多...
【node】深入探讨 class URL

【node】深入探讨 class URL

【node】深入探讨 class URL &#x1f4cc; 浅说 fileURLToPath() 在vite.config.ts中有这么一段代码&#xff1a; import { fileURLToPath, URL } from node:url import { defineConfig } from vite export default defineConfig({resolve: {alias: {: fileURLToPath(new U…
阅读更多...
python学习笔记四

python学习笔记四

1.自己平方本身 x2 x**4#xx**4 print(x) 2.把一个多位数拆分成单个数&#xff0c;方法一通过字符串下标获取对应元素&#xff0c;并对获取的元素使用eval函数把左右引号去掉&#xff0c;是字符串变为整型&#xff1b;方法二&#xff0c;通过对数进行取余和整除得到各个位的数 …
阅读更多...
RK3568平台开发系列讲解（I2C篇）利用逻辑分析仪进行I2C总线的全面分析

RK3568平台开发系列讲解（I2C篇）利用逻辑分析仪进行I2C总线的全面分析

🚀返回专栏总目录 文章目录 1. 基础协议1.1. 协议简介1.2. 物理信号1.3. 总线连接沉淀、分享、成长，让自己和他人都能有所收获！😄 1. 基础协议 1.1. 协议简介 IIC-BUS（Inter-IntegratedCircuit Bus）最早是由PHilip半导体（现在被NXP收购）于1982年开发。 主要是用来方…
阅读更多...
安卓应用开发学习：获取导航卫星信息

安卓应用开发学习：获取导航卫星信息

一、引言 我昨天写了《安卓应用开发学习&#xff1a;获取经纬度及地理位置描述信息》日志&#xff0c;今天再接再厉&#xff0c;记录一下跟着《Android App 开发进阶与项目实战》一书&#xff0c;实现获取导航卫星信息&#xff0c;并在手机上显示的功能的情况。先上实现后的在…
阅读更多...
go语言day2 配置

go语言day2 配置

使用cmd 中的 go install &#xff1b; go build 命令出现 go cannot find main module 错误怎么解决&#xff1f; go学习-问题记录(开发环境)go: cannot find main module&#xff1b; see ‘go help modules‘_go: no flags specified (see go help mod edit)-CSDN博客 在本…
阅读更多...
FPGA学习笔记（6）——硬件调试与网表添加探针

FPGA学习笔记（6）——硬件调试与网表添加探针

对信号进行分析&#xff0c;除了使用内置的ILA IP核&#xff0c;还可以在网表中添加探针。 本节采用之前配置的LED灯闪烁代码&#xff0c;对原始工程进行修改。 如果是新建工程&#xff0c;需要现将代码进行综合Synthesis&#xff0c;然后再进行接下来的操作。 1、点击Open S…
阅读更多...
链表数组遍历输出的辨析（二者都含指针的情况下）----PTA期末复习题

链表数组遍历输出的辨析（二者都含指针的情况下）----PTA期末复习题

输入输出三位学生的学号和信息 一开始我认为是指针&#xff0c;直接背了指针输出的方式&#xff1b;p;p!NULL;pp->next 这个是错误的 下面这个输出是正确的方式 分析怎么区分这两个 举个例子来 数组遍历&#xff1a; 链表遍历&#xff1a; 输出的结果&#xff1a; 如果将…
阅读更多...
浏览器扩展V3开发系列之 chrome.cookies 的用法和案例

浏览器扩展V3开发系列之 chrome.cookies 的用法和案例

【作者主页】&#xff1a;小鱼神1024 【擅长领域】&#xff1a;JS逆向、小程序逆向、AST还原、验证码突防、Python开发、浏览器插件开发、React前端开发、NestJS后端开发等等 chrome.cookies API能够让我们在扩展程序中去操作浏览器的cookies。 在使用 chrome.cookies 要先声明…
阅读更多...
【Redis】Zset有序集合常用命令以及使用场景

【Redis】Zset有序集合常用命令以及使用场景

Redis 的有序集合&#xff08;Sorted Set&#xff0c;简称 Zset&#xff09;是一个非常强大的数据结构&#xff0c;它结合了集合&#xff08;Set&#xff09;的唯一性和列表&#xff08;List&#xff09;的有序性。每个元素都关联一个评分&#xff08;score&#xff09;&#x…
阅读更多...
减少液氮罐内液氮损耗的方法

减少液氮罐内液氮损耗的方法

监测与管理液氮容器的密封性能 液氮容器的密封性能直接影响液氮的损耗情况。一个常见的损耗源是容器本身的密封不良或老化导致的泄漏。为了有效减少液氮损耗&#xff0c;首先应当定期检查液氮容器的密封性能。这可以通过简单的方法如肉眼检查外观&#xff0c;或者更精确的方法…
阅读更多...
SEO与AI的结合：如何用ChatGPT生成符合搜索引擎优化的内容

SEO与AI的结合：如何用ChatGPT生成符合搜索引擎优化的内容

在当今数字时代&#xff0c;搜索引擎优化&#xff08;SEO&#xff09;已成为每个网站和内容创作者都必须掌握的一项技能。SEO的主要目标是通过优化内容&#xff0c;使其在搜索引擎结果页面&#xff08;SERP&#xff09;中排名更高&#xff0c;从而吸引更多的流量。然而&#xf…
阅读更多...
嵌入式学习——硬件（ARM体系架构）——day51

嵌入式学习——硬件（ARM体系架构）——day51

1. S3C2440基础知识——一条指令四个字节 1.1 定义 S3C2440 是三星&#xff08;Samsung&#xff09;公司设计的一款基于 ARM920T 核心的微处理器&#xff0c;广泛应用于嵌入式系统中&#xff0c;属于三星的 S3C24xx 系列。 1.2 处理器核心 ARM920T&#xff1a;基于 ARM v5T …
阅读更多...
[C#][opencvsharp]C#使用opencvsharp进行年龄和性别预测支持视频图片检测

[C#][opencvsharp]C#使用opencvsharp进行年龄和性别预测支持视频图片检测

使用 OpenCVSharp 来调用 age_net.caffemodel 和 gender_net.caffemodel 来进行性别和年龄预测涉及几个步骤。以下是一个简化的流程和示例文案&#xff1a; 1. 准备工作 确保你已经安装了 OpenCVSharp 和相关的依赖项。确保你有 age_net.prototxt、age_net.caffemodel、gende…
阅读更多...
市面上很轻的 100kW 负载组

市面上很轻的 100kW 负载组

FX100S-C 负载组 EAK的 FX100S-C 负载组在轻质外壳中以 415Vac 50Hz 提供 100kW 的连续负载。数字仪表允许您测量功率、电压、电流和频率&#xff0c;同时还允许您在进行测试时记录数据。 EAK是市场上最轻的 100kW 负载组之一&#xff0c;它将使您能够访问其他负载组无法到达…
阅读更多...
离线部署OpenIM

离线部署OpenIM

目录 1.提取相关安装包和镜像 2.安装docker和docker-compose 3.依次导入镜像 4.解压安装包 5.执行安装命令 6.PC Web 验证 7.开放端口 7.1IM 端口 7.2Chat 端口 7.3 PC Web 及管理后台前端资源端口 “如果您在解决类似问题时也遇到了困难&#xff0c;希望我的经验分享…
阅读更多...
服务运营 | MS文章精选：线上点单，当真免排队？餐饮零售与医疗场景中的全渠道运营

服务运营 | MS文章精选：线上点单，当真免排队？餐饮零售与医疗场景中的全渠道运营

编者按&#xff1a; 小A走进了一家奶茶店&#xff0c;准备向店员点单&#xff0c;但却在屏幕上看到还有98杯奶茶待制作&#xff08;因为线上订单突然暴增&#xff09;。因此&#xff0c;小A不满地嘟囔着离开了奶茶店。这个例子展示了线上渠道可能会对线下渠道造成一些负面影响…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023