编者按：

小A走进了一家奶茶店，准备向店员点单，但却在屏幕上看到还有98杯奶茶待制作（因为线上订单突然暴增）。因此，小A不满地嘟囔着离开了奶茶店。这个例子展示了线上渠道可能会对线下渠道造成一些负面影响。事实上，许多奶茶品牌，例如奈雪的茶、喜茶与CoCo等都提供云点餐服务，它们打出标语“手机点单免排队”，虽然这种模式直觉上可以增加消费者福利减少排队，但实际不然。在本次推文中，我们将重点放在零售餐饮与医疗这三个行业的线上与线下双渠道上。它们有时可以是相辅相成的关系，但有时也可能形成对立（正如我们刚提到的例子）。我们此次分享的论文均来自于MS，这些论文分别关注这三个行业全渠道运营中的如下几个问题：

1. 第一篇论文的现实灵感源于餐饮行业中手机点单免排队的服务模式。作者使用排队论的方法探讨了单一渠道和全渠道服务下的特点。作者指出线上点单模式可能对消费者福利构成潜在危害，并进一步讨论了各种补救措施对全渠道服务的优化效果。
2. 第二篇论文的现实灵感源自零售业中的快闪店这一营销策略。作者与阿里巴巴合作，在天猫平台上进行了一场大型田野实验。实验旨在分析快闪店这一线下营销模式如何通过间接途径影响线上零售。
3. 第三篇论文的现实灵感源于医疗场景中线上预约就诊患者与未预约患者之间的冲突。作者设计了一个随机优化模型来研究全渠道模式（预约就诊、未预约就诊）下的医疗预约时间表的设计问题。

Omnichannel Services: The False Premise and Operational Remedies

Problem
全渠道运营（线上点单（online channel），线下取货（walk-in channel））的发展趋势正在蓬勃发展。在这种模式下，顾客可以提前在线上下单，然后在线下店铺取货，这可以大大缩短顾客排队等待的时间。这种模式已经在餐饮行业如星巴克、麦当劳以及精品店如Skip等开始推行。然而，尽管这种模式可以增加服务提供商的利润，但也可能会影响线下顾客的个人体验，从而导致社会福利和吞吐量的减少。此外，现实中存在多种服务模式，如先到先服务、渠道监管、渠道专用、优先渠道顾客等。然而，在现有研究中，对于这些模式下企业利润、消费者体验、社会福利和排队系统吞吐量的理论分析相对较少。为了探讨各种模式的最佳运用场景，本文运用排队论研究了全渠道服务模式下的决策问题。
Method
作者采用M/M/1模型来设计整篇文章的排队问题，首先，作者建立”先来先服务模型“（first-come first-served model），写出walk-in channel和online channel下的消费者效用函数：

$$U_w=\sum _{i=0}^{n-1}{p}_i\cdot \left(R-c_w\frac{i+1}{\mu }\right)-T$$
$$U_o=\sum _{i=0}^{\infty }{p}_i\cdot \left(R-c_o\frac{i+1}{\mu }\right)-T$$
其中， $U_w$中的${\sum }_{i=0}^{n-1}$则代表了累加从队列中没有任何顾客（$i=0$）至有$n-1$个顾客等待的情形，表示是为了计算从队列中无顾客等待到$n-1$个顾客等待时的总效用；而$U_o$中的${\sum }_{i=0}^{\infty }$则代表了线上渠道信息不透明（手机线上点单时不会提示用户前方有多少人等待，或者说只有成功付款后手机上才显示前方的等待人数）导致在线点单者点完单就必须等待的情形（看不见的等待）。当根据M/M/1的系统稳定状态的条件（公式1），写出系统稳态（公式2）下的顾客进入系统的概率$p_i$是online customer（OC）比例$\gamma$的函数$p_i(\gamma )$，即进而得出全渠道稳定状态下的一个重要特性，即，在稳定的全渠道系统中，OC的预计停留时间随着OC的人数比例严格递增。
$$\begin{array}{c}\lambda P_i=\mu P_{i+1}\end{array}$$

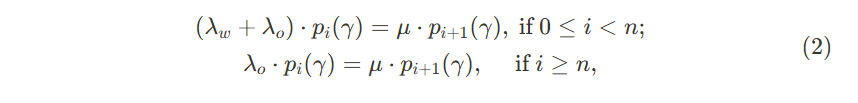
得出稳态条件后，作者定义系统产出system throughput($TH(\gamma )$)和社会福利social welfare($S(\gamma )$)，并以Naor (1969)的传统walk-in系统作为本文全系统下（$\gamma$=0）的benchmark，写出该情景下的$TH(\gamma )$，$S(\gamma )$和$U$。之后，作者得出渠道均衡决策（即顾客在两种渠道之间的选择无差异），该决策与单位等待成本密切相关。

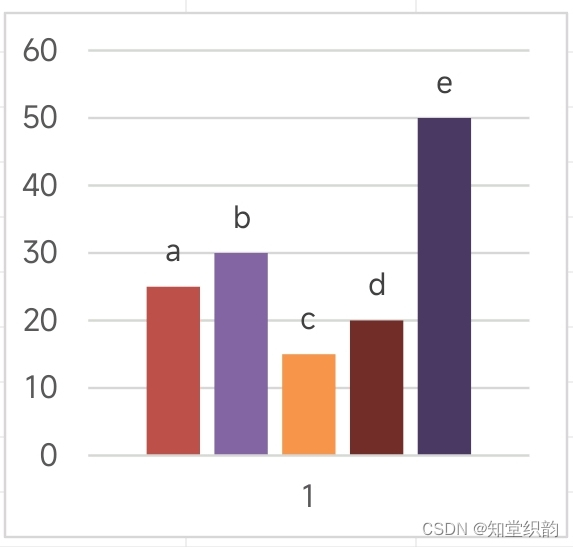
下图展示了顾客在不同的在线单位等待时间和交通强度下的渠道选择偏好。该结果揭示：只要在线单位等待成本相对于现场等待成本足够小，顾客总是以一定的概率选择在线渠道。

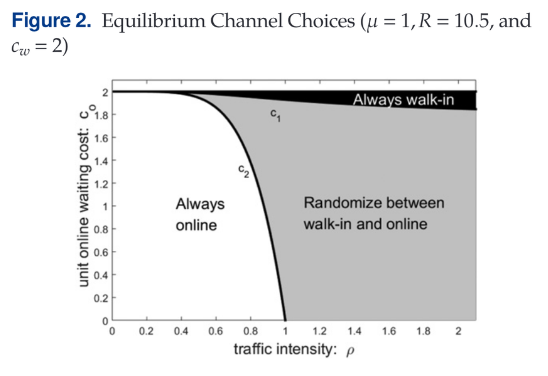
紧接着，作者探讨了全渠道服务下的影响，根据以上得出的均衡结果探讨纯线下模式（all-walk-in 均衡），纯线上模式（all-online 均衡）以及全渠道模式（omni均衡）。主要结论表明，引入较低单位等待成本的online channel确实提高了系统产出TH，然而却有益或损害客户的个人效用和社会福利，具体取决于均衡渠道选择，这导致在线渠道的引入在各利益方之间产生分歧。

对此，作者在后面一章第一节探讨了现有的全渠道系统的运营补救措施，即，行业最先进技术的影响。第一项是在线监管（Online-Channel Regulations），即，限制使用在线渠道，包括限制线上顾客下单时间即，设${\theta }_i$为顾客下单被接受的概率，$1-{\theta }_i$为顾客下单被拒绝的概率，此时的系统稳定状态条件为：

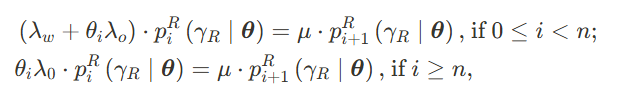
在该稳定状态及均衡结果下，作者探讨了监管者是否对online customer揭露实时队伍信息,主要结果表明，当单位等待时间低于某一阈值时，不揭露队伍信息（unobservable）时全渠道服务的总产量不少于揭露队伍信息（observable）的在线服务渠道的吞吐量。
第二个方法为战略延迟（strategic delay），设$d_i$为SD时间，此时线上渠道和线下渠道的消费者效用为：

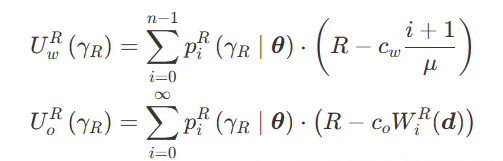
该情况下没有封闭解析解，然而数值算例表明该情况下的结论和benchmark下的结论一致，该均衡决策与单位等待成本密切相关。

之后，作者在该章第二节探讨了现实中已有的另一种运营模式：渠道专用全能系统（Channel-Dedicated Omni-Systems），即服务提供商分出一部分capacity专门服务online customer，作者将线上和线下渠道服务设为两个单独的queuing system，进行计算，得出主要结论为，即使将容量分割后降低了容量效率，但渠道专用系统下的吞吐量不一定比仅步入式下的吞吐量低；对于低流量的系统，容量分配不仅可以抵消奉献带来的效率损失，还可以吸引更多的在线订单以获得更大的吞吐量。紧接着，作者在下面一章节又探讨了以线下顾客为优先（Prioritization for walk-in customer）的补救措施，主要结论为优先级全系统可以提供全渠道技术，在传统的步入式系统的基础上同时提高提供商的收入和客户体验，然而整个系统的吞吐量可能会收到影响。

Results

1. 作者发现全渠道模式下，渠道均衡决策（即顾客在两种渠道之间的选择无差异），与线上渠道的单位等待成本密切相关。
2. 当两种渠道均衡使用时，在线订购会无意中降低顾客的个人效用和社会福利。而且网上订购和等待的成本越少，社会福利减少得越多。
3. 尽管两种补救措施都可以提高walk-in only和the first-come-first-served omnichannel service的吞吐量，但它们不太可能在不损害社会福利的情况下实现这一目标。
   Why recommend?
   本文使用排队论探讨了全渠道模式下的运营优化问题，首先对比了仅线上、仅线下和全渠道下的均衡决策，之后探讨了服务提供商的服务模式，得出普适结论，即该模式无法兼顾服务提供商利润、社会福利、吞吐量和消费者效用。为此，作者探讨了一些补救措施，包括线上监管、线上渠道专用、优先线下顾客服务等措施，并得出各情景下的服务提供商利润、社会福利、吞吐量和消费者效用，并为每种情景下的参数阈值进行了探讨。该文章有助于读者从排队论的角度思考现有商业模式的转换情况。

The Value of Pop-Up Stores on Retailing Platforms: Evidence from a Field Experiment with Alibaba Problem

电商的红利似乎已陷入瓶颈，快闪店作为一种新的营销模式可以将线下流量进一步引流到线上。许多奢侈品牌和一些年轻品牌或公司都热衷于快闪店，例如泡泡玛特、LVMH、茶颜悦色与哔哩哔哩等。作为一种短期的营销活动，品牌方可以利用人工智能、VR等新兴技术与创意性的装修风格在线下带给消费者切身的新鲜感，拉近消费者与品牌方的距离，提升品牌认知。《中国快闪店行业白皮书》指出快闪店的交易规模在2020-2025年均复合增速约为21.1%。本文与阿里巴巴合作，在天猫平台上进行了一场大型的田野实验，分析快闪店这一线下营销模式如何间接地影响线上零售。

Method
随机田野实验的背景是2017年10月12日至19日阿里巴巴在杭州推出的一家快闪店。此次快闪店囊括了天猫平台上售卖牛仔裤的四家服装品牌。同时本次快闪店融合了一些智能化技术，例如，“云货架”，消费者只需拿着牛仔裤放在云货架前，其屏幕就会自动显示产品的详细信息；另外一个是“虚拟试衣间”，消费者可以根据此项功能进行虚拟换装。

参与实验的人共计799904人，这些人均有淘宝账号，且居住在快闪店线下地址的10千米范围内。这些人被随机分为两组，实验组与控制组。2017年10月12日早，实验组的受试者会收到快闪店活动的短信（短信内容如下图所示），但控制组不会。

整个数据收集的过程分为三个阶段：

1. 快闪店活动前的三个星期（2017年9月21日至10月11日）；
2. 快闪店活动的一个星期（2017年10月12日至19日）；
3. 快闪店活动后的六个星期（2017年10月20日至11月30日）。

收集的数据主要包括这些时段内消费者在天猫平台上的支出数据。阿里巴巴采用了先进的wifi技术可以识别用户是否参与了线下的快闪店活动，通过这种技术，作者就可以识别在快闪店活动前后，消费者在进行线上天猫消费时，哪些消费者曾经参与了线下快闪店活动。注意，这种技术存在一些限制，它无法识别搭载iOS 7以上版本的苹果手机，因此无法收集苹果用户的数据。因此，作者专注于分析安卓手机用户的数据。
Results
推送快闪店动态对消费者行为的影响
此时，相应的回归方程如下，
$${\text{Average Daily Expenditure for Participating Retailers}}_i={\delta }_0+{\delta }_1{\text{Treatment}}_i+{ϵ}_i,$$
其中，${\text{Treatment}}_i$为一个二元变量，如果消费者$i$收到了快闪店活动消息，${\text{Treatment}}_i$为1，否则为0，${\text{Average Daily Expenditure for Participating Retailers}}_i$为消费者$i$的平均每日支出。经统计检验，作者发现为消费者推送快闪店动态，可以增加消费者参与快闪店活动的可能性。同时，作者发现实验组中的消费者在发送消息当天比快闪店活动前在天猫平台上的平均每日花费多0.007元（是统计显著的）。

参与快闪店活动对消费者行为的影响
此时，作者采用两阶段最小二乘回归，回归方程如下：
$${\text{Average Daily Expenditure for Participating Retailers}}_i={\alpha }_0+{\alpha }_1{\text{Visit}}_i+{ϵ}_i,$$
$${\text{Visit}}_i={\beta }_0+{\beta }_1{\text{Treatment}}_i+{ϵ}_i,$$
其中，${\text{Visit}}_i$为一个二元变量，当消费者$i$参与了快闪店活动（被wifi技术检测到参与了快闪店活动），${\text{Visit}}_i$为1，否则为0。统计结果显示，参与线下快闪店活动的消费者比不参加的消费者在天猫平台上平均每日多支出2.05元。

Why recommend？
快闪店作为一种流行的营销方式被许多品牌所推行。本文在田野实验中使用了先进的wifi技术来考察线下快闪店对线上消费支出的影响，证明了快闪店对促进虚拟经济的积极影响。考虑天猫平台没有自己的实体店铺，作者因此建议天猫平台将快闪店作为一项重要的线下渠道来促进消费。

Managing Appointment-Based Services in the Presence of Walk-in Customers

Problem
“预约就诊”已成为如今大型门诊就医的主流方式。患者可以先进行线上预约挂号，依据预约时间再到实体医院看病。然而，也存在一些患者没有进行网上预约，直接到医院就医，我们把这类患者称之为 Walk-in Customers（未预约患者）。在美国的初级医疗保健中，10%~60%的患者都属于Walk-in Customers，他们组成了一个重要的患者流。以往的研究在设计预约时间表时很少考虑Walk-in Customers，然而忽略这部分群体可能在实践中导致患者过长的等待时间和医护人员的加班，使整个就医效率下降。考虑到Walk-in Customers具有较强的不确定性，这为预约时间表的设计带来挑战，作者设计了一个随机优化模型来解决这一问题。特别地，假如有$T$个时段与$n$个预约患者，在考虑Walk-in Customers随机到达医院就医的基础下，每个时间段 t ∈ { 1 , 2 , . . . , T } t \in \{1,2,...,T\} t∈{1,2,...,T}应安排多少位预约患者$x_t$就医（$n={\sum }_{t=1}^T{x}_t$）？

Method
在设计预约时间表时，作者希望最小化成本$(C_S{\Gamma }_S+C_W{\Gamma }_W+C_I{\Gamma }_I+C_O{\Gamma }_O)$，其中$C_S$和$C_W$分别表示预约患者和Walk-in Customer单位等待时间的成本，${\Gamma }_S$和${\Gamma }_W$分别表示预约患者和Walk-in Customer的预期等待时长；$C_I$和$C_O$分别表示医生单位空闲时间和加班时间的成本，${\Gamma }_I$和${\Gamma }_O$分别表示医生空闲和加班的预期时长。因此，作者的目标函数是最小化患者等待、医生空闲及加班造成的总成本。

假设医生为每一个患者接诊的时长恰好花费一个时间段（虽然每位患者的就诊时间需花费一个时段，但每个时段允许接收多个患者的预约）。记${\Gamma }_D$为医生开始提供服务到最后一个患者离开医院所花费的时间。因此，${\Gamma }_O={\Gamma }_D-T$。记${\beta }_t$为第$t$个时间段内Walk-in Customer的数量（被定义为随机变量），则 N W = E { ∑ t = 1 T β t } N_W=\mathbb{E}\{\sum_{t=1}^T \beta_t\} NW​=E{∑t=1T​βt​}为预期Walk-in Customer的总数。于是有，${\Gamma }_I={\Gamma }_D-{\sum }_{t=1}^T{x}_t-N_W$。记$C_D=C_I+C_O$，且不失一般性，令$C_S=1$。于是目标函数简化为
$${\Gamma }_S+C_W{\Gamma }_W+C_D{\Gamma }_D-C_I\sum _{t=1}^T{x}_t.$$
为计算${\Gamma }_S$，${\Gamma }_W$和${\Gamma }_D$，作者首先计算${\Pi }_t(k)$，意为有$k$个患者在第$t$个时段结束时还在等待就医。记$p_t(b)$为 $b$个Walk-in Customers在第$t$个时间段到达（相当于$p_t(b)=Pr({\beta }_t=b)$）。于是${\Pi }_t(k)$通过计算联合概率有如下递归方程
$$\begin{array}{rl}{\Pi }_t(k)& =\sum _{j=0}^{k-x_t+1}{\Pi }_{t-1}(j)p_t(k-x_t-j+1)\\ & +\{\begin{array}{cc}{\Pi }_{t-1}(0)p_t(0)& \text{if }k=0\mathrm{and}{x}_t=0,\\ 0& \text{otherwise}\end{array}\end{array}$$
记${\bar{N}}_t$为一个较大的数（可以被视为Walk-in Customer在$t$时段的分布在${\bar{N}}_t$这个位置进行截断）。于是有
$\Gamma_D=T+\sum_{k=1}^{\overline{N_T}}k\Pi_T(k), $
上式右侧的第二项表示在第$T$个时段结束时，还在等候的患者数量的期望。记$s_t$为第$t$个时段结束时还在等候的预约患者数量，于是有递归方程$s_t=(s_{t-1}+x_t-1{)}^{+}$，进一步有
$${\Gamma }_S(\mathbf{x})=\sum _{t=1}^T{s}_t+\sum _{j=1}^{s_T-1}j.$$
且所有患者等待的预期总时长为
$${\Gamma }_T(\mathbf{x})=\sum _{t=1}^T\sum _{k=1}^{\overline{N_t}}k{\Pi }_t(k)+\sum _{k=1}^{\overline{N_T}}\left(\sum _{j=1}^{k-1}j\right){\Pi }_T(k).$$
因此，Walk-in Customers的总等候时长为
$${\Gamma }_W(\mathbf{x})={\Gamma }_T(\mathbf{x})-{\Gamma }_S(\mathbf{x}).$$
作者发现目标函数$${\Gamma }_S+C_W{\Gamma }_W+C_D{\Gamma }_D-C_I\sum _{t=1}^T{x}_t$$具有Multimodularity的性质，这种性质使得局部最优解就是全局最优解。以上的讨论均假设预约患者会按时到医院就诊，没有违约。作者在后续进一步考虑了预约患者会违约时的模型，并设计了一种约束生成算法来进行求解。

Results

1. 作者发现考虑Walk-in Customers的预约时间表与不考虑Walk-in Customers的预约时间表存在非常明显的差异。由于Walk-in Customers的随机性，在设计预约时间表时，一些时段应该空着。
2. 即使考虑预约患者违约的可能，最优的时间表也可能存在在部分时段超额预定的情况。尽管如此，由于Walk-in Customers的不确定性，最优时间表里仍然有部分时段为空缺的可能。也就是说，在同一张最优时间表里，部分时段允许超额预定，部分时段不安排预约患者。Walk-in Customers不能抵消违约的影响。
3. 作者还使用真实的医院运营数据来验证所提方法的有效性。作者发现，当医院切换到作者所提的时间表时，成本会降低42%-73%。

Why recommend？
本文率先考虑了Walk-in Customers情形下的预约时间表设计，以期最小化患者与医生的时间成本。特别是在中国，虽然患者预约挂号的习惯在近些年被逐渐养成，但相关数据显示，截至2023年11月，全国三级门诊的平均线上预约率为49.2%，这意味着约一半的患者均为Walk-in Customers。因此，作为一项重要的不确定因素，考虑Walk-in Customers的预约时间表设计显得非常重要。不仅如此，本文的建模框架具有良好的扩展性，可以运用在其它领域的预约问题中。