计算机图形学 第5章 二维变换与裁剪到Cohen-Sutherland直线裁剪算法

news2024/9/29 11:40:08

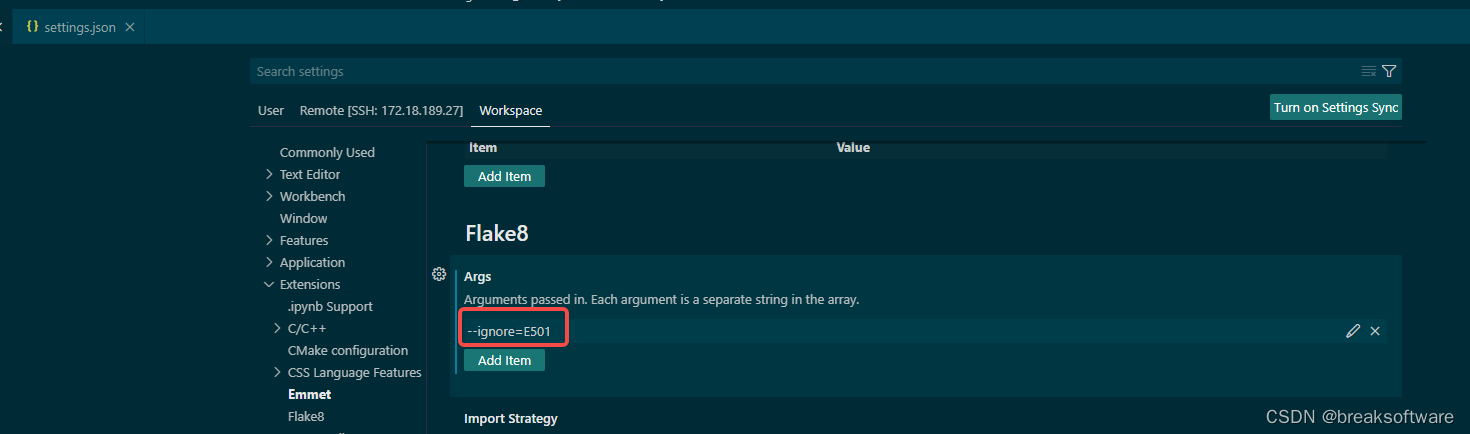
目录

  • 学习目标
  • 前驱知识
    • 规范化齐次坐标
    • 二维几何变换矩阵
    • 物体变换与坐标变换
    • 二维几何变换
    • 二维图形基本几何变换矩阵
      • 平移变换矩阵
      • 比例变换矩阵
      • 旋转变换矩阵
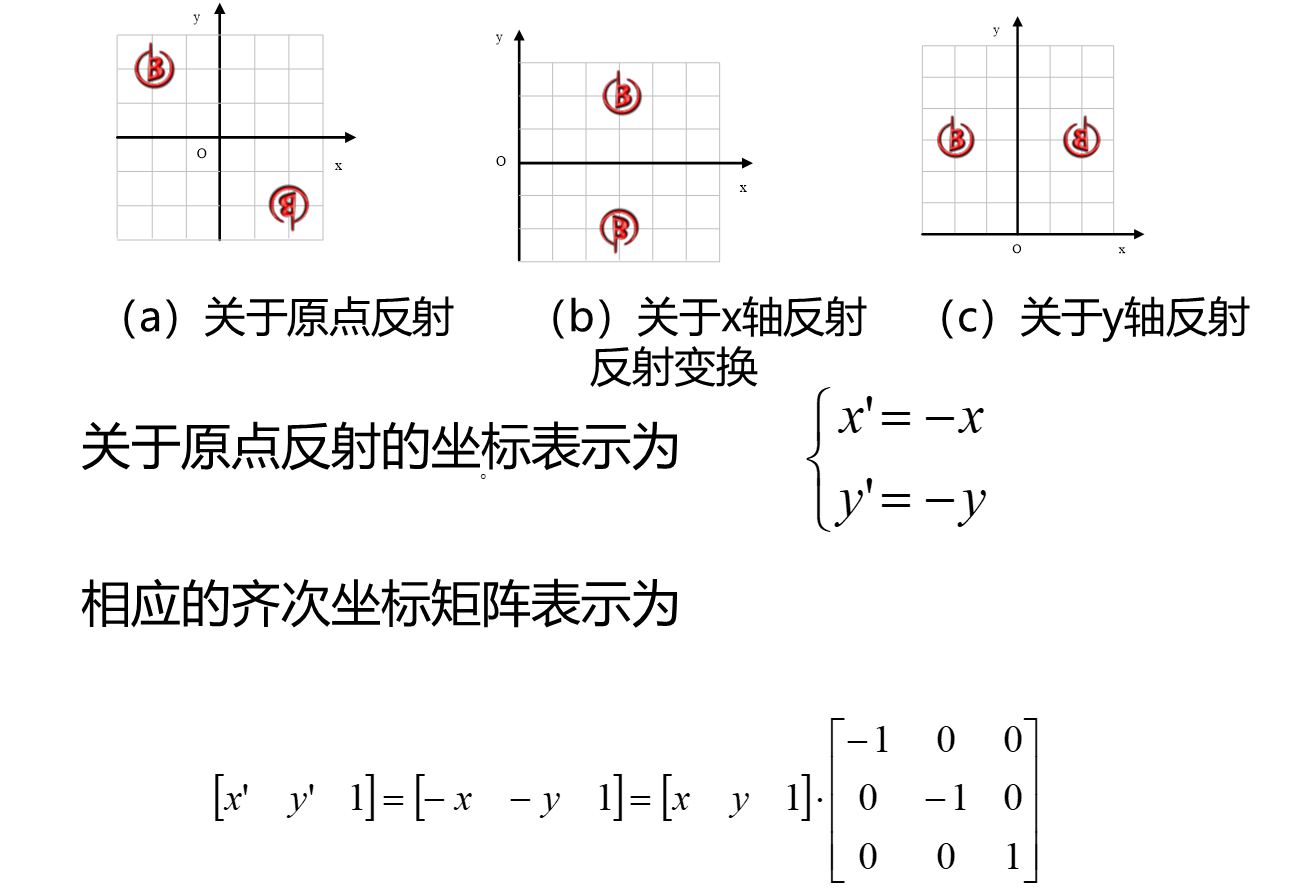
      • 反射变换矩阵
      • 错切变换矩阵
    • 二维仿射变换
  • 二维复合变换
    • 相对于任意方向的二维几何变换
  • 二维图形裁剪
    • 世界坐标系
    • 2.用户坐标系
    • 观察坐标系
    • 屏幕坐标系
    • 设备坐标系
    • 窗口与视区
      • 窗视变换矩阵
  • 裁剪算法
    • Cohen-Sutherland直线裁剪算法（科恩-萨瑟兰）
      • 裁剪步骤
      • 交点计算公式

在这里插入图片描述

学习目标

  • 了解齐次坐标的概念。
  • 熟练掌握二维基本几何变换矩阵。
  • 熟练掌握Cohen-Sutherland直线段裁剪算法。
  • 掌握中点分割直线段裁剪算法。
  • 掌握Liang-Barsky直线段裁剪算法。
  • 了解Sutherland-Hodgman多边形裁剪算法。

前驱知识

图形几何变换是对图形进行平移变换、比例变换、旋转变换、反射变换和错切变换。

图形几何变换可以分为二维图形几何变换和三维图形几何变换（暂时两种），而二维图形几何变换是三维图形几何变换的基础 。

规范化齐次坐标

在这里插入图片描述

二维几何变换矩阵

在这里插入图片描述

物体变换与坐标变换

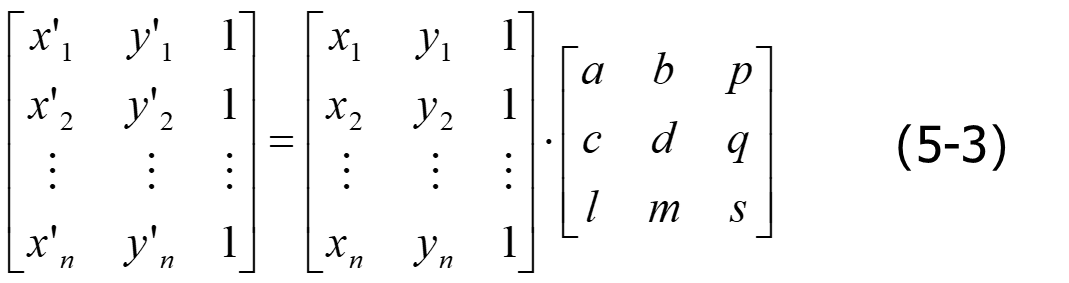
在这里插入图片描述

二维几何变换

在这里插入图片描述
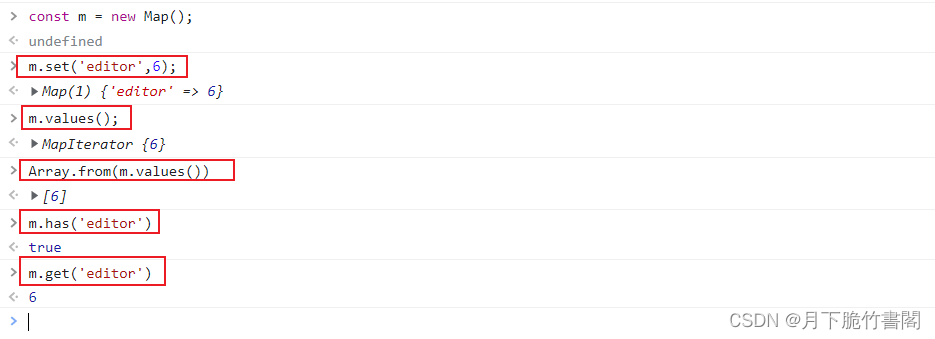
图形顶点集合的规范化齐次坐标矩阵 与 某一变换矩阵 相乘的形式。变换矩阵的定义看式（5-2）

二维图形基本几何变换矩阵

二维图形基本几何变换是指相对于坐标原点和坐标轴进行的几何变换，包括平移（Translate）、比例（Scale）、旋转（Rotate）、反射（Reflect）和错切（shear）5种变换。

物体变换是通过变换物体上每一个顶点实现的，因此以点的二维基本几何变换为例讲解二维图形基本几何变换矩阵 。

平移变换矩阵

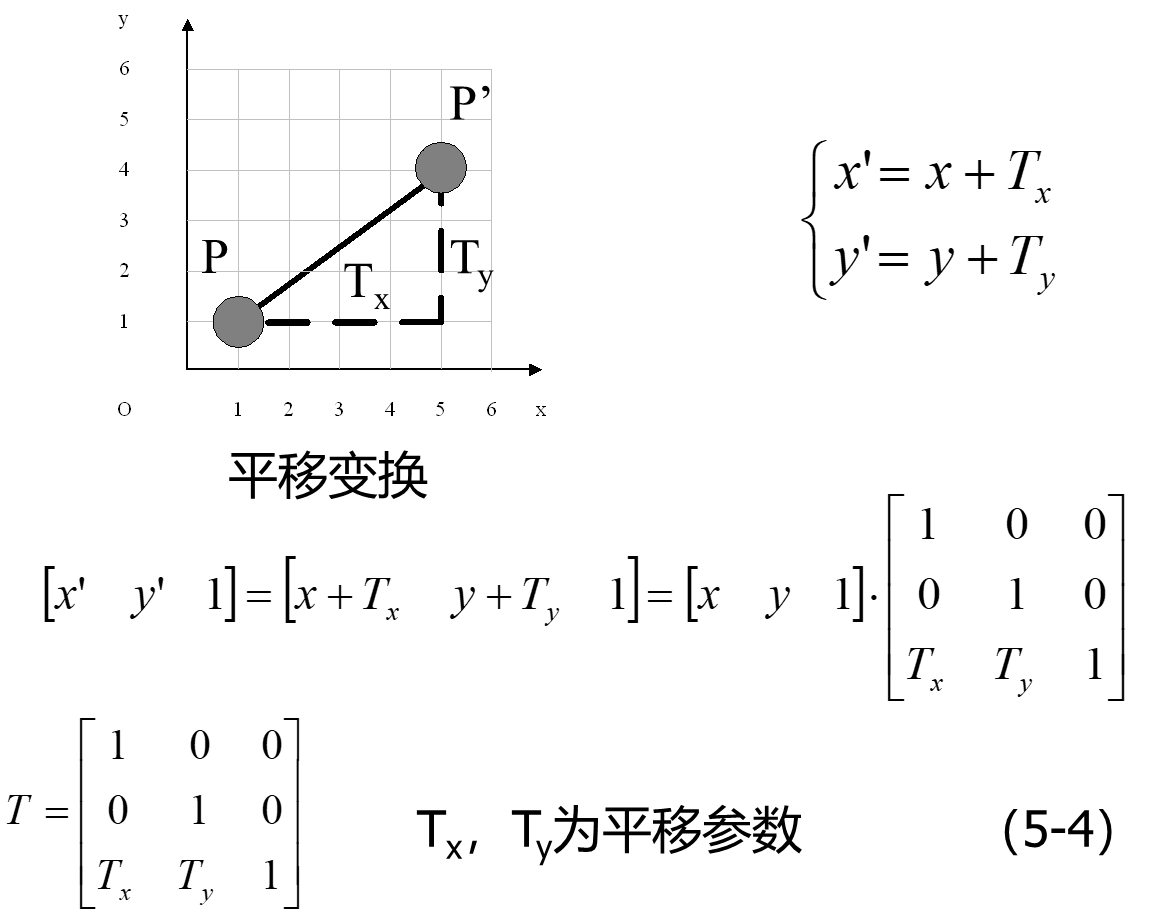
在这里插入图片描述

比例变换矩阵

在这里插入图片描述

旋转变换矩阵

在这里插入图片描述

反射变换矩阵

在这里插入图片描述
在这里插入图片描述

错切变换矩阵

举个例子
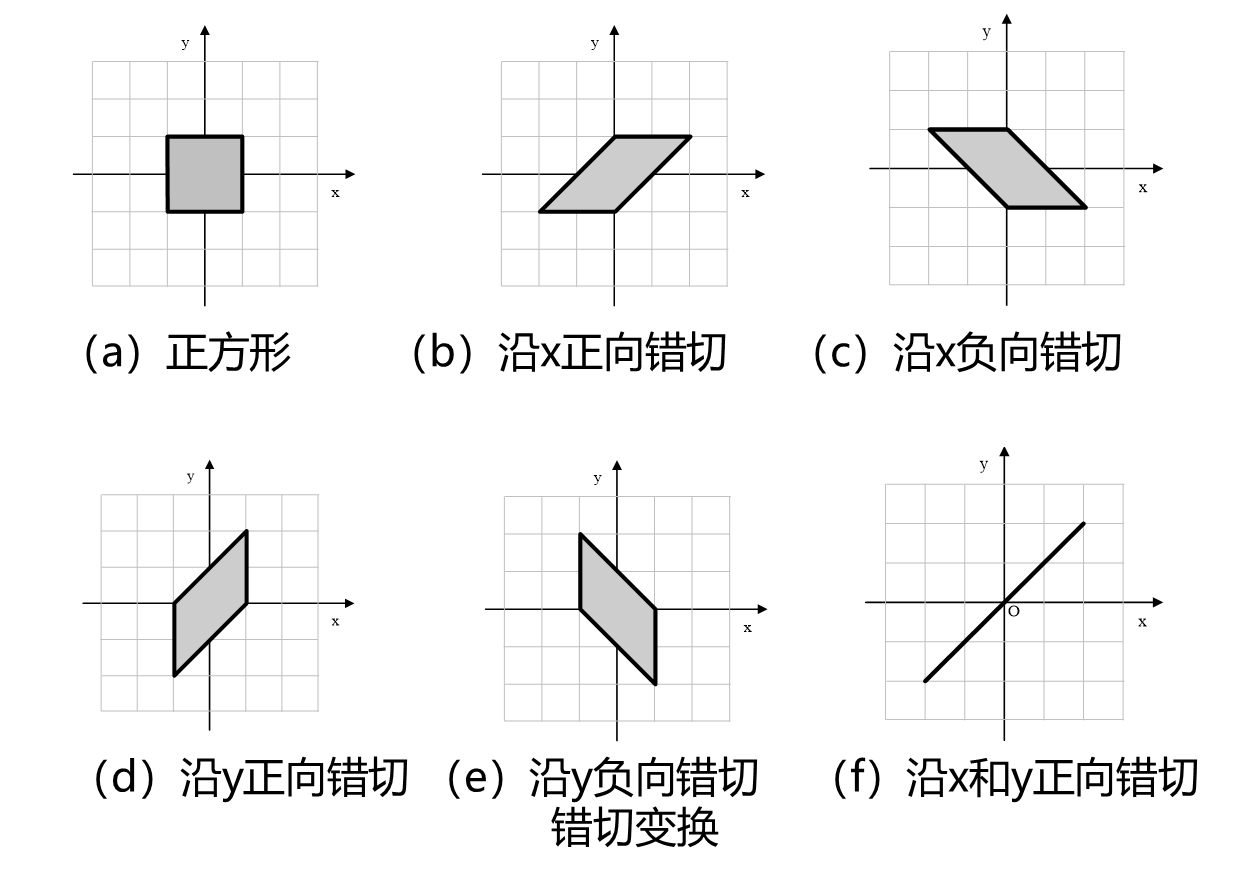
在这里插入图片描述
记住这都是怎么错切的。可以只记变换矩阵。

在这里插入图片描述
一些规律：
在这里插入图片描述

上面讨论的五种变换给出的都是点变换的公式，对于线框模型，图形的变换实际上都可以通过点变换来完成。

例如直线段的变换可以通过对两个顶点坐标进行变换，连接新顶点得到变换后的新直线段；多边形的变换可以通过对每个顶点进行变换，连接新顶点得到变换后的新多边形。曲线的变换可通过变换控制多边形的控制点后，重新绘制曲线来实现。

二维仿射变换

符合下面形式的坐标变换称为二维仿射变换（Affine Transformation）。
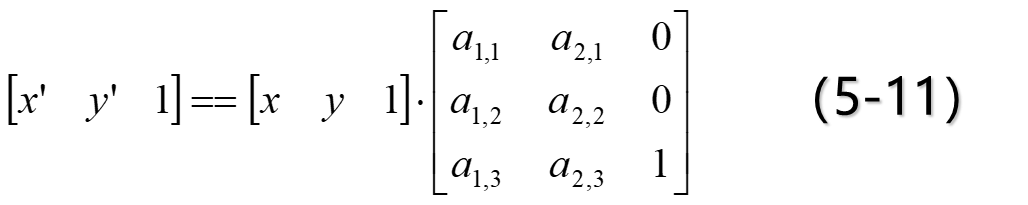
在这里插入图片描述
仿射变换具有平行线变换成平行线，有限点映射到有限点的一般特性。

平移、比例、旋转、反射和错切五种变换都是二维仿射变换的特例，任何一组二维仿射变换总可表示为这5种变换的组合。

二维复合变换

原理：
在这里插入图片描述
相对于任一参考点的比例变换和旋转变换应表达为复合变换形式，

变换方法为（两步）

  • 首先将参考点平移到坐标原点，对坐标原点进行比例变换和旋转变换，
  • 然后再进行反平移将参考点平移回原位置。

在这里插入图片描述
上面右边的图是先把Q和P点们移动到坐标原点。

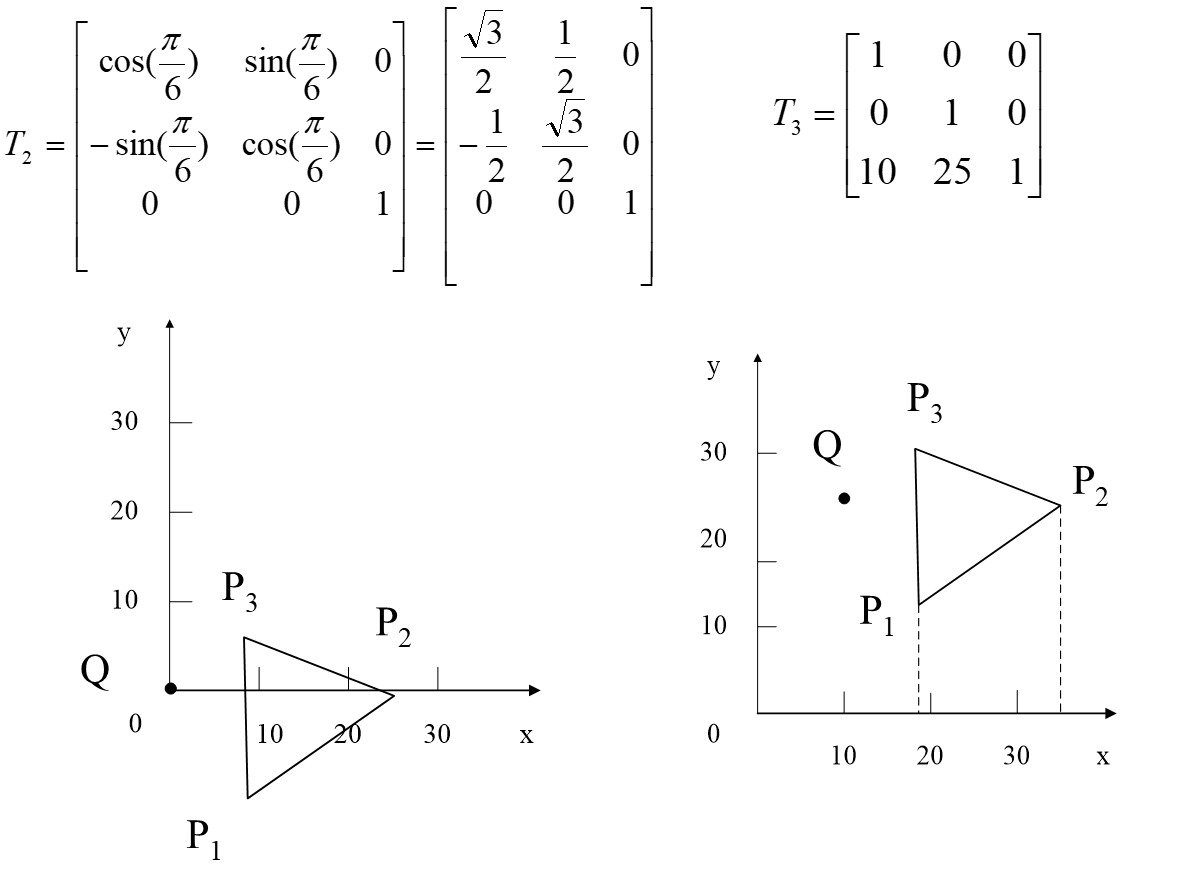
在这里插入图片描述

在这里插入图片描述

相对于任意方向的二维几何变换

相对于任意方向的变换方法是

  • 首先对“任意方向”做旋转变换，使变换方向与坐标轴重合，
  • 然后对坐标轴进行二维基本几何变换，
  • 最后做反向旋转变换，将任意方向还原到原来的方向。

例5-2 将图示三角形相对于轴线y=kx+b作反射变换，计算每一步的变换矩阵。

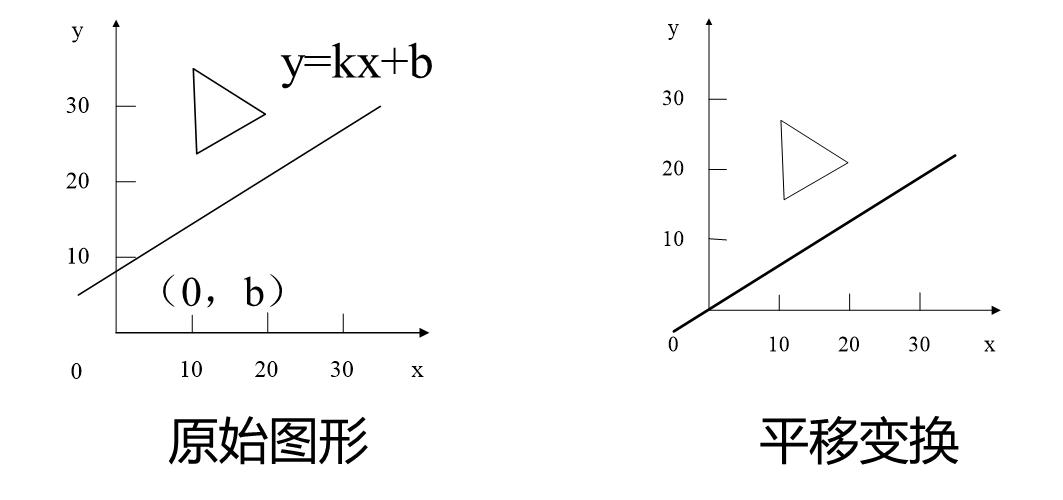
在这里插入图片描述

在这里插入图片描述

首先对“任意方向”做旋转变换，使变换方向与坐标轴重合。↑

然后对坐标轴进行二维基本几何变换↓
在这里插入图片描述

最后做反向旋转变换，将任意方向还原到原来的方向。↓
在这里插入图片描述
代码：

class CTransform//二维几何变换  
{
public:
	CTransform();
	virtual ~CTransform();
	void SetMat(CP2 *,int);
	void Identity();
	void Translate(double,double);//平移变换矩阵
	void Scale(double,double);//比例变换矩阵
	void Scale(double,double,CP2);//相对于任意点的比例变换矩阵
	void Rotate(double);//旋转变换矩阵
	void Rotate(double,CP2);//相对于任意点的旋转变换矩阵
	void ReflectO();//原点反射变换矩阵
	void ReflectX();//X轴反射变换矩阵
	void ReflectY();//Y轴反射变换矩阵
	void Shear(double,double);//错切变换矩阵
	void MultiMatrix();//矩阵相乘
public:
	double T[3][3];
	CP2 *POld;
	int num;
};

void CTransform::Identity()//单位矩阵
{
	T[0][0]=1.0;T[0][1]=0.0;T[0][2]=0.0;
	T[1][0]=0.0;T[1][1]=1.0;T[1][2]=0.0;
	T[2][0]=0.0;T[2][1]=0.0;T[2][2]=1.0;
}
void CTransform::Translate(double tx,double ty)//平移变换矩阵
{
	Identity();
	T[2][0]=tx; 
	T[2][1]=ty; 
	MultiMatrix();	
}
void CTransform::Scale(double sx,double sy)//比例变换矩阵
{
	Identity();
	T[0][0]=sx; 
	T[1][1]=sy; 
	MultiMatrix();	
}

void CTransform::Rotate(double beta)//旋转变换矩阵
{
	Identity();
	double rad=beta*PI/180;
	T[0][0]=cos(rad); T[0][1]=sin(rad);
	T[1][0]=-sin(rad);T[1][1]=cos(rad);
	MultiMatrix();	
}
void CTransform::Rotate(double beta,CP2 p)//相对于任意点的旋转变换矩阵
{
	Translate(-p.x,-p.y);
	Rotate(beta);
	Translate(p.x,p.y);	
}
void CTransform::ReflectO()//原点反射变换矩阵
{
	Identity();
	T[0][0]=-1;
	T[1][1]=-1;
	MultiMatrix();	
}

void CTransform::ReflectX()//X轴反射变换矩阵
{
	Identity();
	T[0][0]=1;
	T[1][1]=-1;
	MultiMatrix();	
}
void CTransform::ReflectY()//Y轴反射变换矩阵
{
	Identity();
	T[0][0]=-1;
	T[1][1]=1;
	MultiMatrix();	
}
void CTransform::Shear(double b,double c)//错切变换矩阵
{
	Identity();
	T[0][1]=b;
	T[1][0]=c;
	MultiMatrix();	
}

void CTransform::MultiMatrix()//矩阵相乘
{
	CP2 *PNew=new CP2[num];	
	for(int i=0;i<num;i++)
	{
		PNew[i]=POld[i];
	}
	for(int j=0;j<num;j++)
	{
		POld[j].x=PNew[j].x*T[0][0]+PNew[j].y*T[1][0]
                                      +PNew[j].w*T[2][0];
		POld[j].y=PNew[j].x*T[0][1]+PNew[j].y*T[1][1]
                                      +PNew[j].w*T[2][1];
		POld[j].w=PNew[j].x*T[0][2]+PNew[j].y*T[1][2]
                                      +PNew[j].w*T[2][2];
	}
	delete []PNew;
}

二维图形裁剪

世界坐标系

描述现实世界中场景的固定坐标系称为世界坐标系，
世界坐标系是实数域坐标系，
根据应用的需要可以选择直角坐标系、圆柱坐标系、球坐标系以及极坐标系等。
在这里插入图片描述

2.用户坐标系

描述物体数学模型的坐标系称为用户坐标系，有时也称为局部坐标系。

用户坐标系也是实数域坐标系。

用户坐标系是可移动坐标系，用户坐标系的原点可以放在物体的任意位置上，坐标系也可以旋转任意角度。

对于立方体，可以将用户坐标系原点放置在立方体中心；对于圆柱，可以将用户坐标系的y轴作为旋转轴。

观察坐标系

观察坐标系是在世界坐标系中定义的坐标系，观察坐标系原点位于视点，z轴垂直于屏幕，正向为视线方向。

二维观察坐标系主要用于指定图形的输出范围。
三维观察坐标系是左手系，用于生成物体的旋转动画。
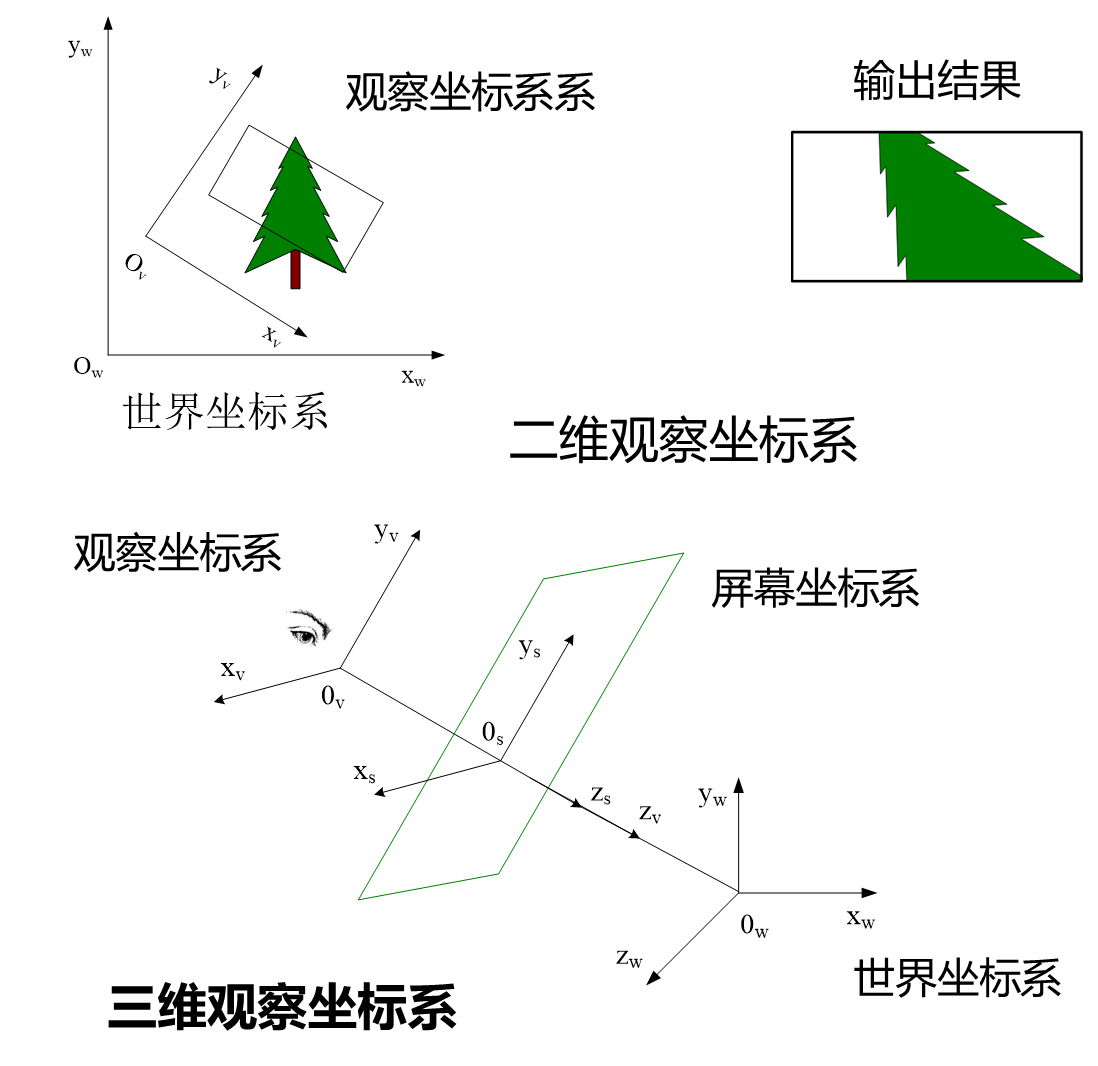
在这里插入图片描述

屏幕坐标系

屏幕坐标系为实数域二维直角坐标系。原点位于屏幕中心，x轴水平向右为正，y轴垂直向上为正。

设备坐标系

显示器等图形输出设备自身都带有一个二维直角坐标系称为设备坐标系。设备坐标系是整数域二维坐标系，原点位于屏幕左上角，x轴水平向右，y轴垂直向下，基本单位为像素。格化到〔0.0，0.0〕到〔1.0，1.0〕的范围内的设备坐标系称为规格化设备坐标系。

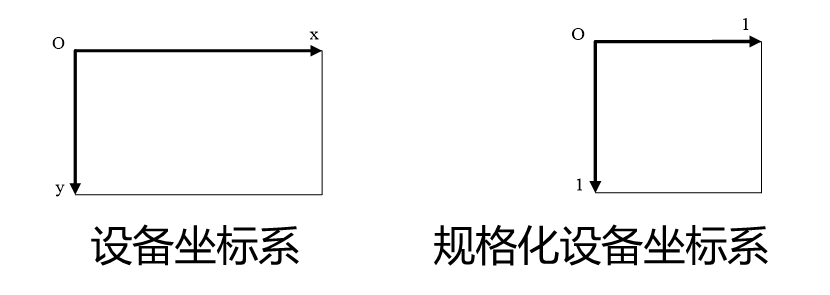
在这里插入图片描述

  1. 规格化设备坐标系独立于具体输出设备。一旦图形变换到规格化设备坐标系中，只要作一个简单的乘法运算即可映射到具体的设备坐标系中。
  2. 由于规格化设备坐标系能统一用户各种图形的显示范围，故把用户图形变换成规格化设备坐标系中的统一大小标准图形的过程叫作图形的逻辑输出。
  3. 把规格化设备坐标系中的标准图形送到显示设备上输出的过程叫作图形的物理输出。

有了规格化设备坐标系后，图形的输出可以在抽象的显示设备上进行讨论，因而这种图形学又称为与设备无关的图形学。

窗口与视区

在观察坐标系中定义的确定显示内容的矩形区域称为窗口。
在屏幕坐标系中定义的输出图形的矩形区域称为视区。

图形输出需要进行从窗口到视区的变换，
只有窗口内的图形才能在视区中输出，
并且输出的形状要根据视区的大小进行调整，这称为窗视变换（Window Viewport Transformation，WVT）。

窗口概念已广泛用于图形系统中，泛指任何可以移动，改变大小、激活或变为无效的屏幕上的矩形区域。

在计算机图形学术语中，窗口回归到其的原始定义，是在观察坐标系中确定输出图形范围的矩形区域。

窗视变换矩阵

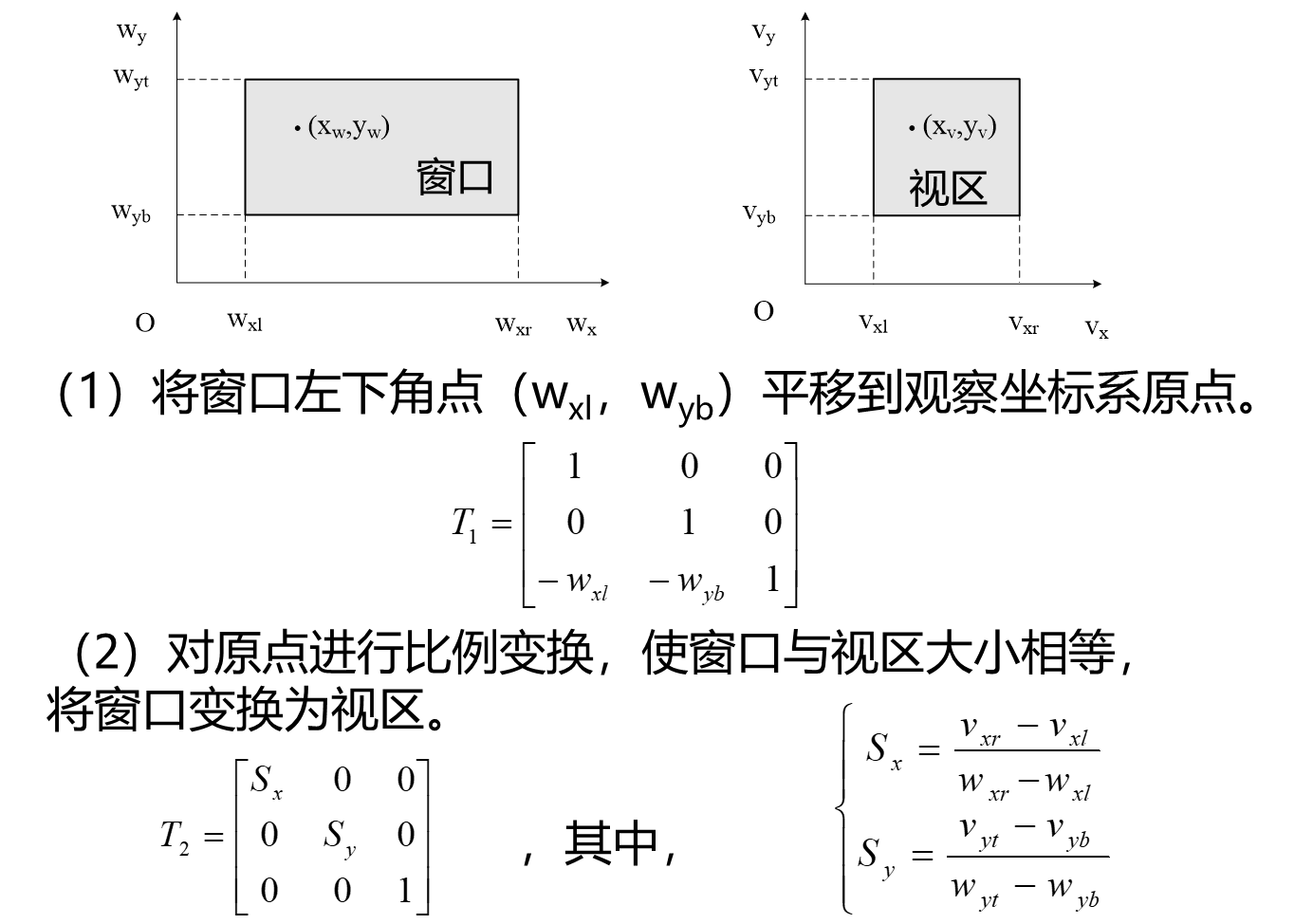
在这里插入图片描述
用到了上面变换矩阵的知识。

在这里插入图片描述

在这里插入图片描述

裁剪算法

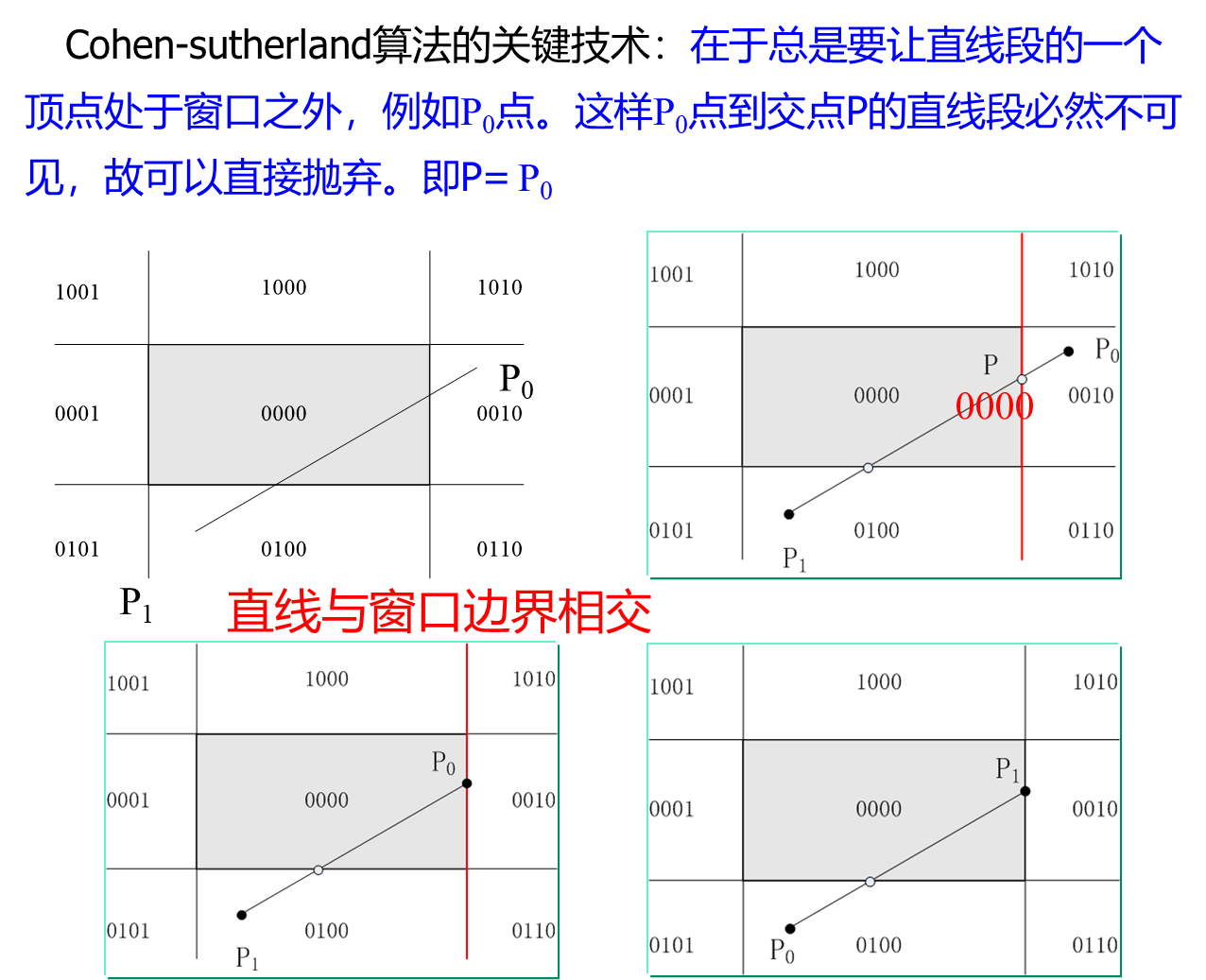
Cohen-Sutherland直线裁剪算法（科恩-萨瑟兰）

最早流行的编码算法。

在二维观察中，需要在观察坐标系下根据窗口大小对二维图形进行裁剪（clipping），只将位于窗口内的图形变换到视区输出。

直线段裁剪是二维图形裁剪的基础，裁剪的实质是判断直线段是否与窗口相交，如相交则进一步确定直线段上位于窗口内的部分。

每段直线的端点都被赋予一组四位二进制代码，称为区域编码(region code，RC)，用来标识直线段端点相对于窗口边界及其延长线的位置。

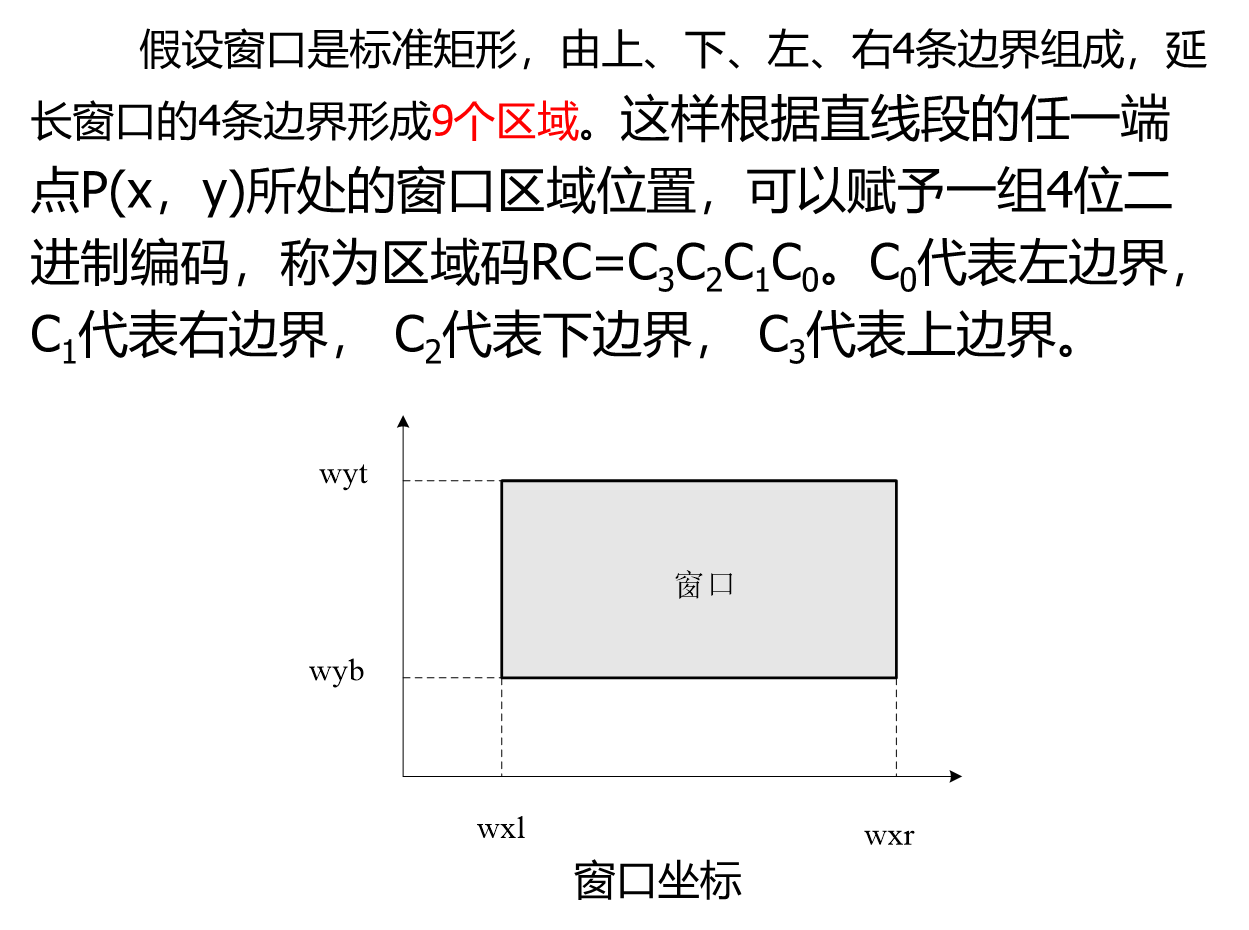
在这里插入图片描述
在这里插入图片描述
为了保证 窗口内 及 窗口边界上 直线段端点 的 编码 为 零，定义规则如下：

在这里插入图片描述

这个不好记啊，尤其是学了那么多东西之后。

裁剪步骤

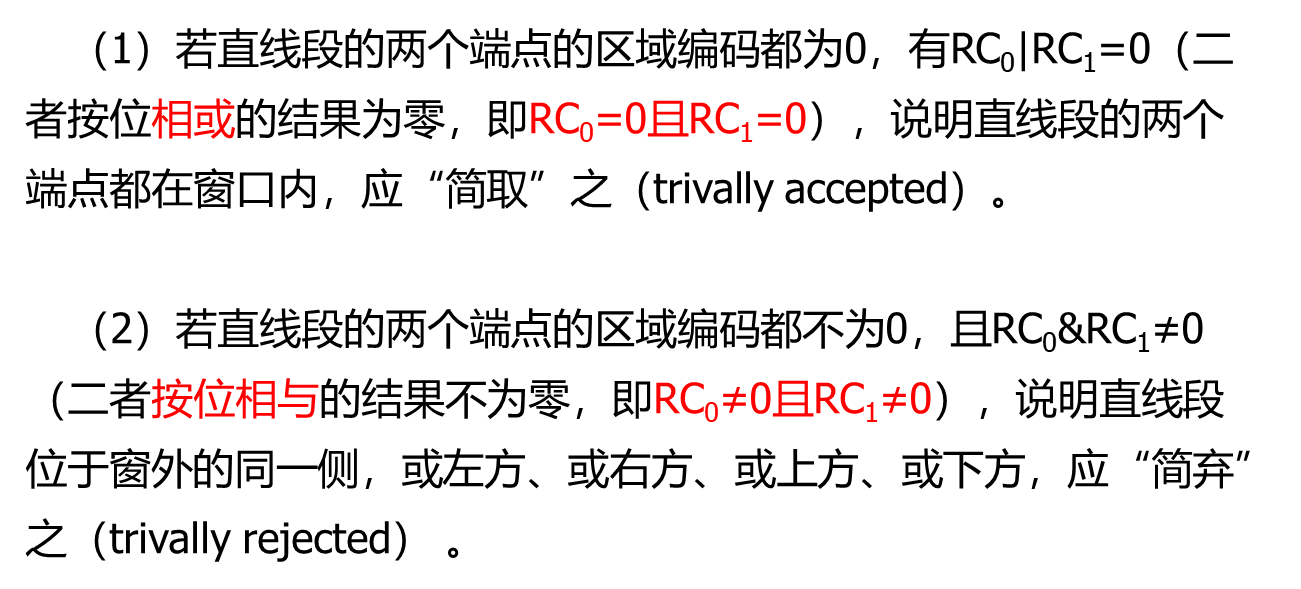
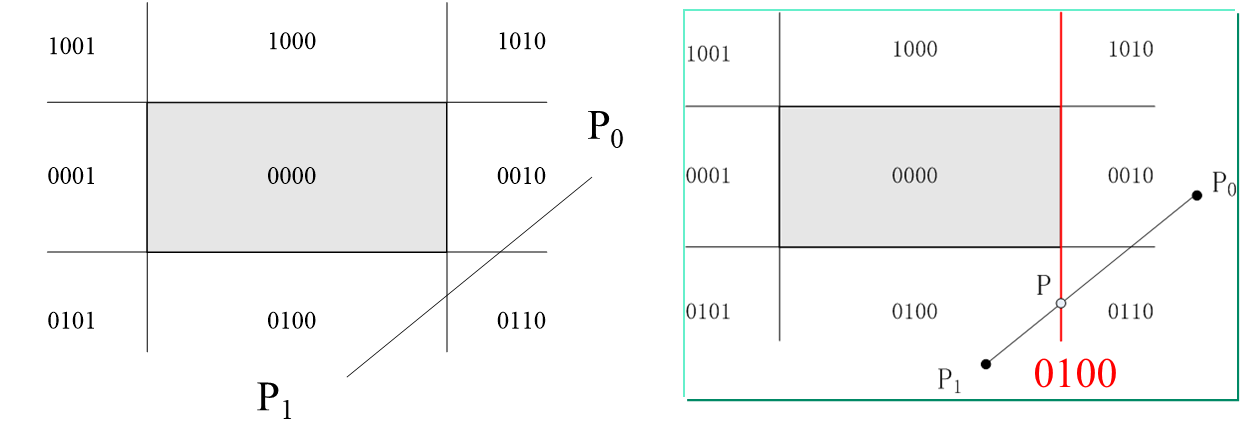
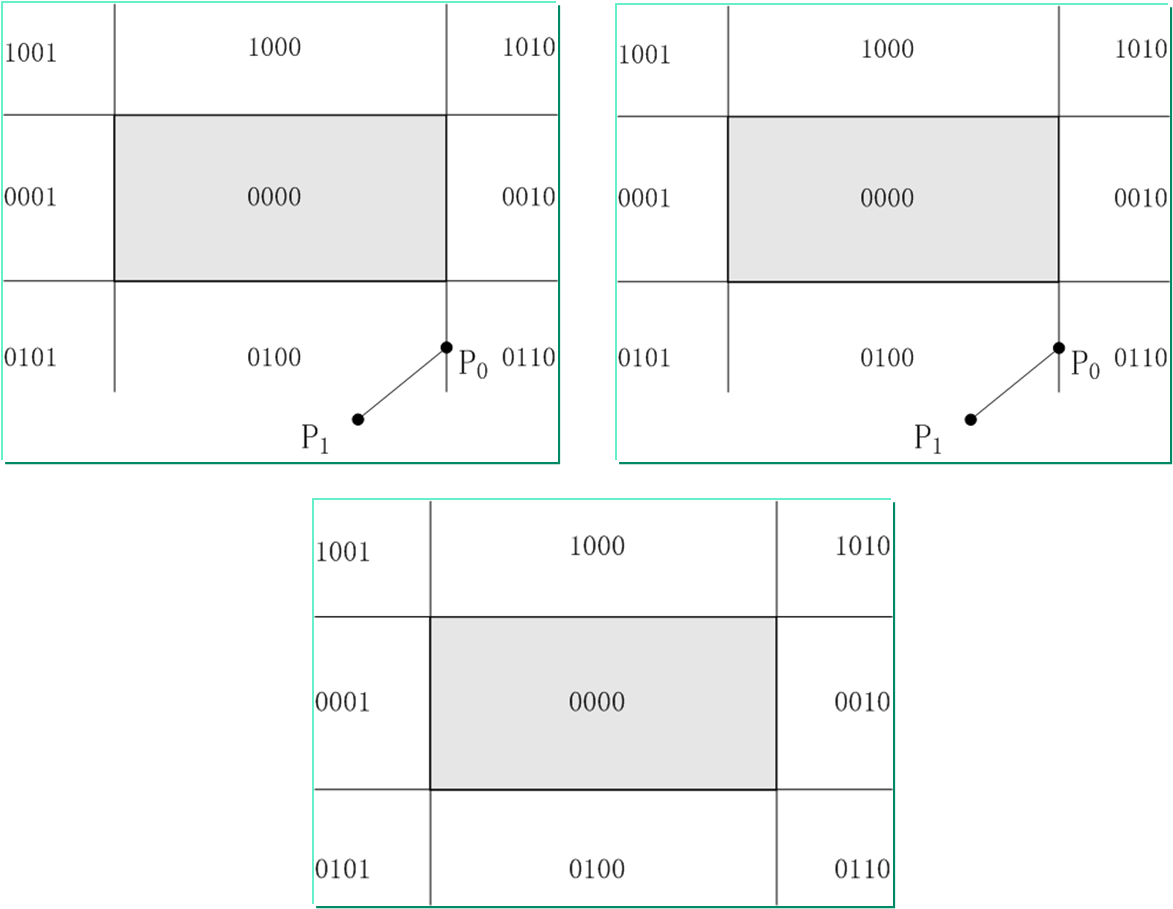
在这里插入图片描述
（3）若直线段既不满足“简取”也不满足“简弃”的条件，则需要与窗口进行“求交”判断。这时，直线段必然与窗口边界或窗口边界的延长线相交，分两种情况处理。
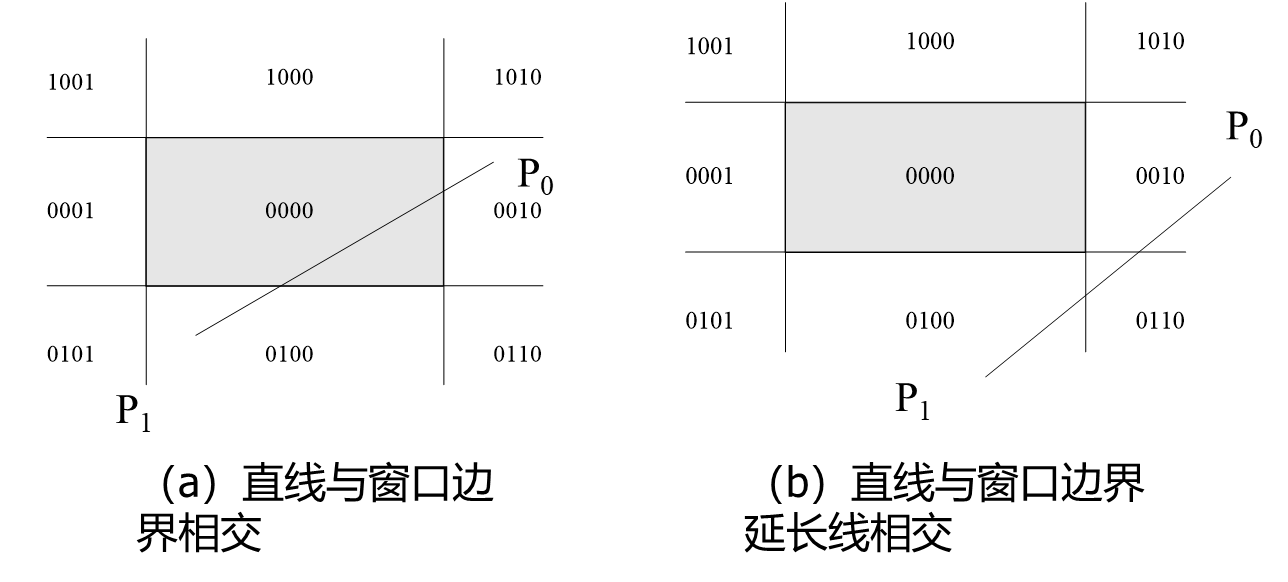
在这里插入图片描述

直线与窗口边界相交的情况

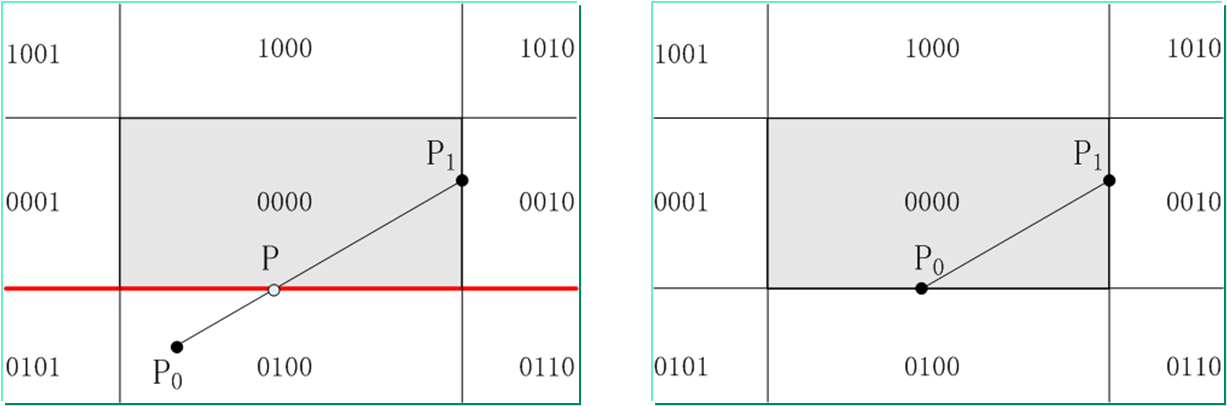
在这里插入图片描述

在这里插入图片描述

直线与窗口边界延长线相交的情况
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

交点计算公式

在这里插入图片描述
代码

#define LEFT        1    //代表:0001
#define RIGHT      2    //代表:0010
#define BOTTOM   4   //代表:0100
#define TOP          8   //代表:1000
void CTestView::EnCode(CP2 &pt)//编码函数
{
	pt.rc=0;
	if(pt.x<Wxl)
	     pt.rc=pt.rc | LEFT;
	else if(pt.x>Wxr)
	     pt.rc=pt.rc | RIGHT;
	if(pt.y<Wyb)
	     pt.rc=pt.rc | BOTTOM;
	else if(pt.y>Wyt)
	     pt.rc=pt.rc | TOP;	
}

#define LEFT        0x1    //代表:0001
#define RIGHT      0x2    //代表:0010
#define BOTTOM   0x4   //代表:0100
#define TOP          0x8   //代表:1000

int  EnCode(double x , double y , int Wxl , int Wxr , int wyb , int wyt)
{
	rc = 0;
	if(x < Wxl)     rc = rc | LEFT;
	if(x > Wxr)     rc = rc | RIGHT;
	if(y < Wyb)    rc = rc | BOTTOM;
	if(y > Wyt)     rc = rc | TOP;
         return rc	;
}

void CTestView::Cohen()//Cohen-Sutherland算法
{
	CP2 p;//交点坐标
	EnCode(P[0]);//起点编码
	EnCode(P[1]);//终点编码
	while(P[0].rc!=0 || P[1].rc!=0)//处理至少一个顶点在窗口外
	{
		if((P[0].rc & P[1].rc)!=0)//简弃之
		{
			PtCount=0;
			return;
		}
		if(0==P[0].rc)//确保P[0]位于窗口之外
		{
			CP2 Temp;
			Temp=P[0];
			P[0]=P[1];
			P[1]=Temp;
		}
                       UINT RC=P[0].rc;
		double k=(P[1].y-P[0].y)/(P[1].x-P[0].x);//斜率
		
if(RC & LEFT)//P[0]点位于窗口的左侧
		{
			p.x=Wxl;//计算交点y坐标
			p.y=k*(p.x-P[0].x)+P[0].y;
		}
		else if(RC & RIGHT)//P[0]点位于窗口的右侧
		{
			p.x=Wxr;//计算交点y坐标
			p.y=k*(p.x-P[0].x)+P[0].y;
		}
		else if(RC & BOTTOM)//P[0]点位于窗口的下侧
		{
			p.y=Wyb;//计算交点x坐标
			p.x=(p.y-P[0].y)/k+P[0].x;
		}			
		else if(RC & TOP)//P[0]点位于窗口的上侧
		{
			p.y=Wyt;//计算交点x坐标
			p.x=(p.y-P[0].y)/k+P[0].x;
		}
        EnCode(p);
		P[0]=p;
         ｝
｝

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/186299.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

VSCode中设置Python语言自动格式化的方案

VSCode中设置Python语言自动格式化的方案

安装Python扩展 在VSCode的扩展&#xff08;Externsions&#xff09;中使用下面命令检索Python扩展 category:debuggers Python 打开一个Python文件&#xff0c;可以在VSCode的右下角看到运行环境。 安装PEP8 python3.10 -m pip install -U autopep8 安装Flake8 python3.10 …
阅读更多...
上百个数字经济新场景 低代码完美搭建 实现项目落地

上百个数字经济新场景 低代码完美搭建 实现项目落地

数字经济 自人类社会进入信息时代以来&#xff0c;数字技术的快速发展和广泛应用衍生出数字经济(Digital Economy)。与农耕时代的农业经济&#xff0c;以及工业时代的工业经济大有不同&#xff0c;数字经济是一种新的经济、新的动能&#xff0c;新的业态&#xff0c;其引发了社…
阅读更多...
MicroBlaze系列教程（3）：AXI_TIMER的使用

MicroBlaze系列教程（3）：AXI_TIMER的使用

文章目录 @[toc]AXI_TIMER简介常用函数使用示例参考资料工程下载本文是Xilinx MicroBlaze系列教程的第3篇文章。 AXI_TIMER简介 AXI_TIMER支持两路可编程32位计数器，可以配置为中断、捕获、PWM模式，两个32位计数器可以级联为一个64位计数器。 IP核支持的最高频率： 常用…
阅读更多...
nacos 服务发现获取列表源码分析

nacos 服务发现获取列表源码分析

nacos 服务发现获取列表源码是注册中心最重要的技术点之一&#xff0c;其获取服务列表理论上是在首次接口调用时获取&#xff0c;有时候配置饥饿加载&#xff0c;即服务启动时就获取服务列表&#xff1a;今天我们从一个入口解析获取配置列表; 一、客户端源码 1、自动装配&…
阅读更多...
推荐系统之推荐缓存服务

推荐系统之推荐缓存服务

5.6 推荐缓存服务 学习目标 目标 无应用 无 5.6.1 待推荐结果的redis缓存 目的&#xff1a;对待推荐结果进行二级缓存&#xff0c;多级缓存减少数据库读取压力步骤&#xff1a; 1、获取redis结果&#xff0c;进行判断 如果redis有&#xff0c;读取需要推荐的文章数量放回&am…
阅读更多...
（深度学习快速入门）第四章第一节：基础图像处理知识

（深度学习快速入门）第四章第一节：基础图像处理知识

文章目录一&#xff1a;位图和矢量图二&#xff1a;图像分辨率三&#xff1a;颜色模式&#xff08;1&#xff09;RGB&#xff08;2&#xff09;HSB&#xff08;2&#xff09;灰度图四&#xff1a;通道五&#xff1a;亮度、对比度和饱和度六&#xff1a;图像平滑和锐化&#xff…
阅读更多...
D3股权穿透图

D3股权穿透图

前言&#xff1a;最近做了一个项目&#xff0c;主要就是实现各种类似企查查的各种图谱&#xff0c;欢迎交流。后期将完成的谱图全部链接上&#xff0c;目前已大致实现了&#xff1a; 【企业关系图谱】、【企业构成图谱】、【股权穿透图】、【股权结构图】、【关联方认定图】 准…
阅读更多...
【蓝桥杯基础题】2018年省赛—日志统计

【蓝桥杯基础题】2018年省赛—日志统计

&#x1f451;专栏内容&#xff1a;蓝桥杯刷题⛪个人主页&#xff1a;子夜的星的主页&#x1f495;座右铭&#xff1a;前路未远&#xff0c;步履不停 目录一、题目描述1.问题描述2.输入格式3.输出格式4.一个例子二、题目分析1、暴力法2、双指针三、代码汇总1、暴力代码汇总2、双…
阅读更多...
【Mysql第一期 数据库概述】

【Mysql第一期 数据库概述】

文章目录1. 为什么要使用数据库2. 数据库与数据库管理系统2.1 数据库的相关概念2.2 数据库特点2.3SQL优点3.常见的数据库介绍1.Oracle2.SQL Server3.MySQL4.Access5.DB26.PostgreSQL7.SQLite8.informix4. MySQL介绍4.1Mysql重大历史事件4.2 关于MySQL 8.04.3 Why choose MySQL?…
阅读更多...
linux内核读文件代码分析

linux内核读文件代码分析

linux下“一切皆文件”，所有设备都可以被抽象成文件，用户态可以通过open、read、write、llseek等api操作一个文件，通过系统调用进入内核态，最终访问到pagecache/磁盘上的数据，然后返回给用户态。 kernel version：v6.2-rc4 社区master主干 用户态应用程序调用read接口，通…
阅读更多...
【转载】车载传感器与云端数据交换标准SensorIS的理解与使用

【转载】车载传感器与云端数据交换标准SensorIS的理解与使用

原文 https://zhuanlan.zhihu.com/p/386277784 1、什么是SensorIS?SensorIS全称是Sensor Interface Specification&#xff0c;翻译为中文就是传感器接口规范&#xff0c;是由来自全球汽车行业的主机厂、地图和数据提供商、传感器制造商和电信运营商共同组成的开放团体发布的一…
阅读更多...
JavaEE day10 初识SpringMVC

JavaEE day10 初识SpringMVC

JSON简介 JSON &#xff1a;JavaScript Object Notation JS对象表示法 是轻量级的文本数据交换格式&#xff0c;但是JSON仍然独立于语言和平台。其解析器和库支持许多不同的编程语言。目前非常多的动态编程语言&#xff08;java&#xff0c;PHP&#xff09;都支持JSON。JSON…
阅读更多...
禅道好用吗？优缺点及类似10大项目管理系统介绍

禅道好用吗？优缺点及类似10大项目管理系统介绍

类似禅道的十大项目管理软件&#xff1a;1、一站式研发项目管理软件PingCode&#xff1b;2、通用型项目协作工具Worktile&#xff1b;3、开源项目管理软件Redmine&#xff1b;4、免费项目管理软件Trello&#xff1b;5、无代码项目管理软件Monday&#xff1b;6、IT项目追踪管理工…
阅读更多...
面试宝典-数据库基础

面试宝典-数据库基础

数据库基础前言一、数据库1.1 sql练习题1.2 sql语句执行顺序1.3 sql语句编写前言 本文主要记录B站视频视频链接的内容&#xff0c;做到知识梳理和总结的作用&#xff0c;项目git地址。 一、数据库 1.1 sql练习题 user表数据: idusername1张三2李四3王五4小刘 user_role表数…
阅读更多...
CrackQL：一款功能强大的图形化密码爆破和模糊测试工具

CrackQL：一款功能强大的图形化密码爆破和模糊测试工具

关于CrackQL CrackQL是一款功能强大的图形化密码爆破和模糊测试工具&#xff0c;在该工具的帮助下&#xff0c;广大研究人员可以针对密码安全和应用程序安全进行渗透测试。 除此之外&#xff0c;CrackQL同时也是一款通用的GraphQL渗透测试工具&#xff0c;它可以控制速率限制…
阅读更多...
垃圾分类智能分析系统 yolov7

垃圾分类智能分析系统 yolov7

垃圾分类智能分析系统应用pythonyolov7网络模型深度学习识别技术&#xff0c;自动识别违规投放行为并现场进行语音提示实时预警。如垃圾满溢抓拍预警、人脸识别、工服识别、厨余垃圾混投未破袋识别预警、垃圾落地识别预警、人来扔垃圾语音提醒等。我们选择当下YOLO最新的卷积神…
阅读更多...
数组去重的七种方法

数组去重的七种方法

数组去重的七种方法1. 双重for循环2. forindexOf3.es6 set4.filter5.includes6.创建一个新的object7.new Map()1. 双重for循环 第1种是定义一个新的空数组&#xff0c;再执行嵌套双循环&#xff0c;监测空数组中如果没有的元素&#xff0c;push进空数组中。这个方法考察了conti…
阅读更多...
AcWing - 寒假每日一题2023（DAY 16——DAY 20）

AcWing - 寒假每日一题2023（DAY 16——DAY 20）

文章目录一、AcWing 4455. 出行计划&#xff08;简单&#xff09;1. 实现思路2. 实现代码二、AcWing 4510. 寻宝&#xff01;大冒险&#xff01;&#xff08;简单&#xff09;1. 实现思路2. 实现代码三、AcWing 3422. 左孩子右兄弟&#xff08;中等&#xff09;1. 实现思路2. 实…
阅读更多...
【MySQL】过年没有回老家，在出租屋里整理了一些思维导图

【MySQL】过年没有回老家，在出租屋里整理了一些思维导图

Xmind导图知识点Mysql知识点SQL知识点Mybatis知识点面试题分享MySQL部分Mybatis部分Mysql知识点 通过下面的图片可以看出&#xff0c;MySQL基础语法分为四部分&#xff1a;连接数据库&#xff0c;对数据库的操作&#xff0c;对表中的数据操作&#xff0c;对表操作等等。 SQL…
阅读更多...
python exe程序注册为window系统服务

python exe程序注册为window系统服务

1、使用pyinstaller将py打包成exe 1、安装 pip install pyinstaller2、打包成exe可执行文件 pyinstaller -F packTest.py #packTest.py为待打包的py文件打包成功后会在同级目录中生成两个文件夹和一个文件&#xff0c;分别为dist和build文件夹&#xff0c;以及一份与.py文件同…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023