文章目录
- 一:位图和矢量图
- 二:图像分辨率
- 三:颜色模式
- (1)RGB
- (2)HSB
- (2)灰度图
- 四:通道
- 五:亮度、对比度和饱和度
- 六:图像平滑和锐化
- (1)图像平滑
- (2)图像锐化
- 七:图像边缘提取
- 八:形态学运算
一:位图和矢量图
- 位图:由基本单位像素(pixel)构成,像素可以进行不同的排列和染色以构成图样,放大位图时本质是在增大单个像素,所以会使得图像呈现锯齿状。PhotoShop是一款图像处理软件
- 矢量图:是用一系列计算指令来表示的图,本质是多个数学表达式,矢量图只能靠软件生成,放大不会模糊,因为它和分辨率没有关系。Adobe Illustraotr是一款矢量绘图软件

二:图像分辨率
图像分辨率:是指每英寸图像内的的像素点数,单位为ppi。分辨率越大图像就会越清晰,当然文件也会越大

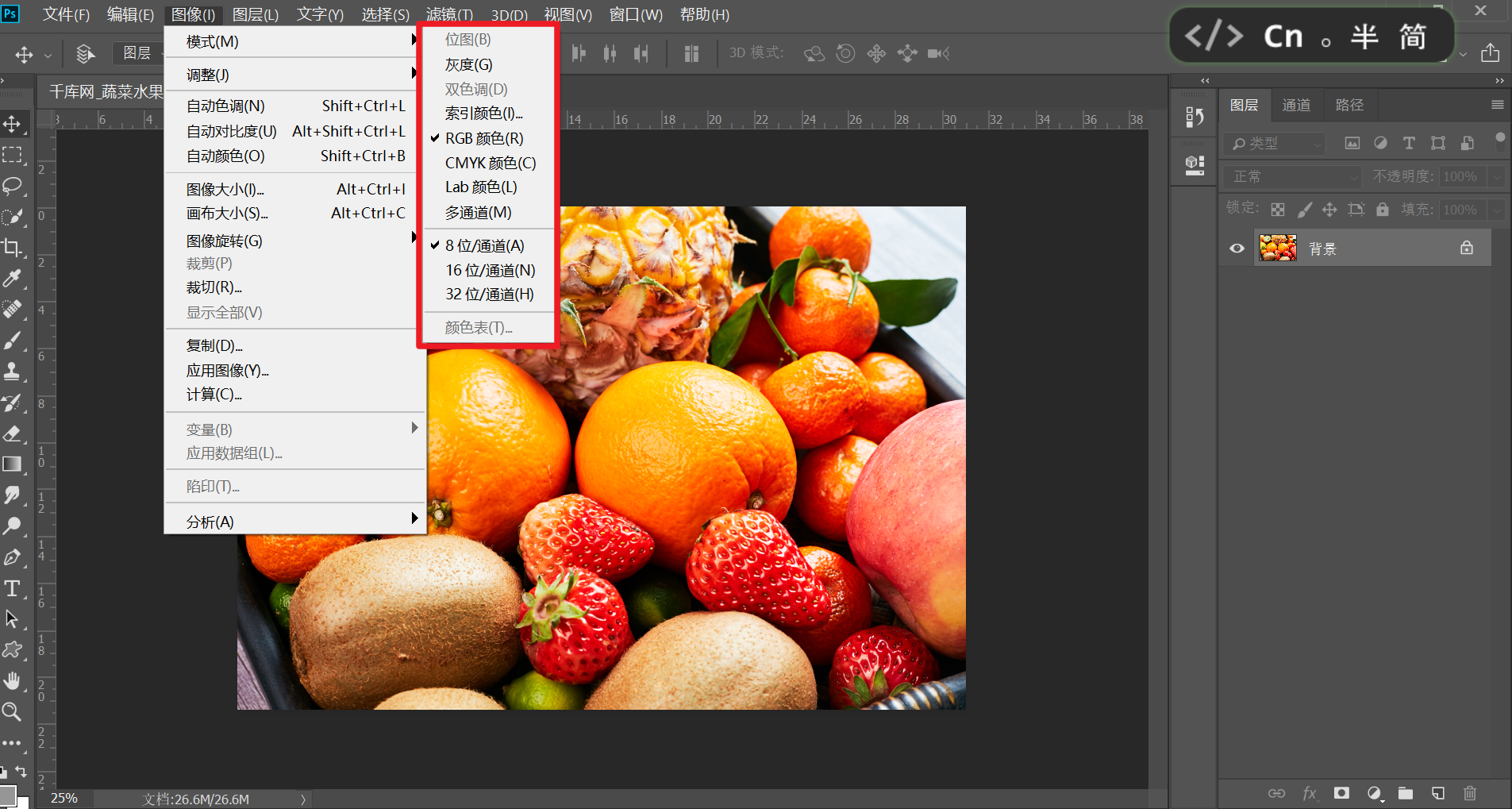
三:颜色模式
颜色模式:每一种颜色在计算机中都对应一种颜色编码,编码方式不同,会形成各种各样的颜色模式,主要有
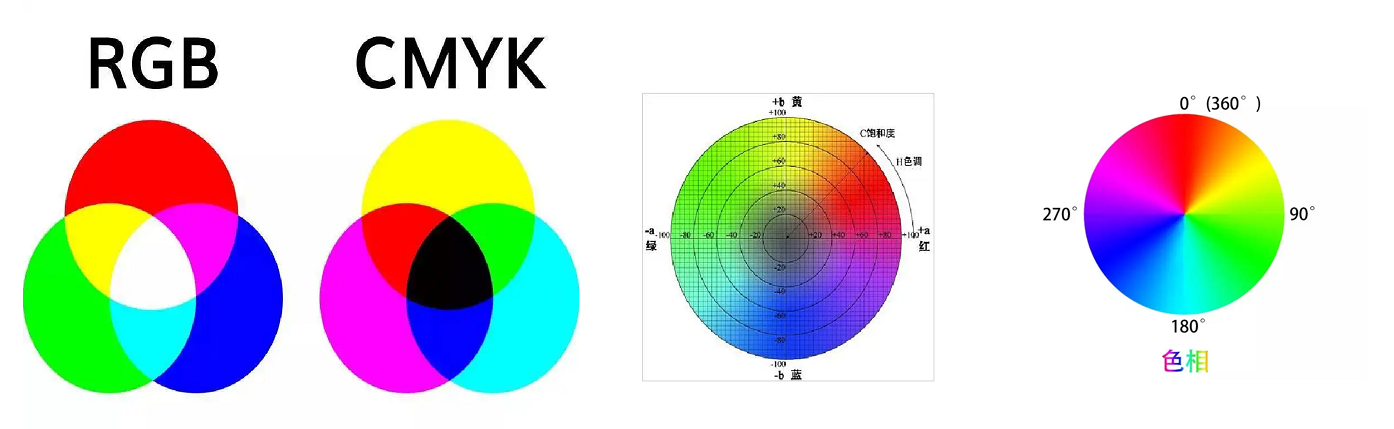
- RGB(重点): 分别表示红色®、绿色(G)、蓝(B),屏幕显示时最佳模式,属于加色模式(颜色越多越亮)
- CMYK: C代表青色,M代表洋红色,Y代表黄色,K代表黑色,RGB不适合打印,所以CMYK主要用于印刷,属于减色模式(颜色越少越暗)
- lab: Lab模式弥补了RGB和CMYK两种色彩模式的不足。Lab模式由三个通道组成,但不是R、G、B通道。它的一个通道是亮度,即L。另外两个是色彩通道,用A和B来表示。A通道包括的颜色是从深绿色(底亮度值)到灰色(中亮度值)再到亮粉红色(高亮度值);B通道则是从亮蓝色(底亮度值)到灰色(中亮度值)再到黄色(高亮度值)。因此,这种色彩混合后将产生明亮的色彩
- HSB: H表示色相,S表示饱和度,B表示亮度
- 灰度图:
(1)RGB
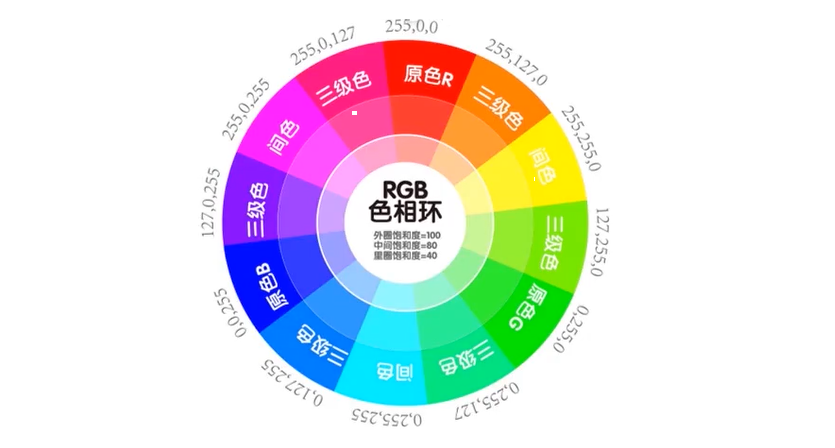
RGB:为光的三原色,分别表示红色®、绿色(G)、蓝(B),三种色彩叠加形成了其它的色彩
- 每种颜色都有256个亮度水平级,所以三种色彩叠加就形成1670万种颜色了
- 所有显示器、投影设备以及电视机等等许多设备都依赖于这种加色模式来实现
- RGB模式并不适合于打印,因为RGB模式所提供的有些色彩已经超出了打印的范围之外,因此在打印一幅真彩色的图象时,就必然会损失一部分亮度,并且比较鲜艳的色彩肯定会失真的
(2)HSB
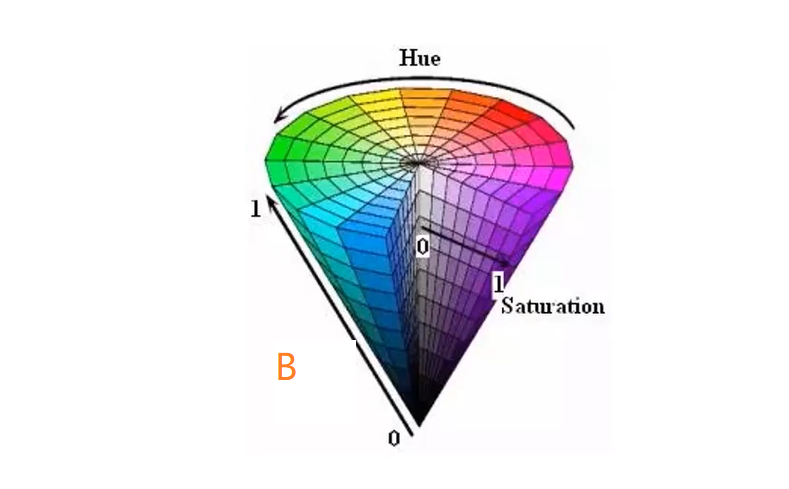
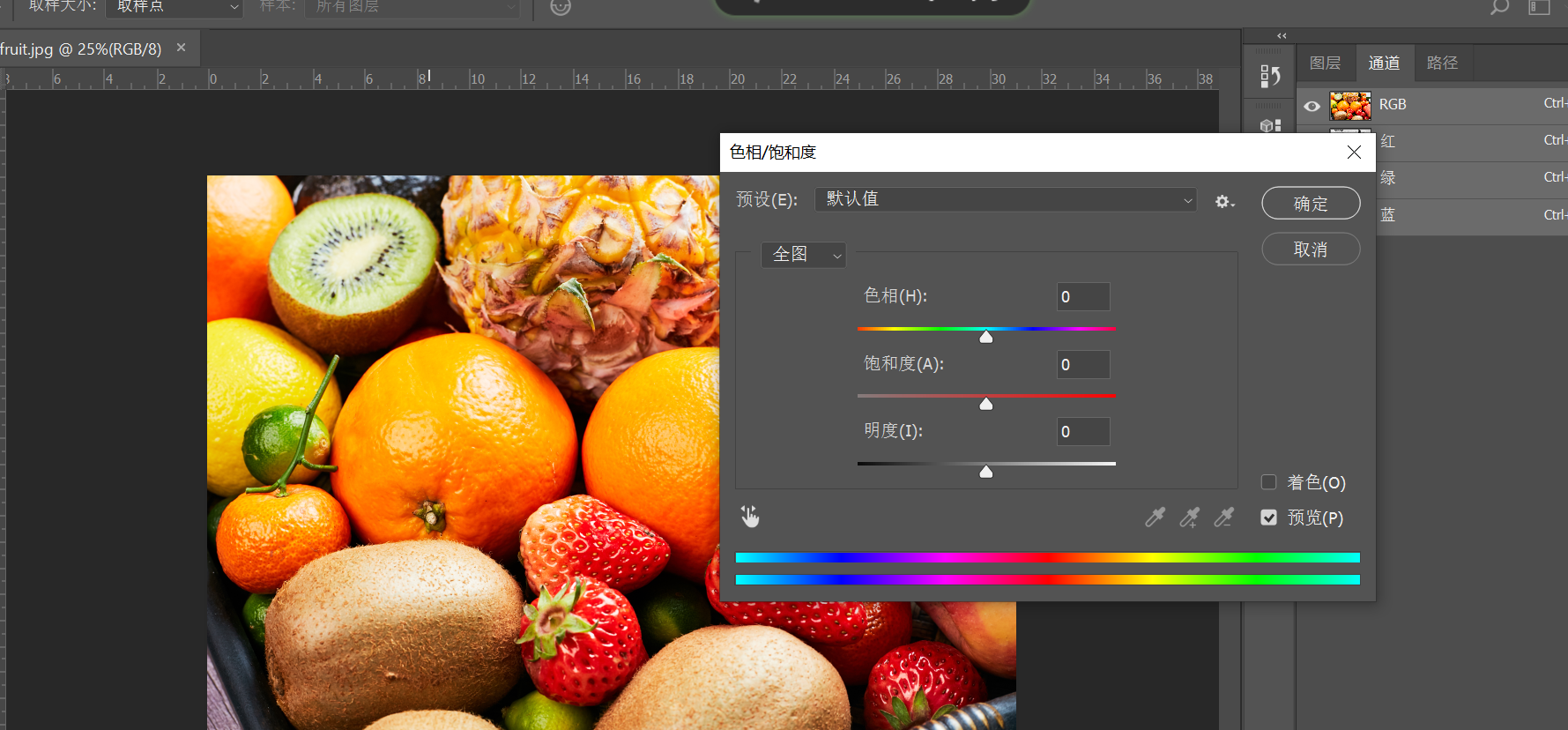
HSB:H表示色相,S表示饱和度,B表示亮度
- 色相:是纯色,即组成可见光谱的单色。红色在0度,绿色在120度,蓝色在240度。它基本上是RGB模式全色度的饼状图
- 饱和度:表示色彩的纯度,为0时为会色。白、黑和其他灰色色彩都没有饱和度的。在最大饱和度时,每一色相具有最纯的色光
- 亮度:是色彩的明亮度
(2)灰度图
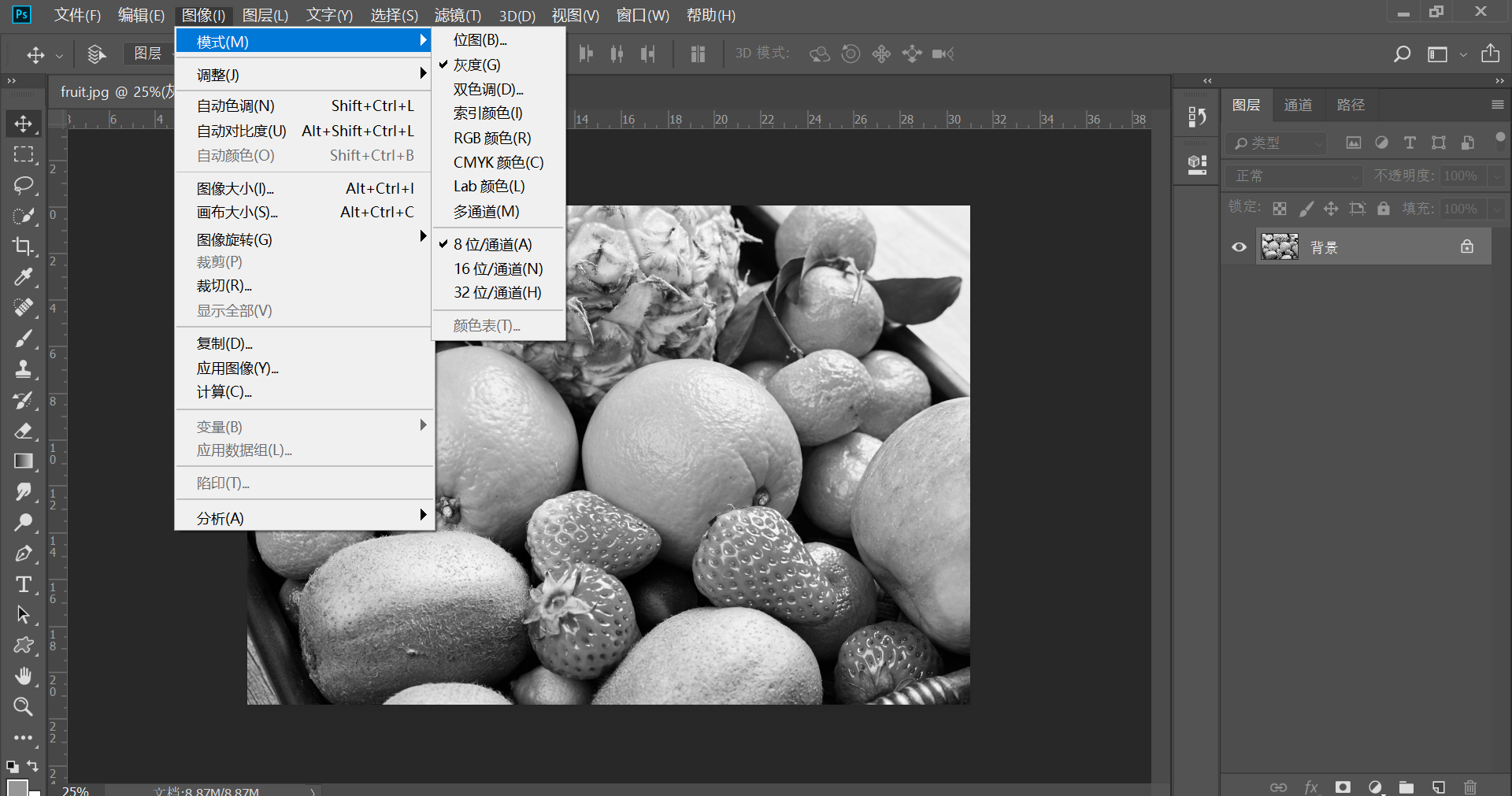
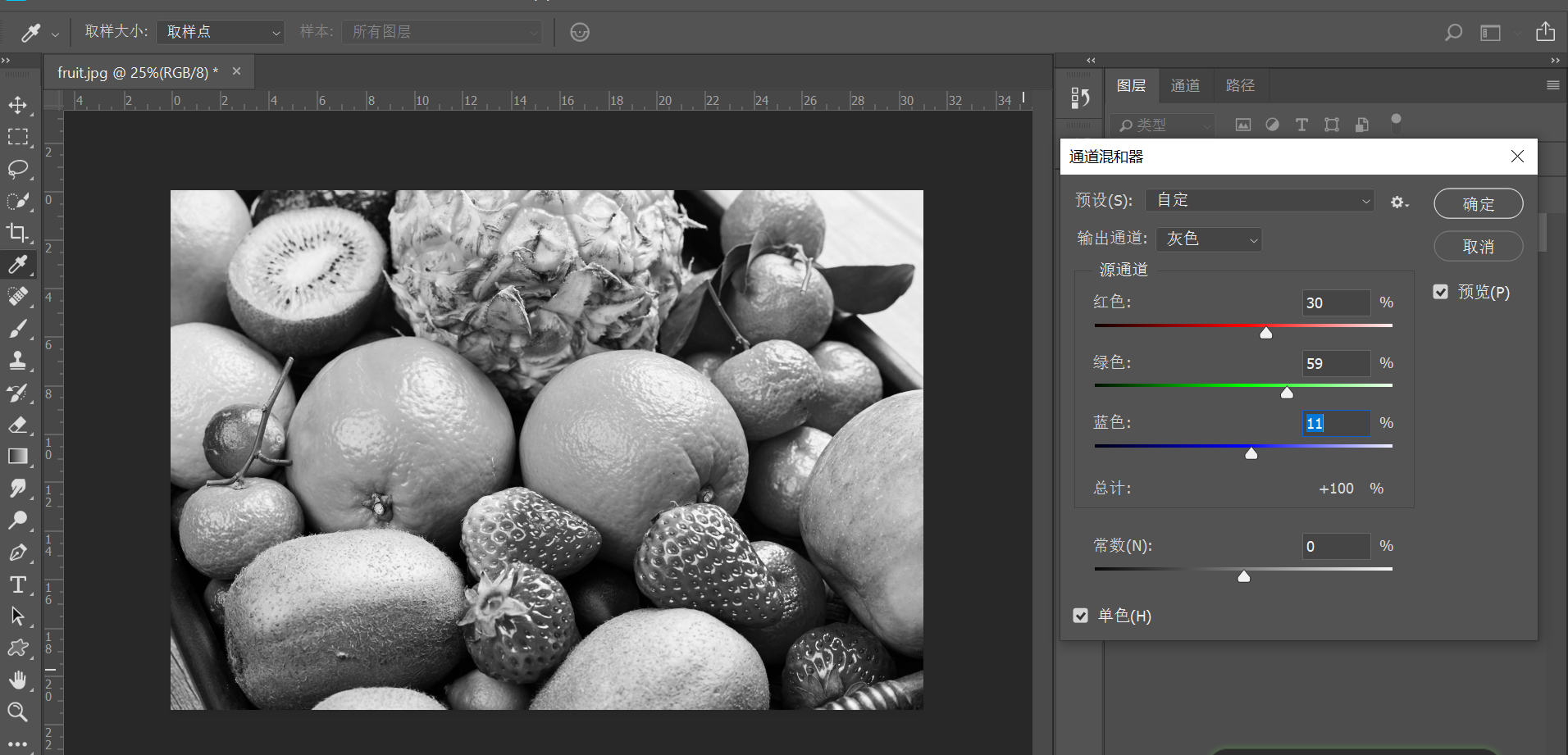
灰度图:当需要关注图像纹理信息而不需要关注颜色信息时,可以使用灰度图。灰度图实际上就是把C变成了1,形成了一个H×W的矩阵,使用0代表黑色,1、255或65635代表白色,将一张RGB图像转为灰度图像时有如下方法
- 心理学公式:R×0.299 + G×0.587 + B×0.114
- 平均值:(R+G+B) / 3
- 取任意:Gray = G (取绿色通道)
例如,使用OpenCV操作
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
# 读入图像
image = cv.imread('./image/fruit.jpg')
# OpenCV是按照B G R读入的,所以这里转为R G B
RGB = cv.cvtColor(image, cv.COLOR_BGR2RGB)
print("H×W×C:", RGB.shape)
print(RGB.dtype)
# 将三个通道分开
(R, G, B) = cv.split(RGB)
# 乘以相应比例
R = R * 0.299
G = G * 0.587
B = B * 0.114
# 重新组装
new_RGB = np.zeros((RGB.shape[0], RGB.shape[1])) # 注意类型为float64
new_RGB = (R + G + B)
new_RGB = new_RGB / 255
plt.figure(figsize=(8, 8))
plt.subplot(1, 2, 1)
plt.title('Orgin Image')
plt.imshow(RGB)
plt.axis("off")
plt.subplot(1, 2, 2)
plt.title('Gray Image')
plt.imshow(new_RGB, cmap='gray')
plt.axis("off")
结果如下
H×W×C: (2534, 3670, 3)
uint8
Out[2]:
(-0.5, 3669.5, 2533.5, -0.5)

四:通道
通道:通道用来存储一张图像的颜色信息,或者说颜色代码。例如RGB模式,计算机内部在显式图像时,会将其分为三个通道,每个通道记录对应的灰度信息,然后交给计算机处理,最终显示出颜色
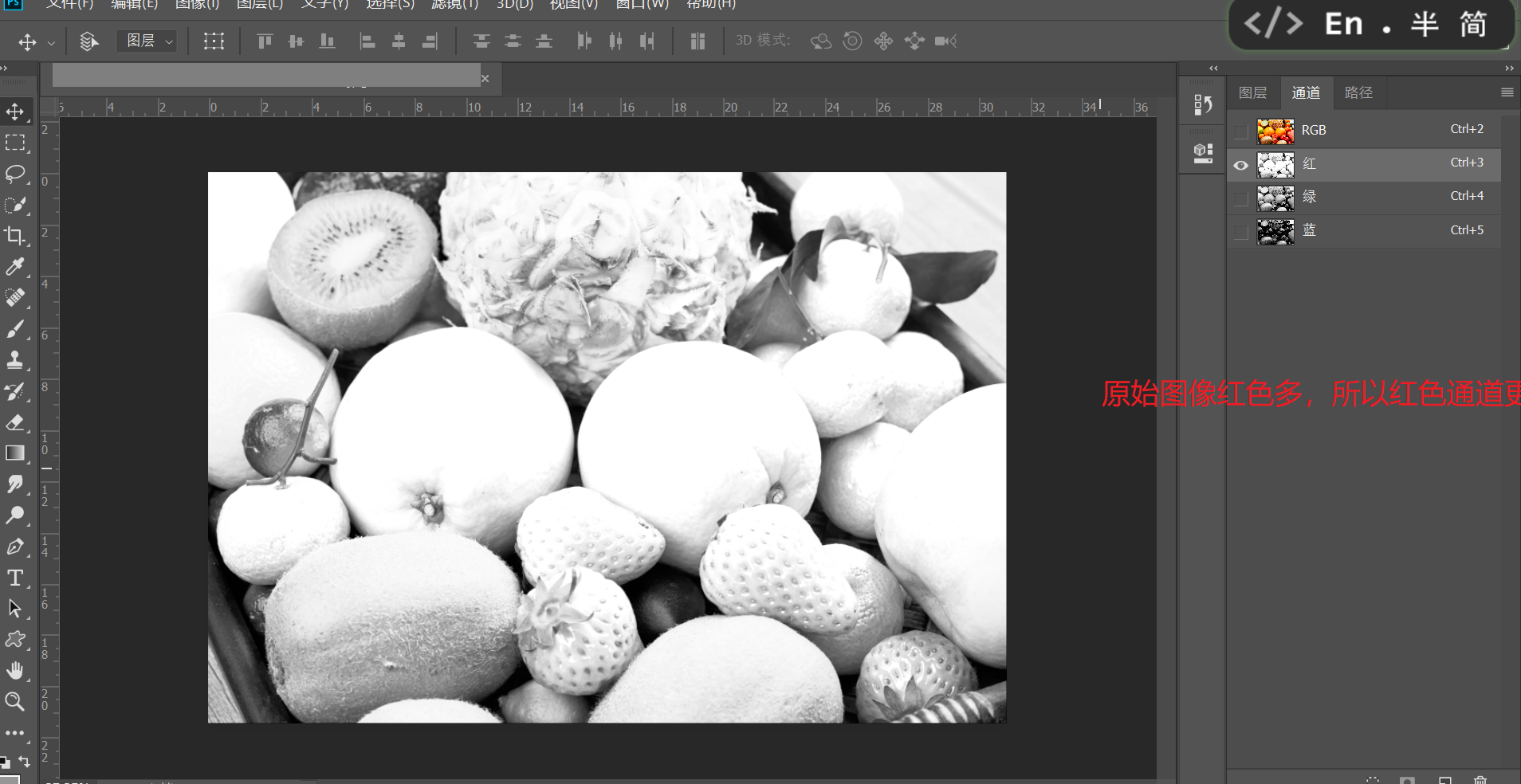
一张图像在给出时,除了必要高(H)宽(W)信息外,还会有一个通道信息(C),在处理图像时我们拿到的实际上是一个三维tensor,格式为H×W×C,对于RGB图像来说,这里的C就是3,所以说它实际上是3个H×W的图像进行堆叠
- 注意:在进行图像显示时C的含义很明确,就是3,分别表示三个通道颜色信息,而在CNN中,这里的C数目就不一定了,有可能会比3大很多,它是一个抽象的概念,在经过卷积后,所表示的含义十分抽象,不是我们能够理解的

如下,利用OpenCV拿到三个通道的tensor
import cv2 as cv
import matplotlib.pyplot as plt
image = cv.imread('./image/fruit.jpg')
RGB = cv.cvtColor(image, cv.COLOR_BGR2RGB)
print("H×W×C:", RGB.shape)
R = RGB.copy() # 红色
G = RGB.copy() # 绿色
B = RGB.copy() # 蓝色
# 只显示红色通道
R = R[:, :, 0]
# 只显示绿色通道
G = G [:, :, 1]
# 只显示蓝色通道
B = B [:, :, 2]
# 或者这样写
# (R, G, B) = cv.split(RGB)
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.title('Orgin Image')
plt.imshow(RGB)
plt.axis("off")
plt.subplot(2, 2, 2)
plt.title('Red')
plt.imshow(R, cmap='gray')
plt.axis("off")
plt.subplot(2, 2, 3)
plt.title('Green')
plt.imshow(G, cmap='gray')
plt.axis("off")
plt.subplot(2, 2, 4)
plt.title('Blue')
plt.imshow(B, cmap='gray')
plt.axis("off")
结果如下
H×W×C: (2534, 3670, 3)
Out[3]:
(-0.5, 3669.5, 2533.5, -0.5)

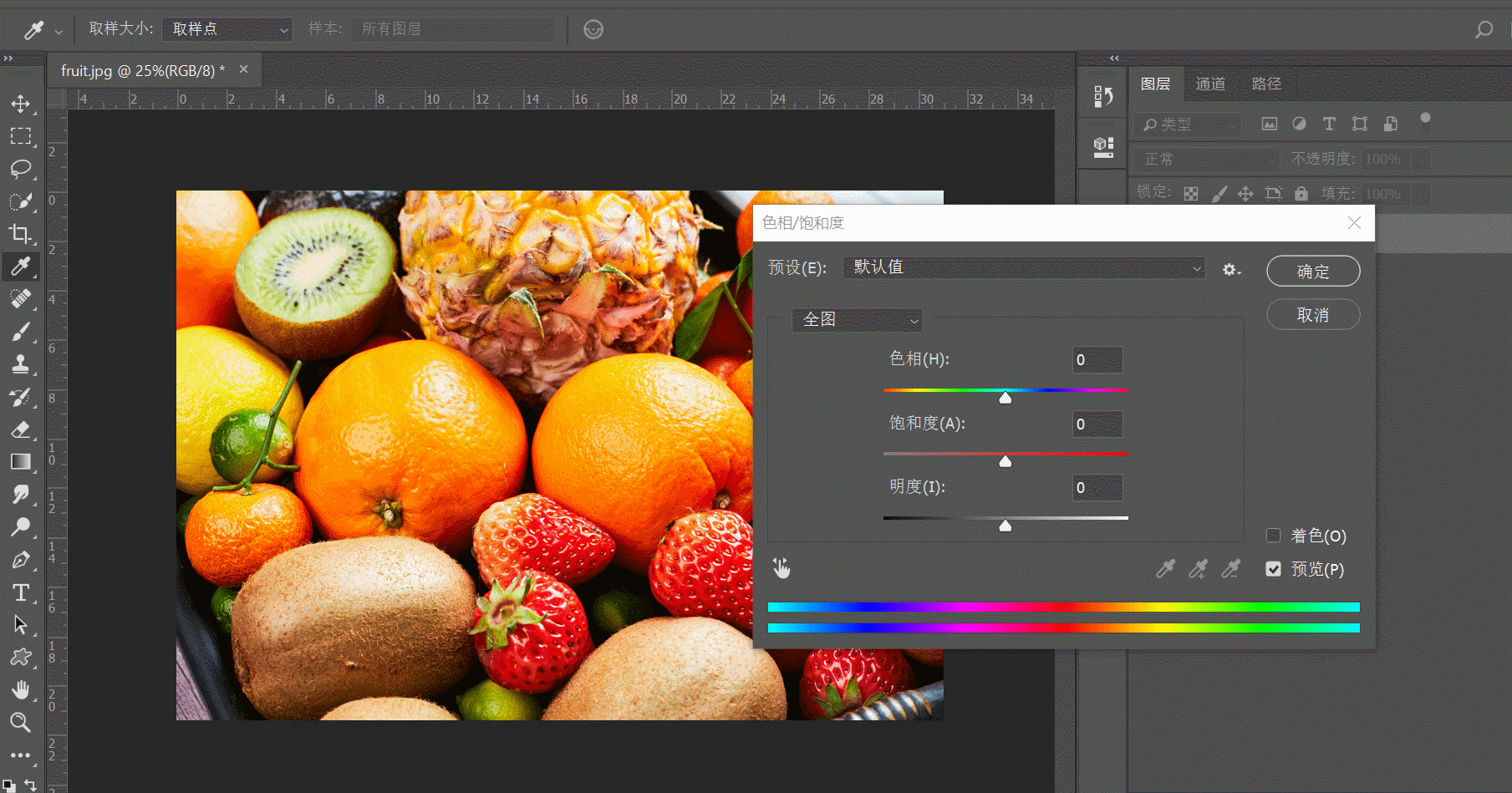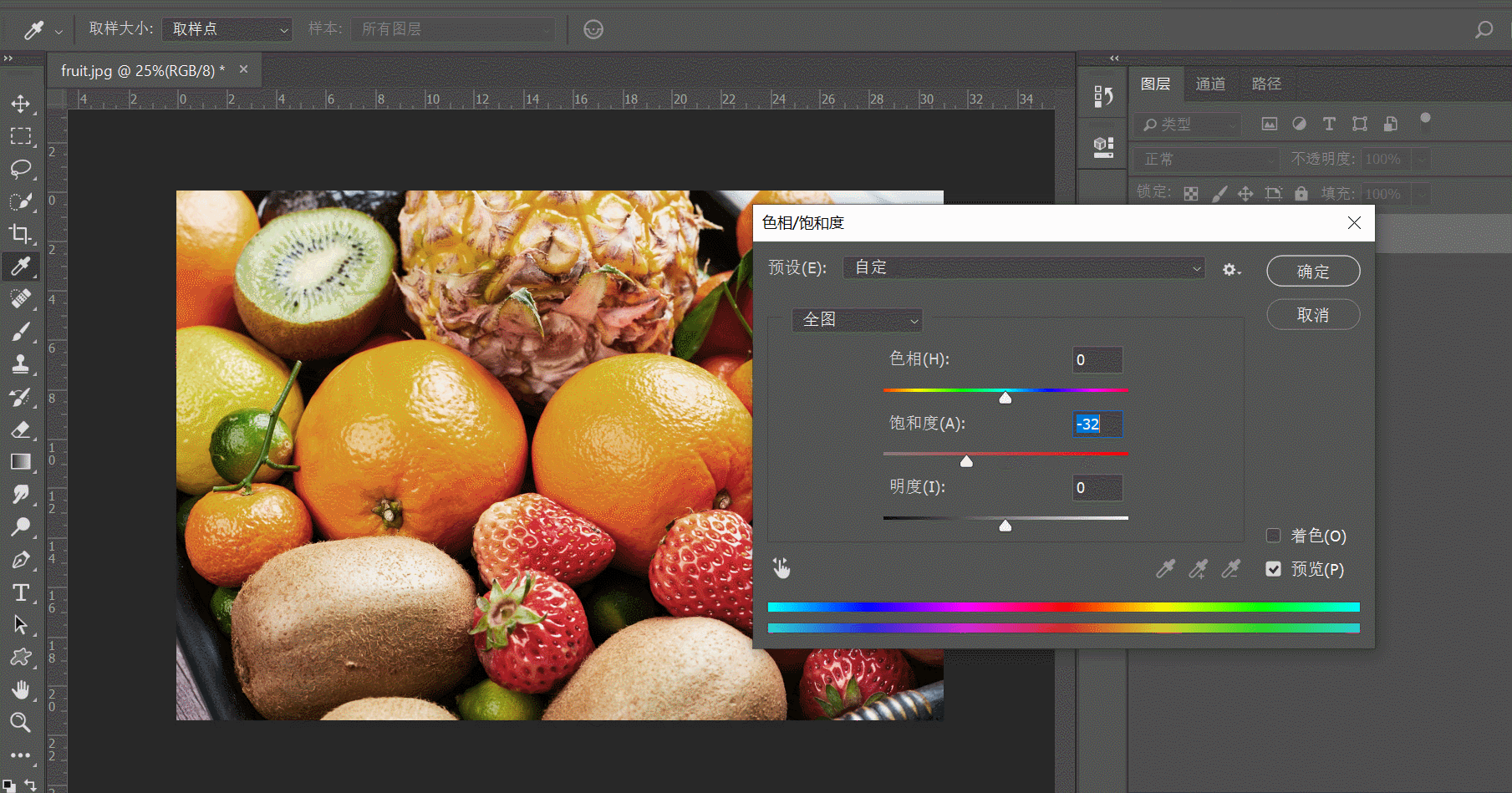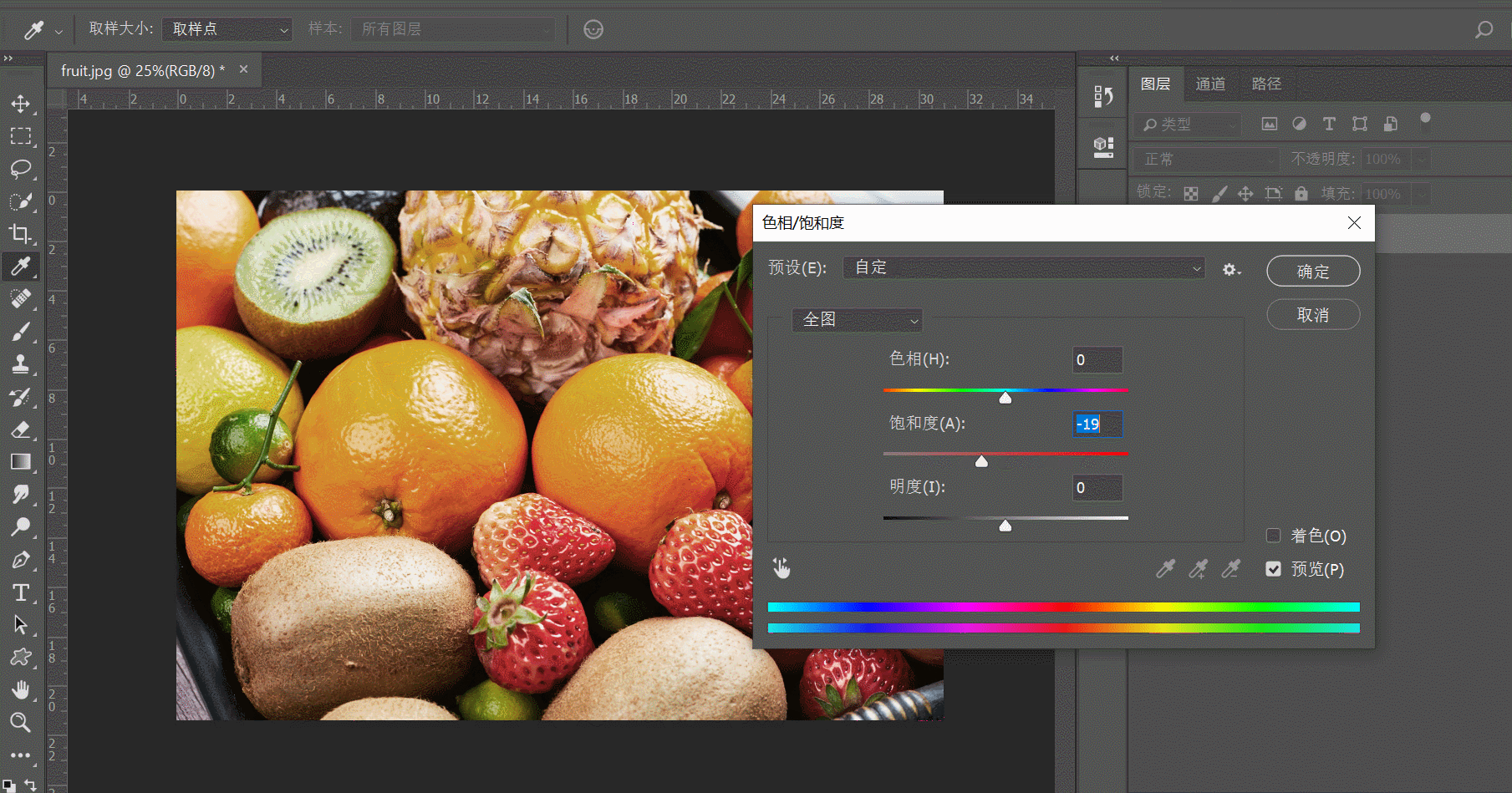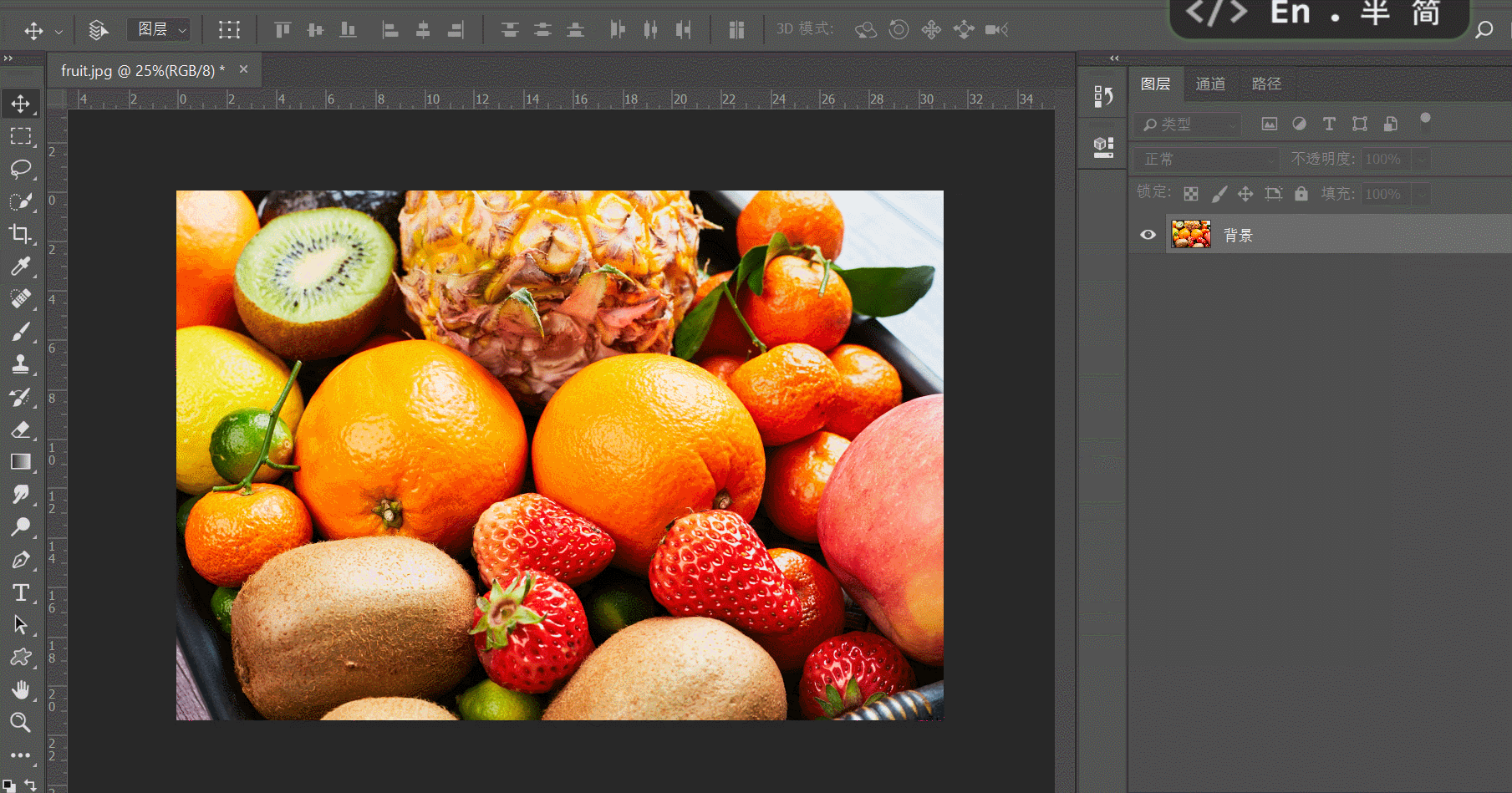
五:亮度、对比度和饱和度
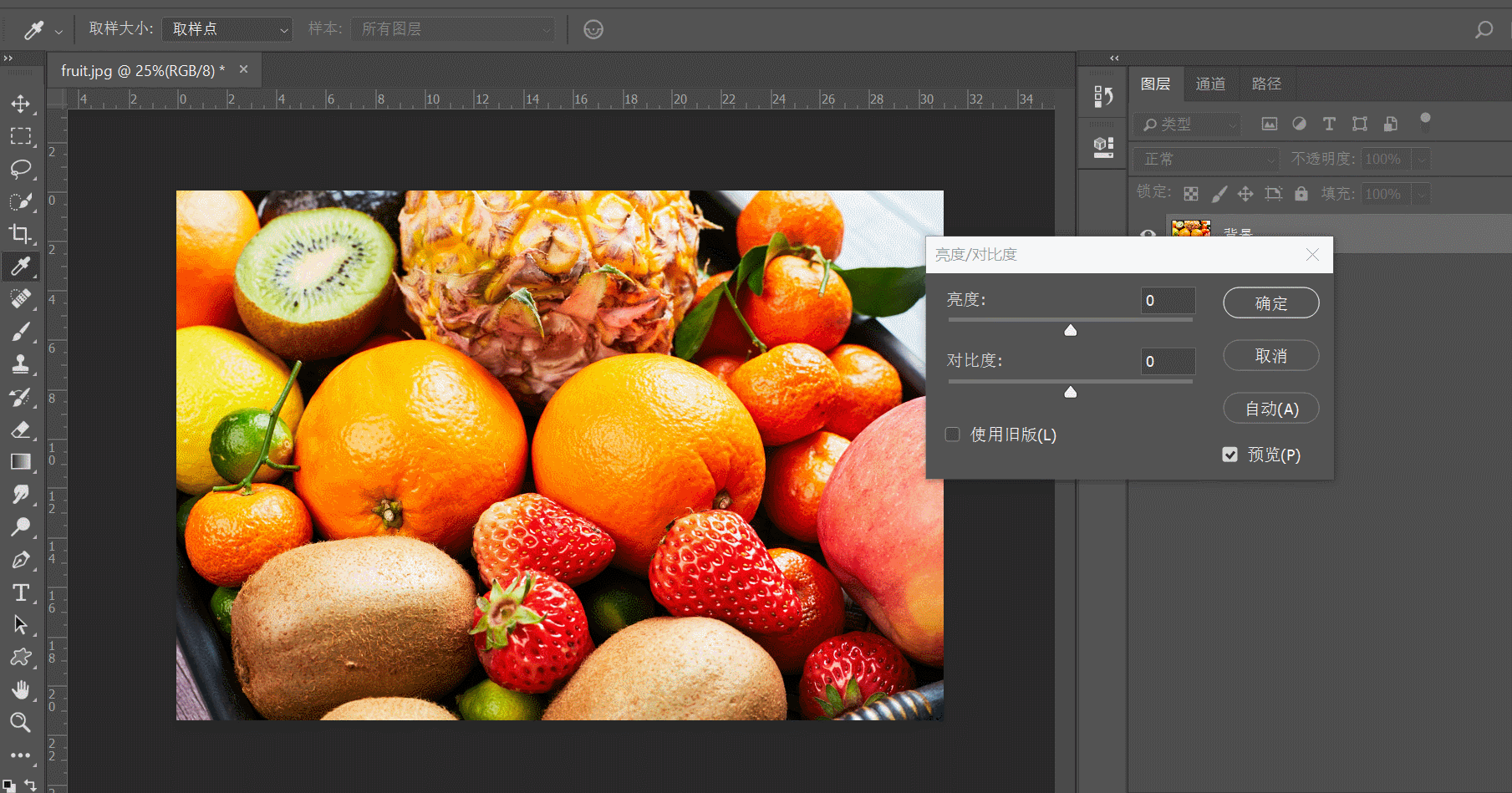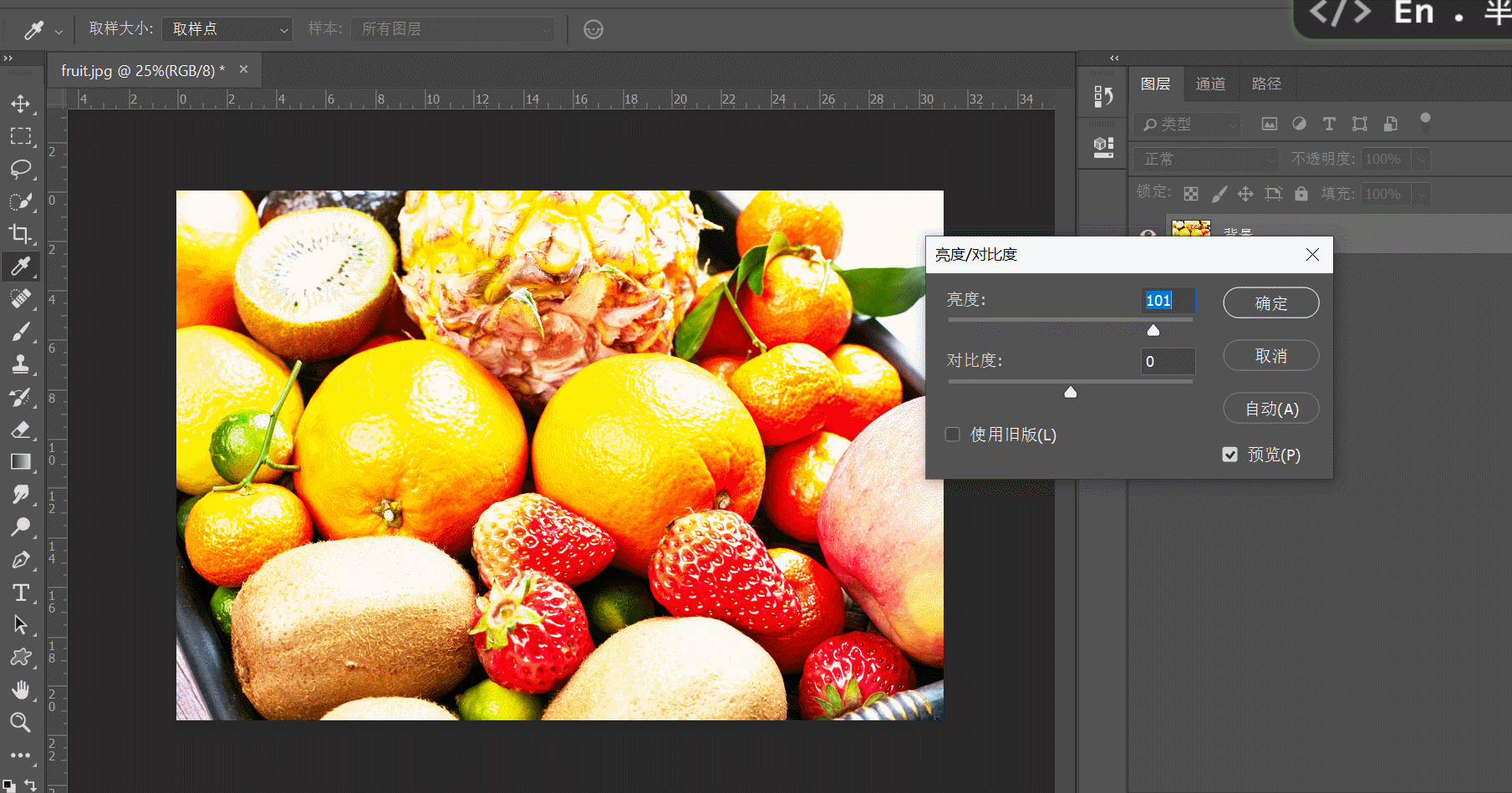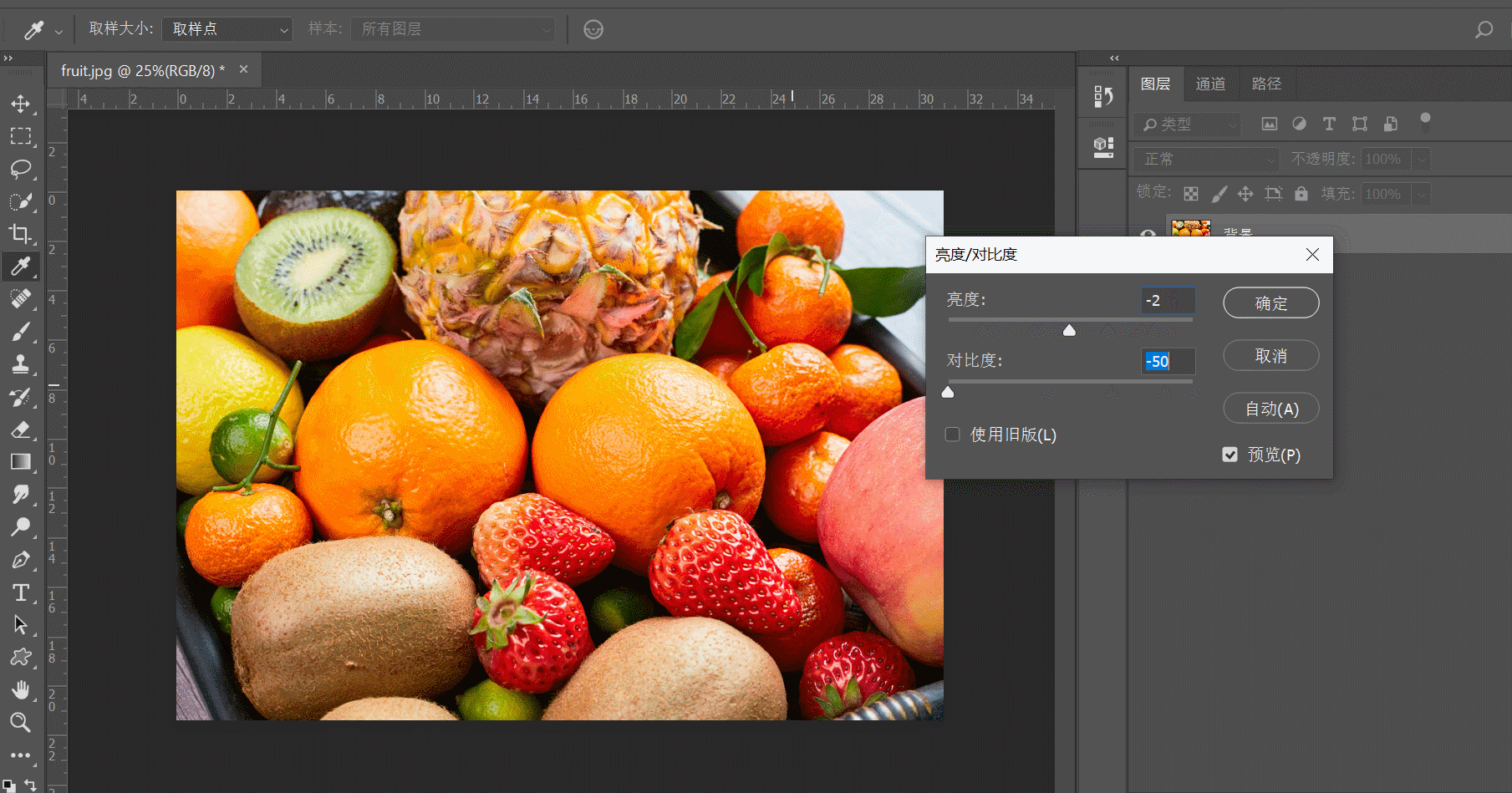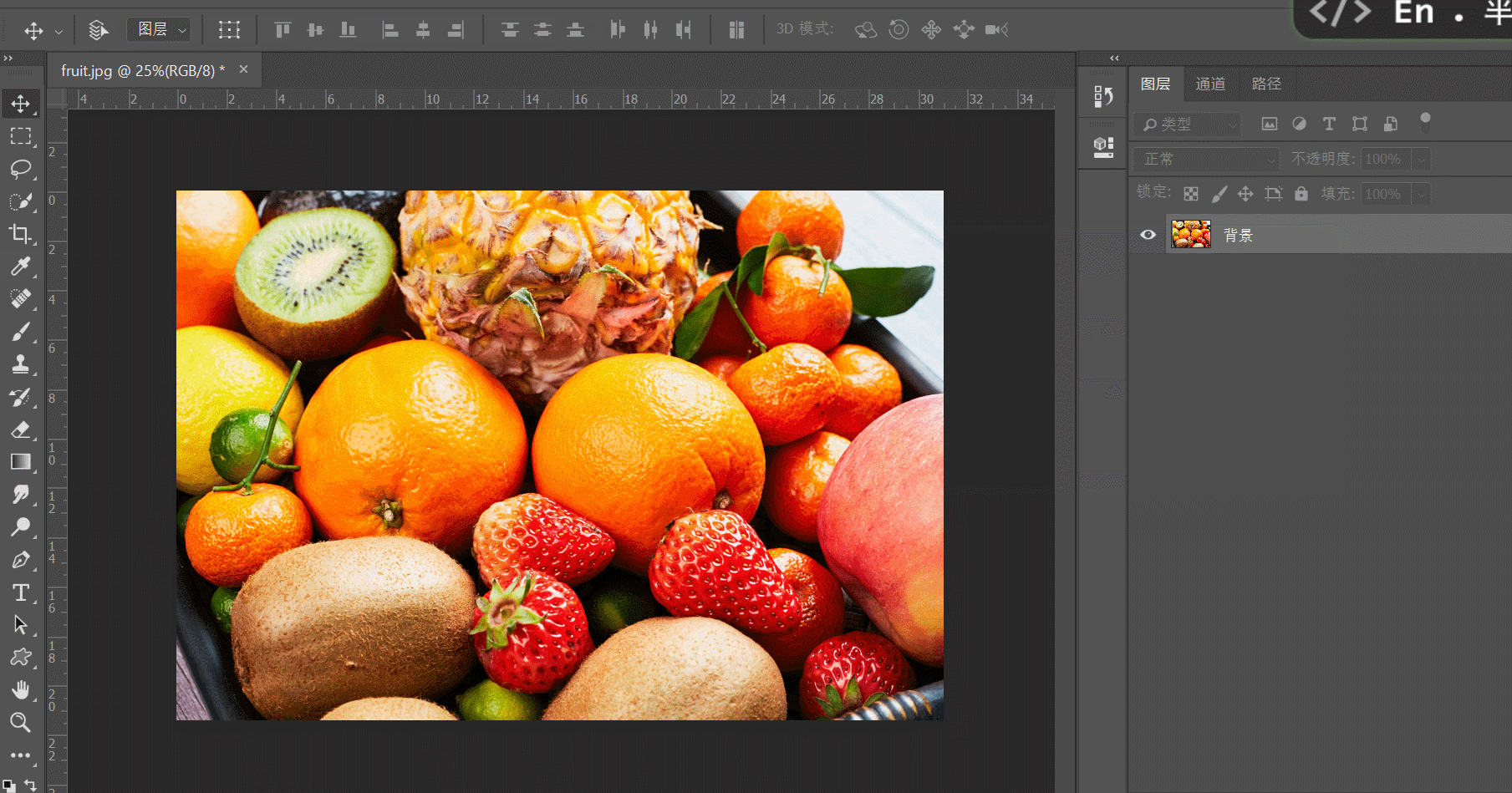
- 亮度:表示图像的明亮程度,在灰度图中,最高值对应白色,最低值对应黑色
- 对比度:表示亮和暗的差距,也即图像最大灰度级和最小灰度级之间的差值,这个差值越大对比就越大
- 饱和度:表示图像颜色种类的多少,饱和度越高颜色种类越多,图像也就越鲜艳
六:图像平滑和锐化
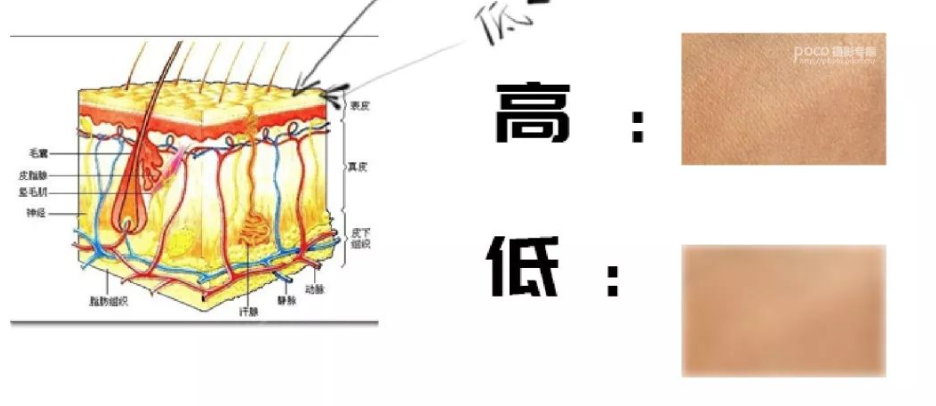
(1)图像平滑
图像平滑:图像平滑是指抑制高频部分(噪声),保留低频部分(连续色块),使图像亮度平缓渐变,减小突变梯度,改善图像质量
- 均值滤波:输出像素值是核窗口内像素值的 均值 ( 所有像素加权系数相等)
- 高斯滤波:最有用的滤波器 (尽管不是最快的)。 高斯滤波是将输入数组的每一个像素点与 高斯内核 卷积将卷积和当作输出像素值
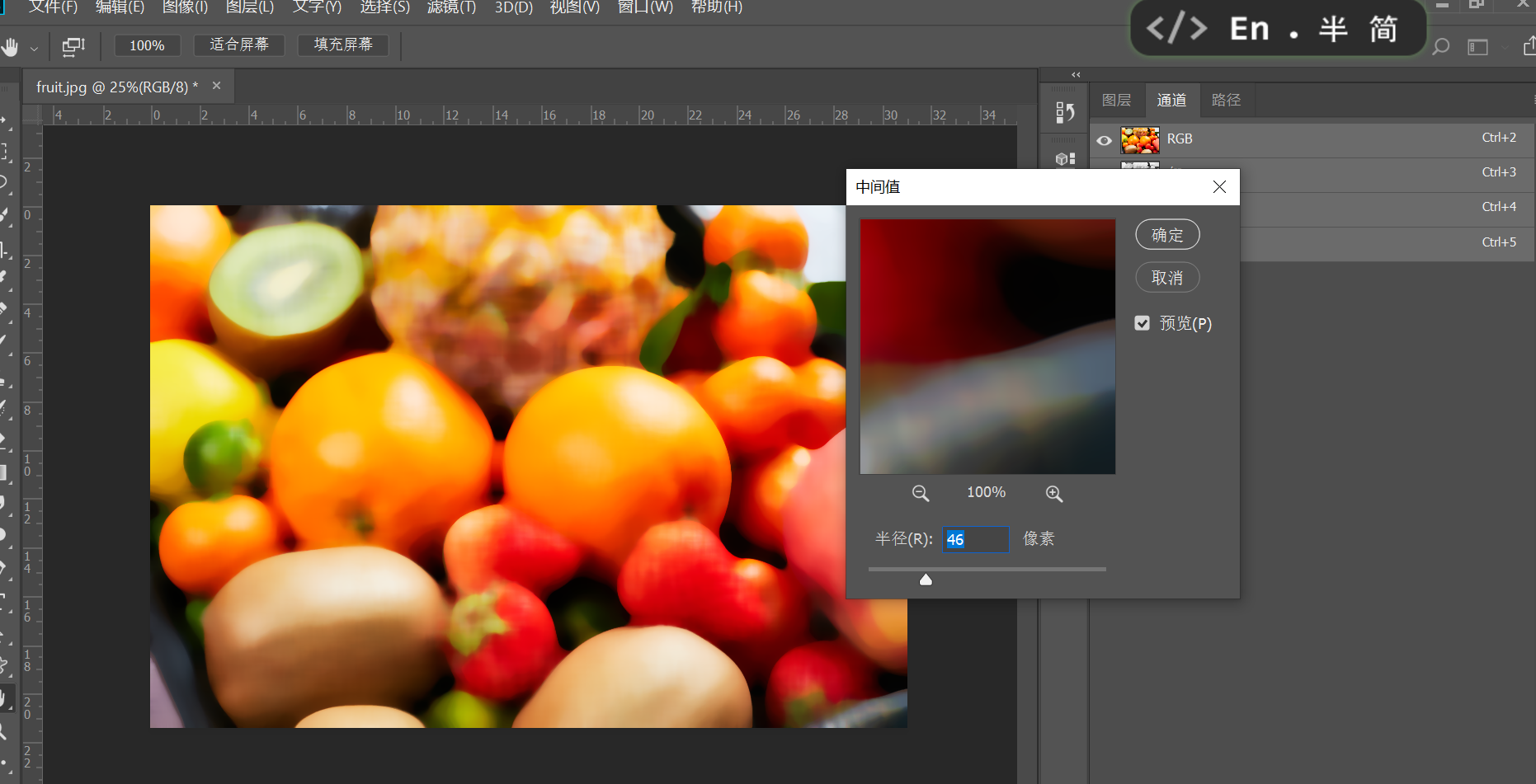
- 中值滤波:基本原理是把图像或序列中心点位置的值用该域的中值替代,具有运算简单、速度快、除噪效果好等优点,曾被认为是非线性滤波的代表
- 双边滤波:目前我们了解的滤波器都是为了 平滑 图像, 问题是有些时候这些滤波器不仅仅削弱了噪声, 连带着把边缘也给磨掉了。 为避免这样的情形 (至少在一定程度上 ), 我们可以使用双边滤波

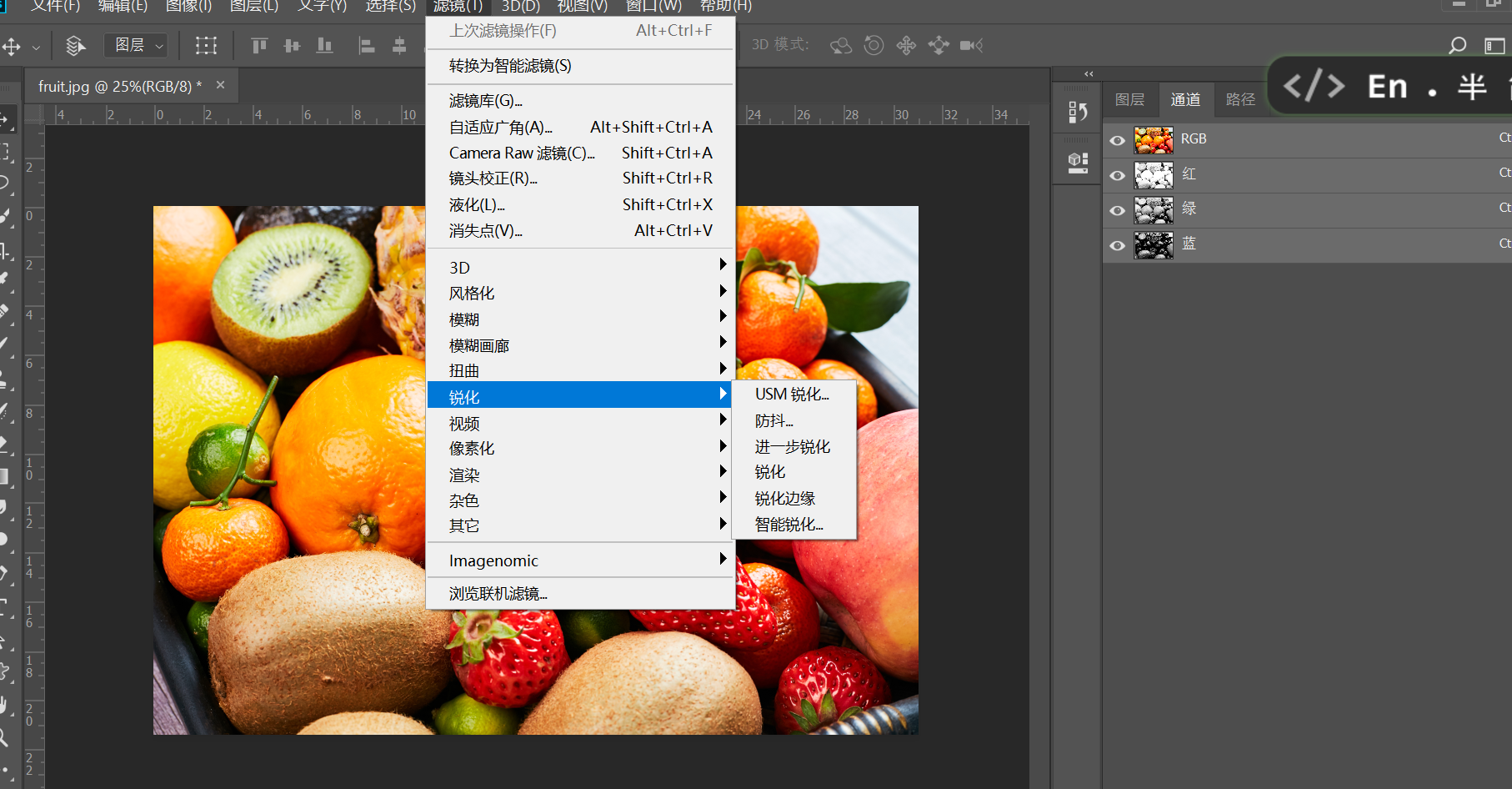
(2)图像锐化
图像锐化:与图像平滑相反,图像锐化会增强高频部分,减少模糊,但同时噪声也会被增强,使轮廓和边缘变得明显,增强灰度方差,便于后期识别和处理
- 微分法
- 高通滤波法

七:图像边缘提取
图像边缘提取:图像边缘是图像的最基本特征,所谓边缘指的是图像局部特性的不连续性,例如灰度的突变、颜色的突变或纹理结构的突变等等,边缘时一个区域的结束,也是另一个区域的开始
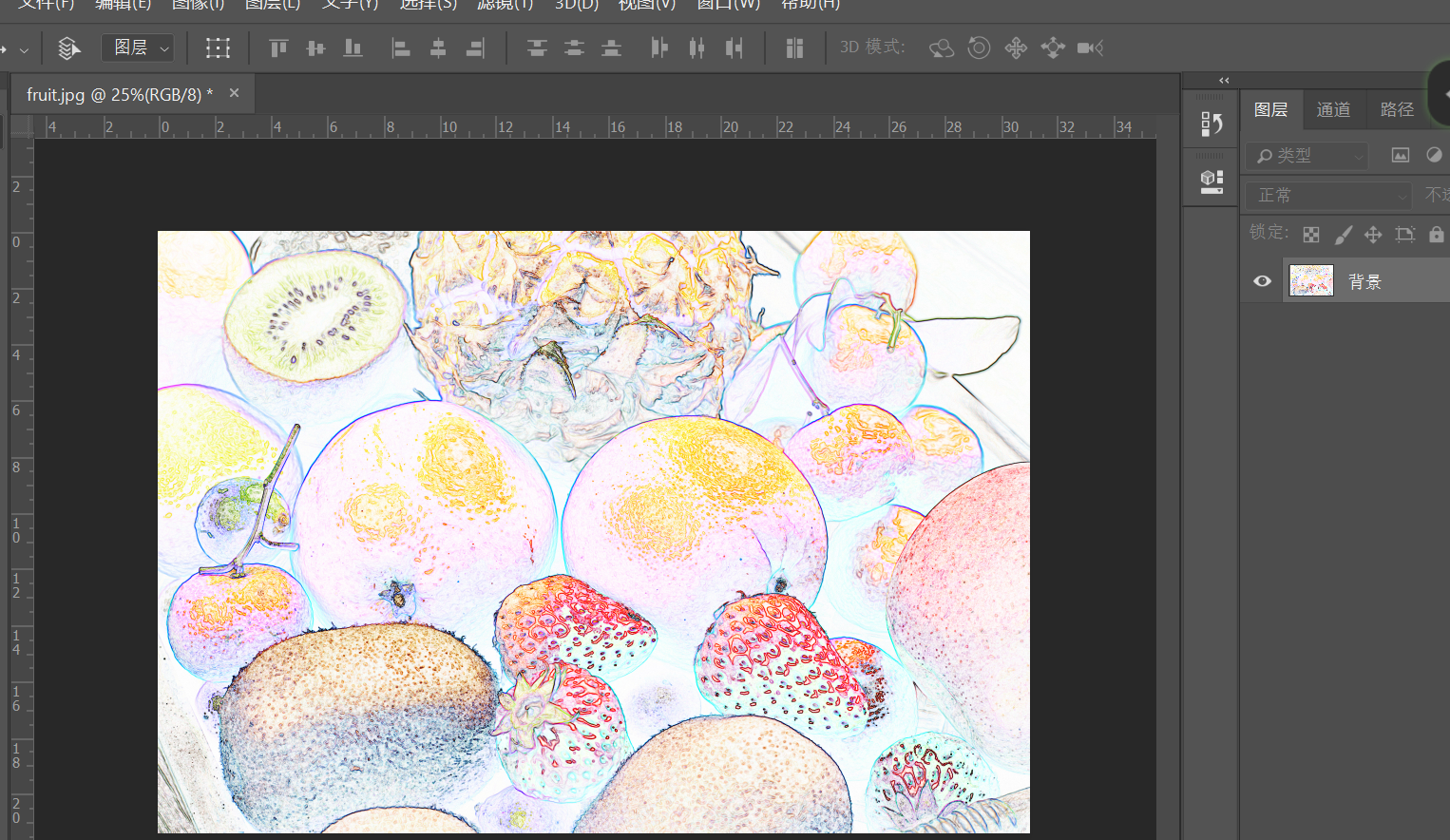
在计算图像边缘时,可以利用梯度的方法,要得到一副图像的梯度,则要求在每个像素点位置处计算偏导数
∂ f ( x , y ) ∂ x = lim x → 0 f ( x + ϵ ) − f ( x , y ) ϵ \frac{ \partial f(x, y) }{ \partial x } = \mathop{}\lim_{ x \to 0 } \frac{f(x+\epsilon)-f(x,y)}{\epsilon} ∂x∂f(x,y)=x→0limϵf(x+ϵ)−f(x,y)
∂ f ( x , y ) ∂ x = lim x → 0 f ( x + ϵ ) − f ( x , y ) ϵ \frac{ \partial f(x, y) }{ \partial x } = \mathop{}\lim_{ x \to 0 } \frac{f(x+\epsilon)-f(x,y)}{\epsilon} ∂x∂f(x,y)=x→0limϵf(x+ϵ)−f(x,y)
基于上述思想,就有如下集中边缘提取算子
- sobel算子:1.Sobel算子原理解析
- Perwitt算子
- Roberts算子
- Canny算子
- Laplacian算子
- …

八:形态学运算
形态学运算:形态学运算是针对二值图像依据数学形态学的集合论方法发展起来的图像处理方法
- 腐蚀:腐蚀的效果是把图片”变瘦”,其原理是在原图的小区域内取局部最小值
- 膨胀: 膨胀与腐蚀相反,取的是局部最大值,效果是把图片”变胖
- 开运算:先腐蚀后膨胀(因为先腐蚀会分开物体,这样容易记住),可以分离物体消除小区域
- 闭运算:先膨胀后腐蚀(先膨胀会使白色的部分扩张,以至于消除/“闭合”物体里面的小黑洞)
- 形态学梯度:膨胀图减去腐蚀图,得到轮廓图
- 顶帽:原图减去开运算后的图
- 黑帽:闭运算后的图减去原图