一、AcWing 4455. 出行计划（简单）

题目描述

最近西西艾弗岛上出入各个场所都要持有一定时限内的核酸检测阴性证明。
具体来时，如果在 $t$ 时刻做了核酸检测，则经过一段时间后可以得到核酸检测阴性证明。
这里我们假定等待核酸检测结果需要 $k$ 个单位时间，即在 $t+k$ 时刻可以获得结果。
如果一个场所要求持 $24$ 个单位时间内核酸检测结果入内，那么凭上述的核酸检测结果，可以在第 $t+k$ 时刻到第 $t+k+23$ 时刻进入该场所。
小 $C$ 按时间顺序列出接下来的 $n$ 项出行计划，其中第 $i$ 项（$1\le i\le n$）可以概括为：$t_i$ 时刻进入某场所，该场所需持有 $c_i$ 个单位时间内的核酸检测结果入内，其中 $0<c_i\le 2\times 10^5$。
为了合理安排核酸检测时间，试根据小 $C$ 的出行计划，回答如下查询：
如果在 $q$ 时刻做了核酸检测，有多少项出行计划的核酸检测要求可以得到满足？
这样的查询共有 $m$ 个，分别为 $q_1，q_2，\cdots ，q_m$；查询之间互不影响。

输入格式

输入的第一行包含空格分隔的三个正整数 $n$、$m$ 和 $k$，分别表示出行计划数目、查询个数以及等待核酸检测结果所需时间。
接下来输入 $n$ 行，其中每行包含用空格分隔的两个正整数 $t_i$、$c_i$，表示一项出行计划；出行计划按时间顺序给出，满足 $0<t_1\le t_2\le \cdots \le t_n\le 2\times 10^5$。
最后输入 $m$ 行，每行仅包含一个正整数 $q_i$，表示一个查询。$m$ 个查询亦按照时间顺序给出，满足 $0<q_1<q_2<\cdots <q_m\le 2\times 10^5$。

输出格式

输出共 m 行，每行一个整数，表示对应查询的答案。

数据范围

40% 的测试数据满足 $0<n，k\le 1000、m=1$；
70% 的测试数据满足 $0<n，m，k\le 1000$；
全部的测试数据满足 $0<n，m，k\le 10^5$。

输入样例

6 2 10
5 24
10 24
11 24
34 24
35 24
35 48
1
2

输出样例

3
3

样例解释

时刻 $1$ 做检测，可以满足第三、四、六项出行计划；
时刻 $2$ 做检测，可以满足第四、五、六项出行计划。

具体实现

1. 实现思路

• 如果在 $t$ 时刻做核酸，那么会在 $t+k$ 时刻得到核酸结果。
• 如果一个场所要求有 $c_i$ 时间内的核酸结果，那么可以在 $t+k$ 到 $t+k+c_i-1$ 的时间段内进入该场所。
• 我们在 $q_i$ 时刻开始做核酸，那么就可以在 $q_i+k$ 到 $q_i+k+c_i-1$ 之间进入场所，也就是要满足 $q_i+k\le t_i\le q_i+k+c_i-1$。
• 因此，便可以求出 $q_i$ 的取值范围，也就是 $t_i-k-c_i+1\le q_i\le t_i-k$，直接判断 $q_i$ 是否在该范围内即可。
• 对某一个出行计划进行判断，如果可行的话就是在这个区间内全部加 1（差分）。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 200010;

int n, m, k;
int b[N];

int main()
{
    cin >> n >> m >> k;
    //n个场所
    while (n -- )
    {
        int t, c;
        cin >> t >> c;
        int l = t - k - c + 1, r = t - k;
        //差分
        if (r > 0) 
        {
            b[max(1, l)] ++, b[r + 1] -- ;
        }
    }

    for (int i = 1; i < N; i ++ ) 
    {
        b[i] += b[i - 1];
    }

    //m个询问
    while (m -- )
    {
        int t;
        cin >> t;
        cout << b[t] << endl;
    }

    return 0;
}

二、AcWing 4510. 寻宝！大冒险！（简单）

题目描述

暑假要到了。
可惜由于种种原因，小 $P$ 原本的出游计划取消。
失望的小 $P$ 只能留在西西艾弗岛上度过一个略显单调的假期……直到……
某天，小 $P$ 获得了一张神秘的藏宝图。
西西艾弗岛上种有 $n$ 棵树，这些树的具体位置记录在一张绿化图上。
简单地说，西西艾弗岛绿化图可以视作一个大小为 $(L+1)\times (L+1)$ 的 $01$ 矩阵 $A$，地图左下角（坐标 $(0,0)$）和右上角（坐标 $(L,L)$）分别对应 $A[0][0]$ 和 $A[L][L]$。
其中 $A[i][j]=1$ 表示坐标 $(i,j)$ 处种有一棵树，$A[i][j]=0$ 则表示坐标 $(i,j)$ 处没有树。
换言之，矩阵 $A$ 中有且仅有的 $n$ 个 $1$ 展示了西西艾弗岛上 $n$ 棵树的具体位置。
传说，大冒险家顿顿的宝藏就埋藏在某棵树下。
并且，顿顿还从西西艾弗岛的绿化图上剪下了一小块，制作成藏宝图指示其位置。
具体来说，藏宝图可以看作一个大小为 $(S+1)\times (S+1)$ 的 $01$ 矩阵 $B$（$S$ 远小于$L$），对应着 $A$ 中的某一部分。
理论上，绿化图 $A$ 中存在着一处坐标 $(x,y)（0\le x,y\le L-S）$与藏宝图 $B$ 左下角 $(0,0)$ 相对应，即满足：
对 $B$ 上任意一处坐标 $(i,j)（0\le i,j\le S）$，都有 $A[x+i][y+j]=B[i][j]$。
当上述条件满足时，我们就认为藏宝图 $B$ 对应着绿化图 $A$ 中左下角为 $(x,y)$、右上角为 $(x+S,y+S)$ 的区域。
实际上，考虑到藏宝图仅描绘了很小的一个范围，满足上述条件的坐标 $(x,y)$ 很可能存在多个。
请结合西西艾弗岛绿化图中 $n$ 棵树的位置，以及小 $P$ 手中的藏宝图，判断绿化图中有多少处坐标满足条件。
特别地，藏宝图左下角位置一定是一棵树，即 $A[x][y]=B[0][0]=1$，表示了宝藏埋藏的位置。

输入格式

输入的第一行包含空格分隔的三个正整数 $n$、$L$ 和 $S$，分别表示西西艾弗岛上树的棵数、绿化图和藏宝图的大小。
由于绿化图尺寸过大，输入数据中仅包含 $n$ 棵树的坐标而非完整的地图；即接下来 $n$ 行每行包含空格分隔的两个整数 $x$ 和 $y$，表示一棵树的坐标，满足 $0\le x,y\le L$ 且同一坐标不会重复出现。
最后 $(S+1)$ 行输入小 $P$ 手中完整的藏宝图，其中第 $i$ 行$（0\le i\le S）$包含空格分隔的$ (S+1)$ 个 $0$ 和 $1$，表示 $B[S-i][0]\cdots B[S-i][S]$。
需要注意，最先输入的是 $B[S][0]\cdots B[S][S]一行，B[0][0]\cdots B[0][S]$ 一行最后输入。

输出格式

输出一个整数，表示绿化图中有多少处坐标可以与藏宝图左下角对应，即可能埋藏着顿顿的宝藏。

数据范围

40% 的测试数据满足：$L\le 50$；
70% 的测试数据满足：$L\le 2000$；
全部的测试数据满足：$n\le 1000、L\le 10^9$ 且 $S\le 50$。

输入样例 1

5 100 2
0 0
1 1
2 2
3 3
4 4
0 0 1
0 1 0
1 0 0

输出样例 1

3

样例 1 解释

绿化图上 $(0,0)、(1,1)$ 和 $(2,2)$ 三处均可能埋有宝藏。

输入样例 2

5 4 2
0 0
1 1
2 2
3 3
4 4
0 0 0
0 1 0
1 0 0

输出样例 2

0

样例 2 解释

如果将藏宝图左下角与绿化图 $(3,3)$ 处对应，则藏宝图右上角会超出绿化图边界，对应不成功。

具体实现

1. 实现思路

• 用大矩阵 A 表示一个地方的地图，在 A 当中抠出一个小矩阵 B，A 中的元素是未知的，B 中的元素是已知的（两个矩阵只有 0 和 1 两种元素，0 表示空地，1 表示有一棵树）。
• A 的面积最大是 $10^9\ast 10^9$，B 的面积最大是 $50\ast 50$，其中最多有 1000 棵树，A 和 B 的左下角是 $(0,0)$。
• 已知 B 矩阵 $(0,0)$ 处是 1，求 A 和 B 有多少个树的位置是匹配的。
• 因为最多只有 1000 棵树，所以可以依次枚举 A 中树的位置，判断一下在 B 当中对应的位置是不是 1，在判断 A 和 B 中 1 的个数是否相同。
• 要注意 $B[S][0]\cdots B[S][S]一行，B[0][0]\cdots B[0][S]$ 一行最后输入，就是纵方向是 x，横方向是 y。

2. 实现代码

#include <bits/stdc++.h>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, M = 55, INF = 1e8;

//n表示树的数量，m表示A矩阵的边长，k表示B矩阵的边长
int n, m, k;
//树的存储
PII tree[N];
//B矩阵的存储
int b[M][M];

int main()
{
    cin >> n >> m >> k;
    //读入树的坐标
    for (int i = 0; i < n; i ++ )
    {
        cin >> tree[i].x >> tree[i].y;
    }
    
    //B中树的数量
    int tc = 0;   
    //读入B矩阵
    for (int i = k; i >= 0; i -- )
    {
        for (int j = 0; j <= k; j ++ )
        {
            cin >> b[i][j];
            tc += b[i][j];
        }
    }

    //res表示可以匹配的数量
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int sx = tree[i].x, sy = tree[i].y;
        //判断是否越界
        if (sx + k > m || sy + k > m)
        {
            continue;
        }
        //A中树的个数
        int cnt = 0;
        //枚举每一个树
        for (int j = 0; j < n; j ++ )
        {
            int x = tree[j].x, y = tree[j].y;
            //如果这棵树在A和B中
            if (x >= sx && x - sx <= k && y >= sy && y - sy <= k)
            {
                //判断B的对应位置
                if (!b[x - sx][y - sy])
                {
                    cnt = -INF;
                }
                else
                {
                    cnt ++ ;
                }
            }
        }
        if (cnt == tc)
        {
            res ++ ;
        }
    }

    cout << res << endl;
    return 0;
}

三、AcWing 3422. 左孩子右兄弟（中等）

题目描述

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。
换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。
给定一棵包含 $N$ 个结点的多叉树，结点从 $1$ 至 $N$ 编号，其中 $1$ 号结点是根，每个结点的父结点的编号比自己的编号小。
请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。
注：只有根结点这一个结点的树高度为 $0$。
例如如下的多叉树：

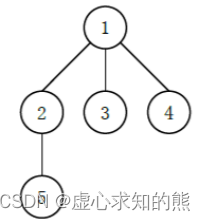
可能有以下 $3$ 种 (这里只列出 $3$ 种，并不是全部) 不同的 “左孩子右兄弟”表示：

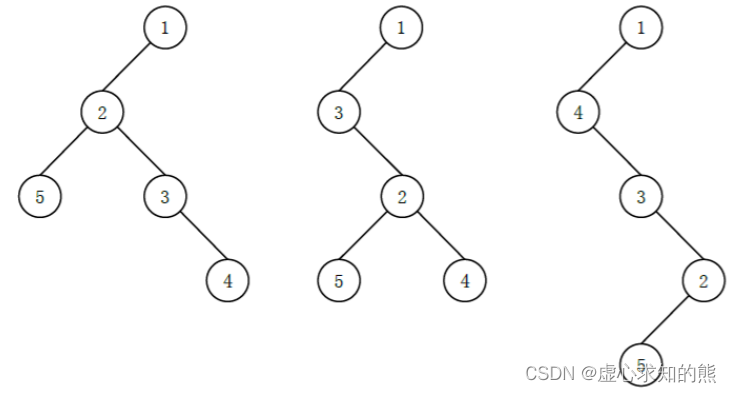
其中最后一种高度最高，为 $4$。

输入格式

输入的第一行包含一个整数 $N$。
以下 $N-1$ 行，每行包含一个整数，依次表示 $2$ 至 $N$ 号结点的父结点编号。

输出格式

输出一个整数表示答案。

数据范围

对于 30% 的评测用例，$1\le N\le 20$；
对于所有评测用例，$1\le N\le 10^5$。

输入样例

5
1
1
1
2

输出样例

4

具体实现

1. 实现思路

• 左边存孩子，右边存兄弟。
• 每棵树最大可能形成的高度是其最深子树的高度（根节点高度为 0）与其子树数量的和。
• 每棵子树的深度只跟这棵子树内部有关，与其它节点没有关系。
• 因此，只需求出两部分分别的最大值即可。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n;
int h[N], e[N], ne[N], idx;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++ ;
}

int dfs(int u)
{
    //hmax表示子树的最大高度
    //cnt表示子树的数量
    int hmax = 0, cnt = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        hmax = max(hmax, dfs(j));
        cnt ++ ;
    }
    return hmax + cnt;
}

int main()
{
    cin >> n;

    memset(h, -1, sizeof h);
    for (int i = 2; i <= n; i ++ )
    {
        int p;
        cin >> p;
        add(p, i);
    }

    cout << dfs(1) << endl;

    return 0;
}

四、AcWing 4728. 乘方 （简单）

题目描述

小文同学刚刚接触了信息学竞赛，有一天她遇到了这样一个题：给定正整数 $a$ 和 $b$，求 $a^b$ 的值是多少。
$a^b$ 即 $b$ 个 $a$ 相乘的值，例如 $2^3$ 即为 $3$ 个 $2$ 相乘，结果为 $2\times 2\times 2=8$。
“简单！”小文心想，同时很快就写出了一份程序，可是测试时却出现了错误。
小文很快意识到，她的程序里的变量都是 int 类型的。
在大多数机器上，int 类型能表示的最大数为 $2^{31}-1$，因此只要计算结果超过这个数，她的程序就会出现错误。
由于小文刚刚学会编程，她担心使用 int 计算会出现问题。
因此她希望你在 $a^b$ 的值超过 $10^9$ 时，输出一个$-1$ 进行警示，否则就输出正确的 $a^b$ 的值。
然而小文还是不知道怎么实现这份程序，因此她想请你帮忙。

输入格式

输入共一行，两个正整数 $a，b$。

输出格式

输出共一行，如果 $a^b$ 的值不超过 $10^9$，则输出 $a^b$ 的值，否则输出 -1。

数据范围

对于 10% 的数据，保证 $b=1$。
对于 30% 的数据，保证 $b\le 2$。
对于 60% 的数据，保证 $b\le 30，a^b\le 10^{18}$。
对于 100% 的数据，保证 $1\le a，b\le 10^9$。

输入样例 1

10 9

输出样例 1

1000000000

输入样例 2

23333 66666

输出样例 2

‐1

具体实现

1. 实现思路

• 此题比较简单，只需分情况讨论。
• 第一种情况，当 a=1 时，结果就是 1，就不用进入循环直接输出即可。
• 第二种情况，当 a＞1 时，进入循环，在中间要小心结果 res 超出范围，因此，res 使用 long long。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int main()
{
    int a, b;
    cin >> a >> b;

    LL res = 1;
    while (a > 1 && b -- )
    {
        res *= a;
        if (res > 1e9)
        {
            res = -1;
            break;
        }
    }

    cout << res << endl;
    return 0;
}

五、AcWing 4729. 解密（简单）

题目描述

给定一个正整数 $k$，有 $k$ 次询问，每次给定三个正整数 $n_i，e_i，d_i$，求两个正整数 $p_i，q_i$，使 $n_i=p_i\times q_i，e_i\times d_i=(p_i-1)(q_i-1)+1$。

输入格式

第一行一个正整数 $k$，表示有 $k$ 次询问。
接下来 $k$ 行，第 $i$ 行三个正整数 $n_i，d_i，e_i$。

输出格式

输出 $k$ 行，每行两个正整数 $p_i，q_i$ 表示答案。
为使输出统一，你应当保证 $p_i\le q_i$。
如果无解，请输出 NO。

数据范围

以下记 $m=n-e\times d+2$。
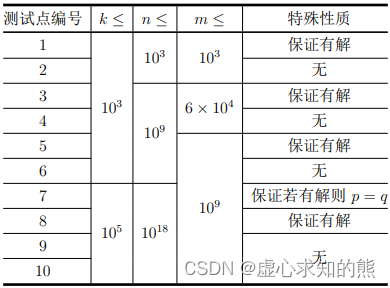
保证对于 100% 的数据，$1\le k\le 10^5$，对于任意的 $1\le i\le k，1\le n_i\le 10^{18}，1\le e_i\times d_i\le 10^{18}，1\le m\le 10^9$。

输入样例

10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109

输出样例

2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88

具体实现

1. 实现思路

• 首先，由 $n_i=p_i\times q_i，e_i\times d_i=(p_i-1)(q_i-1)+1$ 这两式进行公式的推导。
• 具体推导过程如下：

• 由上述推导过程，就可以使用伟达定理（二元一次方程）对 $p_i，q_i$ 进行求解。
• 这里需要注意的是，要先输出数据小的那一部分。
• 由于数据范围是 $10^{18}$，要使用 long long。
• 因为输出的结果必须是正整数，所以需要对 dt 是否为正整数进行判断。

2. 实现代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int main()
{
    int k;
    cin >> k;

    while (k -- )
    {
        LL n, d, e;
        cin >> n >> d >> e;
        LL m = n - e * d + 2;
        LL dt = m * m - 4 * n;
        //开根号
        LL r = sqrt(dt);

        //如果dt小于0，或者dt不是整数（因为输出的结果必须是正整数）
        if (dt < 0 || r * r != dt)
        {
            puts("NO");
        }
        else 
        {
            cout << (m - r) / 2 << " " << (m + r) / 2 << endl;
        }
    }

    return 0;
}