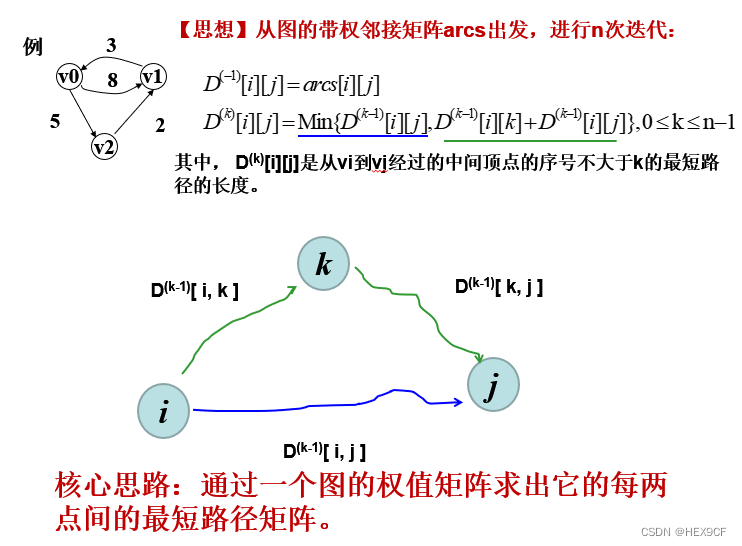
Floyd算法

for (int k = 0; k < n; k++) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (d[i][k] != INF && d[k][j] != INF) {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

Dijkstra算法（基于最小堆）

void dijkstra(int start) {
	vis.reset();
	// 初始化
	for (int i = 0; i < n; i++) {
		if (i == start) {
			dist[i] = 0;
			hmin.push({i, 0});
		} else {
			dist[i] = INF;
			prior[i] = -1;
		}
	}
	while (hmin.size()) {
		auto t = hmin.top();
		hmin.pop();
		int u = t.v;
		int du = t.d;
		if (vis[u]) {
			continue;
		}
		vis[u] = 1;
		// 访问邻接节点
		for (int i = head[u]; ~i; i = edge[i].next) {
			int v = edge[i].to;
			if (dist[v] > du + 1) {
				// 更新最短距离
				dist[v] = du + 1;
				prior[v] = u;
				hmin.push({v, du + 1});
			}
		}
	}
}

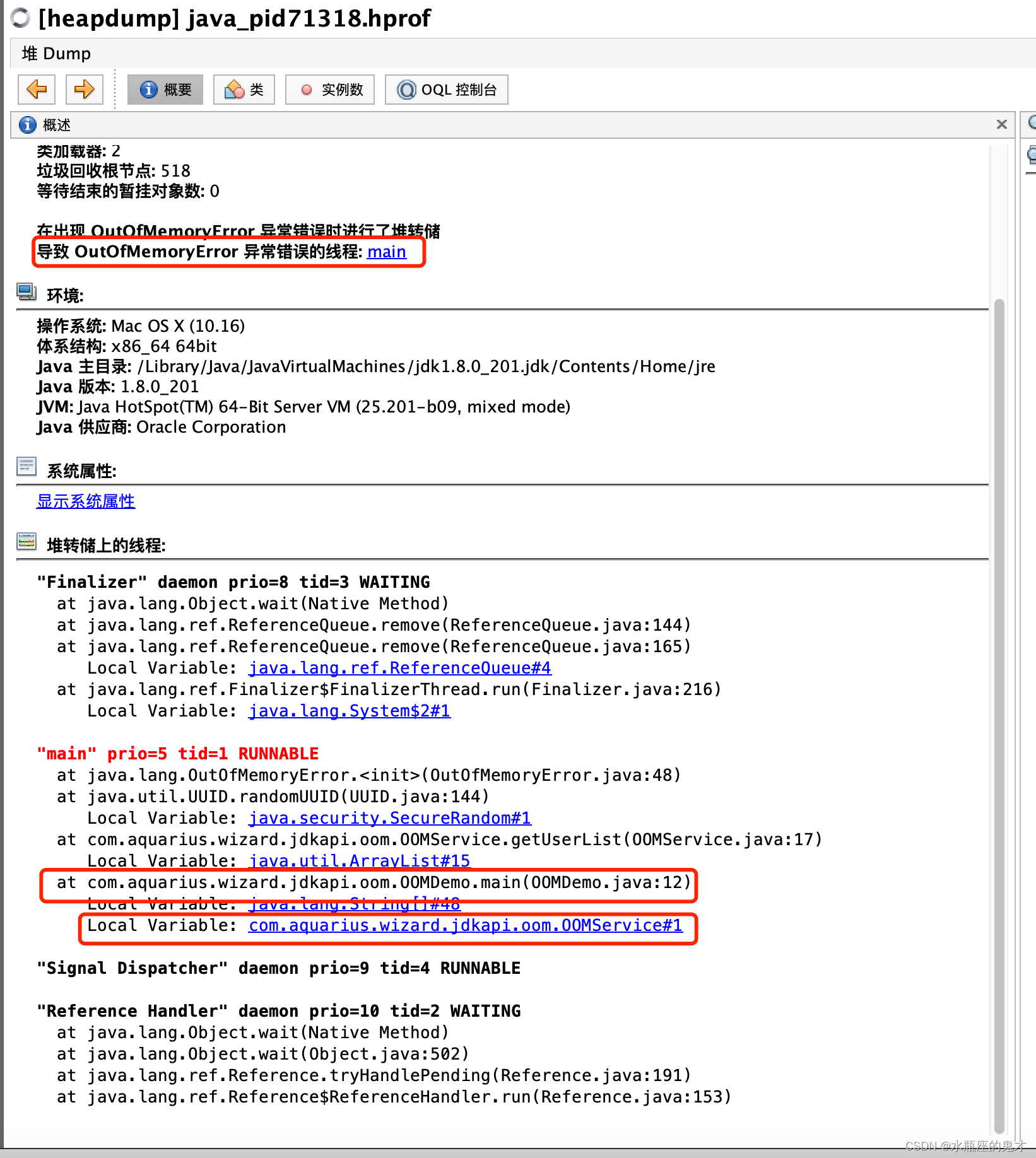
Dijkstra算法和弗洛伊德(Floyd)算法是如何求最短路径的？两种算法各自的优缺点是什么？

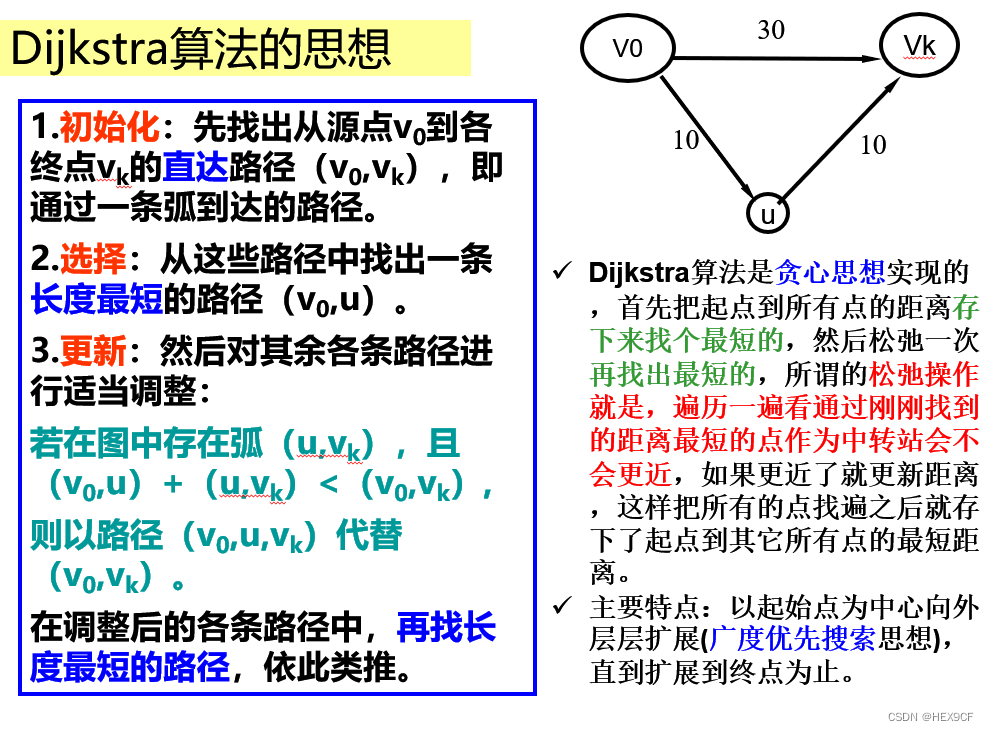
• Dijkstra算法：是一种单源最短路径算法，即从图中的一个节点到其他所有节点的最短路径。它的基本思想是每次找到离源节点最近的一个节点，然后以该节点为中心进行扩展，最终得到源节点到其他所有节点的最短路径。

  • 优点：当只需要求解单源最短路径问题时，效率较高。
  • 缺点：
    • 不能处理存在负权边的图。
    • 只能求解单源最短路径问题，不能求解多源最短路径问题。

• 弗洛伊德(Floyd)算法：是一种多源最短路径算法，即求图中任意两点之间的最短路径。它的基本思想是从 vi 到 vj 的所有可能存在的路径中，选出一条长度最短的路径。

  • 优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
  • 缺点：时间复杂度比较高，不适合计算大量数据。