1.引言
1.1.NRI研究的意义
在许多领域,如物理学、生物学和体育,我们遇到的系统都是由相互作用的组分构成的,这些组分在个体和整体层面上都产生复杂的动态。建模这些动态是一个重大的挑战,因为往往我们只能获取到个体的轨迹数据,而不知道其背后的相互作用机制或具体的动态模型。
以篮球运动员在球场上的运动为例,运动员的动态显然受到其他运动员的影响。作为观察者,我们能够推断出场上可能发生的各种交互,如防守、掩护等。然而,手动标注这些交互不仅繁琐,而且耗时。因此,一个更有前景的方法是在无监督的条件下学习这些底层的交互模式,这些模式可能在多种不同的任务中都具有通用性。
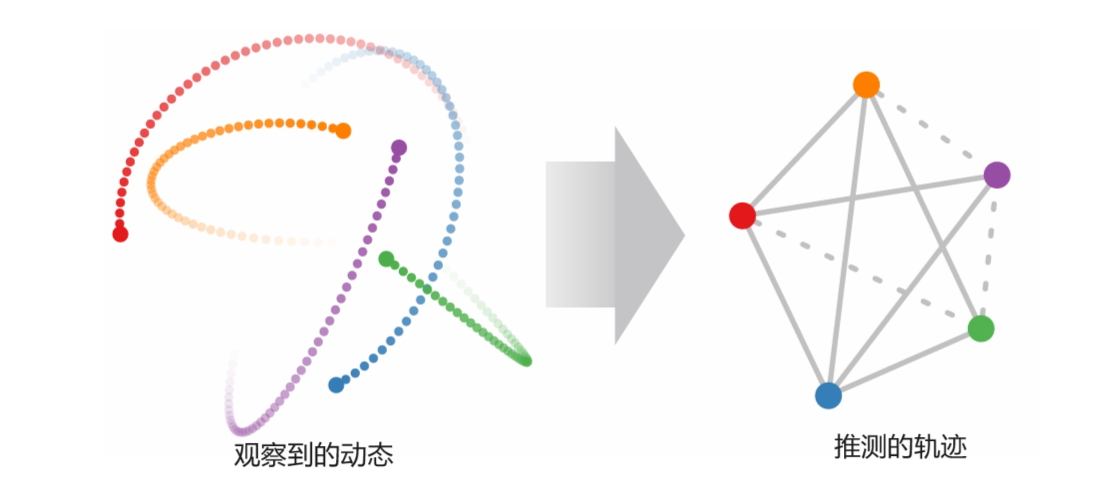
1.2.主要内容
本文将介绍一种基于图结构潜在空间的变分自编码器模型——神经关系推理(Neural Relational Inference)模型。这种模型在相关论文中被详细阐述,并配备了代码库以便于实现和实验。
神经关系推理模型旨在解决预测粒子运动轨迹的问题,特别是在存在未知粒子间相互作用的情况下。设想我们有一组粒子(例如带电粒子),它们因某种相互作用(如电磁力)而在空间中移动。我们观察到每个粒子在一段时间T内的运动轨迹,包括其位置和速度。每个粒子的新状态不仅由其当前状态决定,还受到其他粒子的影响。我们拥有一组粒子的轨迹数据,但粒子间的确切相互作用未知。
模型的目标是通过学习粒子的动态行为,基于已知的轨迹样本来预测未来的轨迹。如果已知粒子间的相互作用形式(即它们如何以图的形式相互连接),预测粒子的动态将更为直接。在这种理想情况下,每个粒子对应于图中的一个节点,而节点间的连接强度可以通过边的权重来表示。然而,在这个问题中,我们并没有获得这样的交互图。
因此,神经关系推理模型采用了变分自编码器的编码器部分,以从给定的轨迹数据中采样潜在的交互图。具体来说,编码器部分使用图神经网络(GNN)技术来捕捉粒子间的潜在关系,并生成一个能够代表这些关系的图结构。这个图结构随后被用作解码器部分的输入,以预测粒子的未来轨迹。
通过这种方式,神经关系推理模型能够同时学习粒子间的潜在交互和粒子的动态行为,从而实现更准确的轨迹预测。在训练过程中,模型通过最大化给定轨迹数据下的似然函数(即证据下界ELBO)来优化其参数,以使得生成的潜在交互图能够最好地解释和预测观察到的轨迹。
2.神经关系推理模型(NRI)原理
2.1.NRI的基本原理
神经关系推理(NRI)模型是一个专注于从观察到的轨迹中推断对象间相互作用和动态行为的模型。它由两个核心组件组成:编码器和解码器,这两个组件是联合训练的。
2.1.1.编码器:
编码器负责根据观察到的轨迹数据 x x x 来预测对象间的相互作用,即潜在的图结构 z z z。这里的轨迹数据 x x x 包括 N 个对象在 T 个时间步上的特征向量集合,具体地,我们用 x i t x^t_i xit 表示第 t 个时间点上对象 v i v_i vi 的特征向量(如位置和速度)。所有对象在时间点 t 的特征集合记作 x t = ( x 1 t , … , x N t ) x^t = (x^t_1, \ldots, x^t_N) xt=(x1t,…,xNt),而对象 v i v_i vi 的完整轨迹是 x i = ( x i 1 , … , x i T ) x_i = (x^1_i, \ldots, x^T_i) xi=(xi1,…,xiT)。
编码器 q ( z ∣ x ) q(z|x) q(z∣x) 的目标是输出一个分布,该分布描述了给定轨迹 x x x 下潜在图结构 z z z 的可能性。特别是, z i j z_{ij} zij 表示对象 v i v_i vi 和 v j v_j vj 之间的离散边类型,用于表示它们之间的交互类型。编码器使用 K 种可能的交互类型对 z i j z_{ij} zij 进行一位有效编码。
2.1.2.解码器:
解码器则基于编码器输出的潜在图结构 z z z 和已知的轨迹数据 x x x 来学习并预测对象的动态行为。具体来说,解码器通过以下公式定义:
p ( x ∣ z ) = ∏ t = 1 T p ( x t + 1 ∣ x t , x 1 , z ) p(x|z) = \prod_{t=1}^{T} p(x_{t+1}|x^t, x^1, z) p(x∣z)=t=1∏Tp(xt+1∣xt,x1,z)
它使用图神经网络(GNN)来模拟给定潜在图 z z z 和历史轨迹 x t x^t xt 下,下一个时间步 t + 1 t+1 t+1 的轨迹 x t + 1 x_{t+1} xt+1 的分布。
2.1.3.模型优化:
整个模型基于变分自编码器(VAE)框架进行优化,目标是最大化证据下界(ELBO):
L = E q ( z ∣ x ) [ log p ( x ∣ z ) ] − KL [ q ( z ∣ x ) ∣ ∣ p ( z ) ] L = \mathbb{E}_{q(z|x)}[\log p(x|z)] - \text{KL}[q(z|x) || p(z)] L=Eq(z∣x)[logp(x∣z)]−KL[q(z∣x)∣∣p(z)]
其中,KL 表示 Kullback-Leibler 散度,用于衡量两个概率分布之间的差异。先验 p ( z ) p(z) p(z) 假设边类型是均匀分布的,但也可以根据需要采用其他先验分布,比如鼓励稀疏图的先验。
NRI 模型通过编码器和解码器的联合训练,能够无监督地从观察到的轨迹中学习对象间的相互作用和动态行为,这对于理解复杂系统的运动规律和交互模式具有重要意义。
2.2.与VAE编码器的差异
与原始的变分自编码器(VAE)模型相比,我们的神经关系推理(NRI)模型确实存在几个显著的不同之处。以下是对这些差异的详细改写和描述:
-
多时间步预测:
在原始的VAE中,解码器通常被训练来根据潜在变量(z)重构单个数据点。然而,在我们的NRI模型中,为了捕捉系统动态的连续性和交互的长期影响,我们训练解码器来预测多个时间步的轨迹,而不仅仅是单个时间步。这种设置使得解码器在预测过程中能够充分利用潜在交互图(z)中的信息,从而避免了解码器忽略潜在变量(z)的问题。 -
离散潜在变量与连续松弛:
原始的VAE通常处理连续的潜在变量,而我们的NRI模型则使用离散的潜在变量(z)来表示对象之间的交互类型。为了能够在反向传播过程中优化离散的潜在变量,我们采用了连续的松弛方法,如Gumbel-Softmax或Straight-Through(ST)估计器,以便能够利用重参数化技巧进行梯度传播。这种方法允许我们在保持潜在变量离散性的同时,有效地优化模型参数。 -
未建模的初始状态:
在原始的VAE中,通常会对整个数据序列(包括初始状态)进行建模。然而,在我们的NRI模型中,我们主要关注于对象之间的动态交互和这些交互如何影响对象的轨迹。因此,我们没有对初始状态的概率(p(x^1))进行显式建模。尽管如此,如果需要,我们可以轻松地扩展模型以包含对初始状态的建模,但这通常不会显著影响模型在动态和交互预测方面的性能。 -
图神经网络(GNN)的引入:
除了上述差异外,我们的NRI模型还引入了图神经网络(GNN)来捕捉对象之间的交互。GNN能够处理图结构的数据,并通过在节点和边之间传递信息来更新节点的表示。在我们的模型中,GNN被用作解码器的一部分,它根据潜在交互图(z)和历史轨迹来预测未来的轨迹。这种图结构的数据处理方法使得我们的模型能够更好地捕捉对象之间的复杂交互和依赖关系。
NRI模型通过引入多时间步预测、离散潜在变量与连续松弛、以及图神经网络等方法,在保持原始VAE框架灵活性的同时,针对动态系统和交互推理问题进行了有效的改进和优化。
模型的概览图如图 1 所示。接下来,我们将详细介绍模型的编码器和解码器部分。
 图 1. NRI模型由两个共同训练的部分构成:一个编码器,它根据输入轨迹预测潜在交互的概率分布 q ( z ∣ x ) q(z|x) q(z∣x);以及一个解码器,它根据编码器的潜在编码和轨迹的前一时间步生成轨迹预测。编码器采用具有多轮节点到边(v → e)和边到节点(e → v)消息传递的GNN形式,而解码器则并行运行多个GNN,每个GNN对应编码器潜在编码 q ( z ∣ x ) q(z|x) q(z∣x)提供的一种边类型。(图引用自论文:Neural Relational Inference for Interacting Systems
图 1. NRI模型由两个共同训练的部分构成:一个编码器,它根据输入轨迹预测潜在交互的概率分布 q ( z ∣ x ) q(z|x) q(z∣x);以及一个解码器,它根据编码器的潜在编码和轨迹的前一时间步生成轨迹预测。编码器采用具有多轮节点到边(v → e)和边到节点(e → v)消息传递的GNN形式,而解码器则并行运行多个GNN,每个GNN对应编码器潜在编码 q ( z ∣ x ) q(z|x) q(z∣x)提供的一种边类型。(图引用自论文:Neural Relational Inference for Interacting Systems
)
2.3.编码器
编码器在NRI模型中的核心任务是,在观察到轨迹数据 ( x = (x_1, \ldots, x_T) ) 的基础上,推断出对象间潜在的成对交互类型 ( z_{ij} )。由于真实世界的图结构通常是未知的,我们利用一个在全连接图(即每对对象之间都存在潜在的边)上运作的图神经网络(GNN)来预测这种潜在的图结构。
具体地,我们构建编码器模型如下:
q ( z i j ∣ x ) = softmax ( f enc ( x ) i j 1 : K ) q(z_{ij}|x) = \text{softmax}(f_{\text{enc}}(x)_{ij}^{1:K}) q(zij∣x)=softmax(fenc(x)ij1:K)
其中, f enc ( x ) f_{\text{enc}}(x) fenc(x) 是我们的编码器函数,它在一个不包含自环的全连接图上应用GNN操作。给定输入轨迹 x 1 , … , x T x_1, \ldots, x_T x1,…,xT,编码器执行以下消息传递操作来逐步构建对象的表示和边的嵌入:
-
初始化节点嵌入:
h j 1 = f emb ( x j ) h^1_j = f_{\text{emb}}(x_j) hj1=femb(xj)
这里, f emb f_{\text{emb}} femb 是一个嵌入函数,它将原始轨迹数据 ( x_j ) 映射到初始的节点表示 h j 1 h^1_j hj1。 -
边嵌入的第一层更新:
h ( i j ) 1 = f e 1 ( [ h i 1 , h j 1 ] ) h^1_{(ij)} = f^1_e([h^1_i, h^1_j]) h(ij)1=fe1([hi1,hj1])
对于每对节点 ( i , j ) (i, j) (i,j), f e 1 f^1_e fe1 是一个边更新函数,它接受两个相邻节点的嵌入 h i 1 h^1_i hi1 和 h j 1 h^1_j hj1,并输出一个更新的边嵌入 h ( i j ) 1 h^1_{(ij)} h(ij)1。 -
节点嵌入的第二层更新:
h j 2 = f v 1 ( ∑ i ≠ j h ( i j ) 1 ) h^2_j = f^1_v\left(\sum_{i \neq j} h^1_{(ij)}\right) hj2=fv1 i=j∑h(ij)1
这里, f v 1 f^1_v fv1 是一个节点更新函数,它聚合所有指向节点 j j j 的边嵌入 h ( i j ) 1 h^1_{(ij)} h(ij)1,并据此更新节点 j j j 的嵌入 h j 2 h^2_j hj2。 -
边嵌入的第二层更新(可选):
h ( i j ) 2 = f e 2 ( [ h i 2 , h j 2 ] ) h^2_{(ij)} = f^2_e([h^2_i, h^2_j])