Verifieable FHE（VFHE）：使用Plonky2来证明Zama TFHE的“Bootstrapping的正确执行”

news2024/9/20 7:46:12

1. 引言

Zama团队2024年论文Towards Verifiable FHE in Practice: Proving Correct Execution of TFHE’s Bootstrapping using plonky2 中：

  • 首次阐述了，在实践中，将整个FHE bootstrapping操作，使用SNARK来证明。
  • 在其相应的https://github.com/zama-ai/verifiable-fhe-paper（Rust，Plonky2）开源代码实现中，为该bootstrapping操作设计了算术电路，并使用Plonky2进行了证明：
    • 在保证功能完整和安全的情况下，对TFHE的programmable bootstrapping中的操作进行了少量调整，使其能在算术电路中更高效地表示。
    • 在AWS C6i.metal实例上，证明该电路用时20分钟。
    • proof size约为200kB。
    • 验证该proof用时少于10ms。
    • 为实现memory-efficient，利用了（bootstrapping操作）该计算的结构化优势，以及，Plonky2的递归IVC能力，实现了递归证明。

Fully Homomorphic Encryption (FHE) 全同态加密技术：

  • 支持对密文输入做任意计算，生成密文输出。
  • 对密文输出解密的结果，等于，直接对明文输入做相应计算的结果。

Succinct Non-interactive ARguments of Knowledge (SNARKs) 密码学技术：

  • 支持Prover，让Verifier信服，某任意计算执行正确。【数据必须是明文的】

FHE和SNARKs各有所短：

  • FHE自身无法保证该计算的正确性，因此也无法提供任何计算完整性保证，使得在真实世界的FHE部署时，存在可疑的隐私攻击问题。
  • SNARKs可保证计算完整性，但需要知悉数据的明文信息，来证明基于这些数据的计算是正确的，对于某些特定隐私保护应用场景，是命令禁止提供数据明文信息的。

FHE和SNARKs相结合：

  • 可获得verifiable FHE（VFHE）：支持Prover，让Verifier信服，基于密文数据的任意计算执行正确。

VFHE的迷人之处在于，可将该技术用于如下场景：

  • 改进区块链协议，以支持私有交易。
  • 解决计算外包中的安全问题，可用于替换安全硬件模块，将对硬件厂商的信任，转移至，对密码学假设的信任。

尽管这在理论上听起来不错，但实践中的核心问题在于：

  • 相比于明文运算，FHE会引入大量的开销。
  • 相比于待证明的计算本身，SNARKs Prover计算量要贵得多。

因此，核心在于：

  • 如何让VFHE具备实用性

经典FHE方案包括：

  • 1）密文操作：对明文的同态运算。通常可高效计算，且可使用SNARK证明。
  • 2）bootstrapping操作：最昂贵的操作。

若不熟悉FHE，可能对bootstrapping操作不了解，详情可参看：

  • Zama团队2022年5月4日博客 TFHE Deep Dive - Part I - Ciphertext types

可简单将bootstrapping操作看成是：

  • 一种密文管理操作。
  • 支持某program基于密文数据做无限计算。

bootstrapping操作通常为FHE方案中最昂贵的操作，因此，实现真正实用VFHE系统的最大障碍在于：

  • bootstrapping操作。

因此，VFHE系统实用性的关键，在于：

  • 对于FHE真实参数（而不是toy参数），使用SNARK，高效证明bootstrapping，的能力。

基于此动机，Zama团队2024年研究并发布了论文Towards Verifiable FHE in Practice: Proving Correct Execution of TFHE’s Bootstrapping using plonky2 。

Zama团队专注于TFHE：

  • TFHE提供了非常轻量级的programmable bootstrapping (PBS)。

尽管TFHE的bootstrapping，比其它FHE方案中的bootstrapping，计算开销更低，但其也足够复杂，使得若直观对其做SNARK-ifying操作，将导致Prover需要巨大的内存，对大多数应用来说是不切实际的。

  • Zama团队曾实践过，使用FHE toy参数（不是真实参数），在具有128GB RAM的AWS实例上运行，直接内存溢出。

这就意味着，直接对TFHE的bootstrapping做SNARK-ifying操作，不是高效的方案。为此，Zama团队专注于利用bootstrapping操作中的结构化特性：

  • TFHE的PBS中，包含一个具有多次（约600到700次）迭代的循环
  • SNARKs技术可使用Incrementally Verifiable Computation（IVC） 来高效证明该循环，而不是将该循环展开为一个大的电路。所谓IVC，是指一次证明一个迭代，而不是一次证明所有迭代。

Zama团队开源代码https://github.com/zama-ai/verifiable-fhe-paper（Rust，Plonky2）中，使用Plonky2实现了基于递归的IVC方案，并将该IVC方案用于了TFHE PBS。其中Plonky2支持非常高效的递归，适用于本场景。

  • 1）每次迭代中，会生成单个proof，该单个proof对应为：
    • 1.1）该次迭代的实际计算
    • 1.2）之前迭代的proof的verification
  • 2）在循环的最后一次迭代，所生成的final proof，可让Verifier信服，之前的中间态proof均是正确生成和验证通过的。

因此，可将传统PBS计算的循环操作，转换为统一算术电路格式——可使用IVC来证明该统一格式的算术电路。

Zama团队对其TFHE进行了少量调整，使其更适合于基于有限域的算术电路模型。如：

  • 将密文的modulus，修改为Plonky2原生使用的素数
  • 修改了key switch，使得可通过external product来执行

需要调整参数，但确保这些参数仍是正确的且是安全的（目标是128-bit安全性）。PBS的循环迭代电路，如下图所示：【其中忽略了检查之前迭代proof的verifier电路】
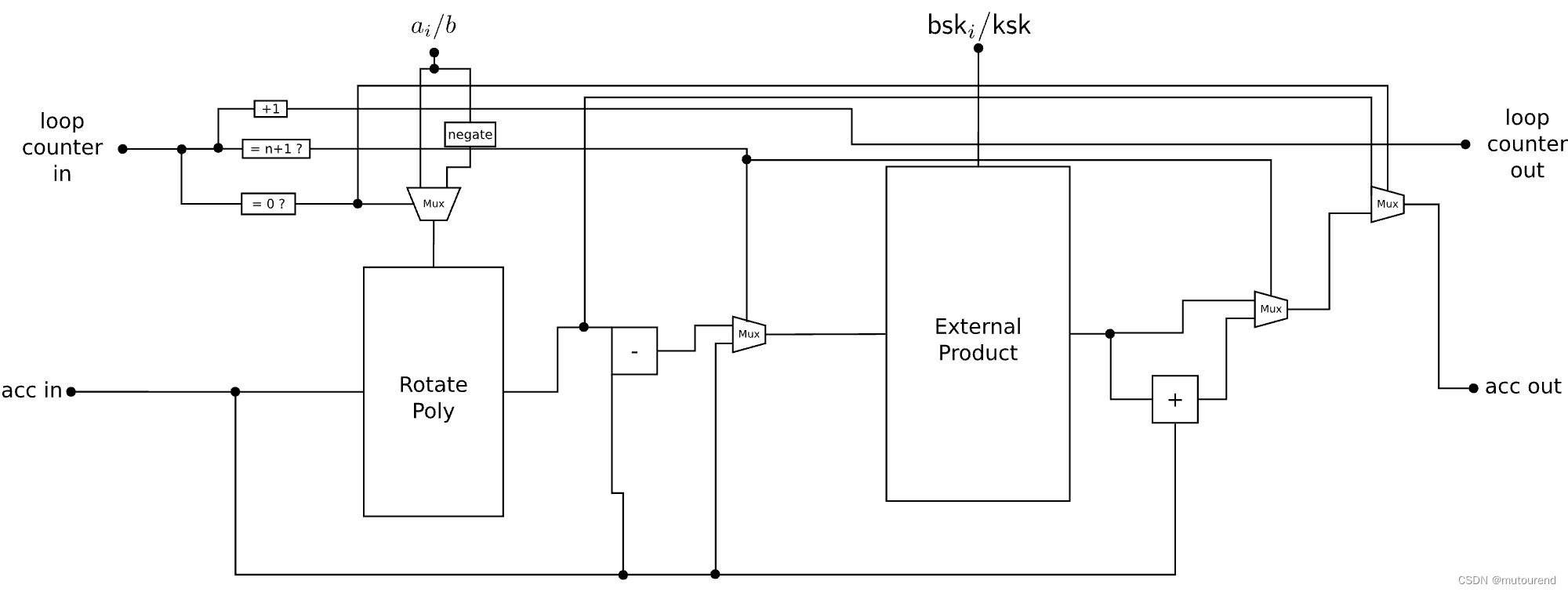
在这里插入图片描述
该电路会从前一迭代中接收loop counter n n n，以及前一迭代的结果，作为输入。该loop counter n n n值，决定了对前一迭代结果应用什么函数。该函数：

  • 要么为：简单的negacyclic polynomial rotation (“Rotate Poly”)
  • 要么为：在该input及其negacyclic rotation 之间有一个密文multiplexer（“Rotate Poly” + “External Product”）
  • 要么为：某key switching操作（通过“External Product”）。

该PBS中包含了以上3种操作。其中：

  • 对negacyclic polynomial rotation (“Rotate Poly”) 的子电路，以及，对external product的子电路，支配了整个电路size，从而支配了Prover开销。

详细的实现，可参看论文Towards Verifiable FHE in Practice: Proving Correct Execution of TFHE’s Bootstrapping using plonky2。

借助基于IVC的实现，所需内存量降了一个量级，使得消费级笔记本也可运行该Prover。在经典AWS示例中，计算proof需约20分钟，仍相对较长，但已接近实用水平了。

SystemProver Time (min)Verifier Time (ms)
M2 MacBook Pro - 8 cores, 24GB485
Hpc7a.96xlarge - 192 cores, 768GB188

同时，Zama团队将其Plonky2 IVC实现，与通用zkVMs（RISC0和SP1）对比发现，Zama团队的IVC方案性能要高2个数量级。

因此，Zama团队认为：

  • VFHE处于实用化的边缘。
  • 证明FHE方案中最困难部分（bootstrapping），可使用具有非常合理计算资源的SNARK来证明。
  • 这是一个重要的里程碑，也是一个开始。
  • 仍有许多途径待探索，如：
    • 如何将Prover，由PBS电路，扩展到，完整的FHE电路？
    • 是否有改进基于通用zkVM的实现的技术？是否有更适合FHE的zkVM？
    • 使用基于folding的IVC（如见2024年论文Mangrove: A Scalable Framework for Folding-based SNARKs），而不是基于递归的IVC，能否获得更好的效果？
  • 坚信VFHE方案将对隐私技术产生巨大影响，并将解锁众多惠及所有人的应用程序。

对于https://github.com/zama-ai/verifiable-fhe-paper（Rust，Plonky2）开源代码，取N=8，cargo test，有：

running 22 tests
max error: 0.00000007958257409723952
s_lwe: [1]
test vtfhe::crypto::poly::tests::test_ntt ... ok
test vtfhe::crypto::glwe::tests::test_partial_key ... ok
test vtfhe::crypto::glwe::tests::test_glwe_ct ... ok
error 1: 0.000018930169723786925
error 2: 0.000005441306717476589
error out: 0.9999756285235587
test vtfhe::crypto::lwe::tests::test_lwe_ct ... ok
testv: Poly { coeffs: [0, 1, 2, 3, 4, 5, 6, 7] }
message: 1152921504338411520 * 5 = 5764607521692057600
[13386287096109278436, 704150548386751715]
lwe key: [1, 0]
init acc: Poly { coeffs: [0, 1, 2, 3, 4, 5, 6, 7] }
m: 7, -Delta * m: 10376293539045703681
lwe_ct: [17476228523215945199, 15041682749057372911, 7099934984170241518]
test vec_arithmetic::tests::test_vec_add ... ok
test vtfhe::glwe_poly::tests::test_poly_const_rotate ... ok
test vtfhe::tests::test_glwe_select ... ok
test vec_arithmetic::tests::test_vec_mul ... ok
test vec_arithmetic::tests::test_vec_add_many ... ok
test vec_arithmetic::tests::test_vec_inner ... ok
test ntt::tests::test_ntt_backward ... ok
test vtfhe::tests::test_poly_rotate ... ok
test ntt::tests::test_ntt_forward ... ok
9223372040287211088 decomposed is [79, 18446744069414584271, 18446744069414584216, 18446744069414584270, 2, 0, 0, 18446744069414584193]
test vtfhe::glwe_poly::tests::test_decompose ... ok
test vtfhe::glwe_poly::tests::test_vec_decompose ... ok
test vtfhe::tests::test_key_switch ... ok
test vtfhe::glev_ct::tests::test_glev_mul ... ok
a: 1265430409327377521
m_in: Poly { coeffs: [0, 1, 2, 3, 4, 5, 6, 7] }
m_out: Poly { coeffs: [18446744069414584314, 0, 1, 2, 3, 4, 5, 6] }
test vtfhe::tests::test_blind_rot_step ... ok
test vtfhe::ggsw_ct::tests::test_external_product ... ok
test vtfhe::ggsw_ct::tests::test_key_switch ... ok
test vtfhe::tests::test_blind_rot ... ok

thread 'vtfhe::ivc_based_vpbs::tests::test_ivc_blind_rot' panicked at src/vtfhe/crypto/poly.rs:167:34:
attempt to subtract with overflow
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace
test vtfhe::ivc_based_vpbs::tests::test_ivc_blind_rot ... FAILED

failures:

failures:
    vtfhe::ivc_based_vpbs::tests::test_ivc_blind_rot

test result: FAILED. 21 passed; 1 failed; 0 ignored; 0 measured; 0 filtered out; finished in 18.30s

参考资料

[1] Zama团队2024年5月5日博客 Verifiable FHE Bootstrapping using SNARKs
[2] Zama团队2024年论文Towards Verifiable FHE in Practice: Proving Correct Execution of TFHE’s Bootstrapping using plonky2

FHE系列博客

  • 技术探秘：在RISC Zero中验证FHE——由隐藏到证明：FHE验证的ZK路径（1）
  • 基于[Discretized] Torus的全同态加密指引（1）
  • 基于[Discretized] Torus的全同态加密指引（2）
  • TFHE——基于[Discretized] Torus的全同态加密 代码解析
  • 技术探秘：在RISC Zero中验证FHE——RISC Zero应用的DevOps（2）
  • FHE简介
  • Zama TFHE-rs
  • Zama TFHE-rs白皮书（1）
  • Zama TFHE-rs白皮书（2）
  • ZK系统内隐私 VS. FHE系统内隐私
  • ZK vs FHE
  • FHE全同态加密简介
  • FHE与TEEs区别：Downfall攻击
  • Greco：使用ZKP来证明FHE参与方的RLWE密文格式正确
  • FHE入门

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1860374.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

买卖的价差与速率之间建立的关系

买卖的价差与速率之间建立的关系

import numpy as np import matplotlib.pyplot as plt# 参数设置 A 100 delta_ba np.array([1, 5, 10]) # 时间差，以秒为单位 k_values [0.05, 0.1, 0.01] # 不同的k值# 计算不同k值下的λb,a def calculate_lambda(A, k, delta):return A * np.exp(-k * delta…
阅读更多...
NSSCTF-Web题目16

NSSCTF-Web题目16

目录 [GDOUCTF 2023]受不了一点 1、题目 2、知识点 3、思路 [UUCTF 2022 新生赛]ez_upload 1、题目 2、知识点 3、思路 [GDOUCTF 2023]受不了一点 1、题目 2、知识点 php代码审计、数组绕过、弱比较绕过 3、思路 打开题目，出现代码，我们进行代…
阅读更多...
AIGC已经火了好几年，现在学还抓得住这个风口吗？

AIGC已经火了好几年，现在学还抓得住这个风口吗？

简介 进入人工智能（AI）与游戏行业整合（AIGC）领域需要考虑当前的市场需求和行业发展阶段： 1、市场需求：目前，人工智能和游戏行业都在不断发展壮大，并且两者的结合也逐渐成为一个热门领…
阅读更多...
当前周周报自动生成工具

当前周周报自动生成工具

周报自动生成工具使用指南 功能简介 每次只用在xx周报.xlsx 中进行工作内容的更改，然后写完之后点一下run\_clear\_formulas\_and\_save.bat就能导出一份当前周周报，不用进行每周都自己新建一份然后把所有需要改时间的地方都改一遍这种重复劳动。 自动…
阅读更多...
C++三大特性之一：多态

C++三大特性之一：多态

一、多态 1、通过指针创建对象&#xff08;动态分配&#xff09; #include <iostream> using namespace std;class Base { public:virtual void show() {cout << "Base class show" << endl;} };class Derived : public Base { public:void show…
阅读更多...
Android 13 修改系统导航默认值

Android 13 修改系统导航默认值

Android 13 原生系统上&#xff0c;设置-系统-手势-系统导航 菜单&#xff0c;可以修改系统导航方式。 手势导航&#xff1a; 三按钮导航&#xff1a; adb 获取当前导航方式&#xff0c;手势导航 是 2 &#xff0c;三按钮导航是 0 。 settings get secure navigation_mode 修…
阅读更多...
游戏AI的创造思路-技术基础-深度学习（2）

游戏AI的创造思路-技术基础-深度学习（2）

感觉坑越挖越大&#xff0c;慢慢填~~~~ 继续上篇进行填坑&#xff0c;这一篇我们介绍下循环神经网络 目录 3.2. 循环神经网络&#xff08;RNN&#xff09; 3.2.1. 算法形成过程 3.2.2. 运行原理 3.2.3. RNN有哪些优缺点 3.2.4. RNN参数 3.2.5. 如何选择RNN模型参数 3.2…
阅读更多...
odoo17 tree视图添加按钮

odoo17 tree视图添加按钮

需求描述 点击下图中tree视图上的同步退货单按钮&#xff0c;弹出相应的form视图进行退货单同步&#xff0c;然后点击同步按钮调用后端python代码处理。 实现步骤 主要文件目录结构 js文件的创建 /** odoo-module **/ import { registry } from "web/core/registry&quo…
阅读更多...
芒果YOLOv10改进66：特征融合Neck篇之原创 HFAMPAN 结构：信息高阶特征对齐融合和注入，全局融合多级特征，将全局信息注入更高级别

芒果YOLOv10改进66：特征融合Neck篇之原创 HFAMPAN 结构：信息高阶特征对齐融合和注入，全局融合多级特征，将全局信息注入更高级别

💡本篇内容：YOLOv10 改进原创 HFAMPAN 结构，信息高阶特征对齐融合和注入，全局融合多级特征，将全局信息注入更高级别 💡🚀🚀🚀本博客 改进源代码改进 适用于 YOLOv10 按步骤操作运行改进后的代码即可 💡本文提出改进 原创 方式：二次创新，YOLOv10 专属 论文…
阅读更多...
Spring Boot基础入门

Spring Boot基础入门

引言 Spring Boot是一个开源的Java框架&#xff0c;旨在简化Spring应用程序的创建和部署过程。它提供了一种快速和简便的方式来创建独立的、生产级别的基于Spring的应用程序。本文将介绍Spring Boot的基础知识&#xff0c;包括其核心特性、如何开始使用Spring Boot以及构建你的…
阅读更多...
Docker 安装和加速

Docker 安装和加速

目录 1.安装 2.了解 docker 信息 3.查询状态 4. 重新启动Docker 1.安装 yum install –y docker 2.了解 docker 信息 cat /etc/redhat-release 3.查询状态 systemctl status docker 4.支持 1.12 的 docker 镜像加速 sudo mkdir -p /etc/docker sudo tee /etc/docke…
阅读更多...
关于关闭防火墙后docker启动不了容器

关于关闭防火墙后docker启动不了容器

做项目的时候遇到个怪事&#xff0c;在Java客户端没办法操作redis集群。反复检查了是否运行&#xff0c;端口等一系列细节的操作&#xff0c;结果都不行。 根据提示可能是Linux的防火墙原因。于是去linux关闭了防火墙。 关闭后果不其然 可以操作reids了&#xff0c;可是没想到另…
阅读更多...
【linux学习十七】文件服务管理

【linux学习十七】文件服务管理

一、FTP FTP server:FTP(File Transfer Protocol,文件传输协议 )是 TCP/IP 协议组中的协议之一 软件包&#xff1a;vsftpd/安装 yum -y install vsftpd//准备文件 touch /var/ftp/abc.txt //注释:FTP服务器的主目录:“/var/ftp/”&#xff0c;是FTP程序分享内容的本机目录…
阅读更多...
ArkUI开发学习随机——得物卡片,京东登录界面

ArkUI开发学习随机——得物卡片,京东登录界面

案例一&#xff1a;得物卡片 代码&#xff1a; Column(){Column(){Image($r("app.media.mihoyo")).width(200).height(200)Row(){Text("今晚玩这个 | 每日游戏打卡").fontWeight(700).fontSize(16).padding(4)}.width(200)Text("No.12").fontWe…
阅读更多...
罗德与施瓦茨 ZND (RS) ZNB8 矢量网络分析仪

罗德与施瓦茨 ZND (RS) ZNB8 矢量网络分析仪

R&SZND 矢量网络分析仪 简介 R&S ZND 是一款提供最高 4.5 GHz 的单向测量的基本网络分析仪。 用户可选择选件以执行双向测量&#xff0c;并将频率范围扩展到 8.5 GHz。 主要特点 双端口网络分析仪&#xff0c;适用于 100 kHz 至 4.5 GHz 的单向测量 频率范围可扩展…
阅读更多...
一分钟扫盲：互联网产品B端，C端，G端都是啥，有什么特征。

一分钟扫盲：互联网产品B端，C端，G端都是啥，有什么特征。

在互联网产品中&#xff0c;B端、C端和G端是常用的分类方式&#xff0c;用于描述产品的目标用户群体和市场定位。 B端&#xff08;Business-to-Business&#xff09;&#xff1a; B端产品是面向企业或机构的产品&#xff0c;即企业与企业之间的交互和服务。B端产品的特点包括…
阅读更多...
​Python20 Numpy基础

​Python20 Numpy基础

NumPy&#xff08;Numerical Python&#xff09;是一个开源的Python库&#xff0c;广泛用于科学计算。它提供了一个高性能的多维数组对象&#xff0c;以及用于处理这些数组的工具和函数。NumPy是数据分析、机器学习、工程和科学研究中不可或缺的工具之一&#xff0c;因为它提供…
阅读更多...
Navicat连接Oracle出现Oracle library is not loaded的解决方法

Navicat连接Oracle出现Oracle library is not loaded的解决方法

目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 使用Navicat链接Oracle的时候，出现如下提示：Oracle library is not loaded. 截图如下所示： 2. 原理分析 通常是由于缺少必需的 Oracle 客户端库或环境变量未正确配置所致 还有一种情况是 32位与64位的不匹配：Navica…
阅读更多...
Labview_网络流

Labview_网络流

网络流的介绍 网络流是一种易于配置、紧密集成的动态通信方法&#xff0c;用于将数据从一个应用程序传输到另一个应用程序&#xff0c;其吞吐量和延迟特性可与 TCP 相媲美。但是&#xff0c;与 TCP 不同的是&#xff0c;网络流直接支持任意数据类型的传输&#xff0c;而无需先…
阅读更多...
一键设置水印，全面护航：跨境平台产品刊登新功能上线

一键设置水印，全面护航：跨境平台产品刊登新功能上线

一、Allegro、OZON、Coupang、Cdiscount、Wish、Temu、Walmart、OnBuy、TikTok、Wildberries平台新增产品刊登支持设置水印。 【普通水印】直接跳转到添加水印页面&#xff0c;勾选所要的图片&#xff0c;点击确定&#xff0c;自动替换原图。 【管理水印】直接跳转到水印模版页…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023